Содержание
- 2. Основные методы решения геометрических задач Метод дополнительных построений Метод геометрических преобразований Метод подобия Метод площадей Метод
- 3. Основные факторы успеха Время (чем больше времени на подготовку, тем лучше) Система (работа по плану, а
- 4. Причины ошибок в решении геометрических задач Незнание и/или непонимание аксиом, определений, теорем, а также методов решения
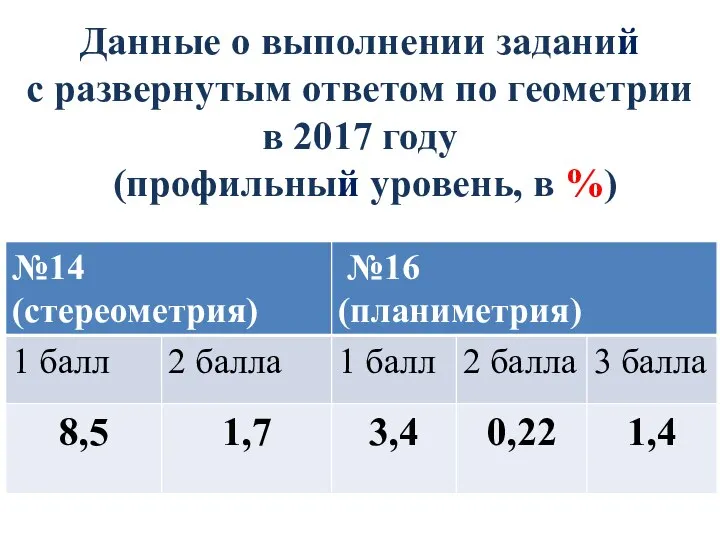
- 5. Данные о выполнении заданий с развернутым ответом по геометрии в 2017 году (профильный уровень, в %)
- 9. Что нужно знать Аксиомы и теоремы стереометрии и планиметрии Правила изображения (проектирования) пространственных фигур на плоскость
- 10. Что нужно уметь Применять знания в процессе решения задачи: Увидеть, что нужно построить на каждом шаге
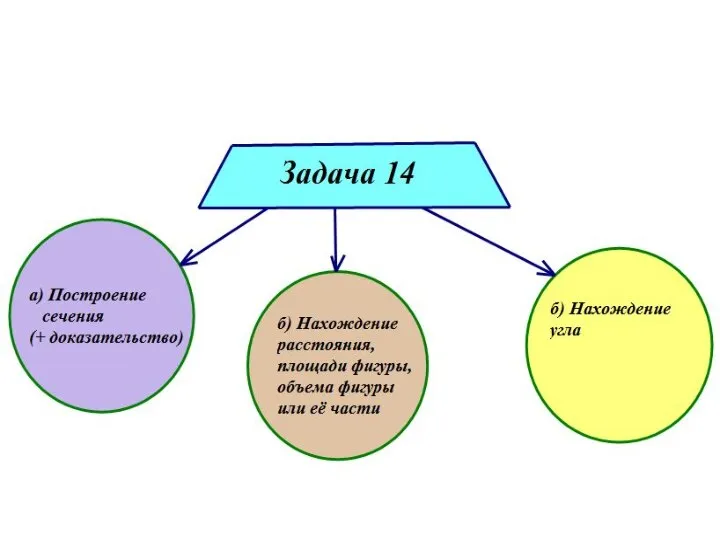
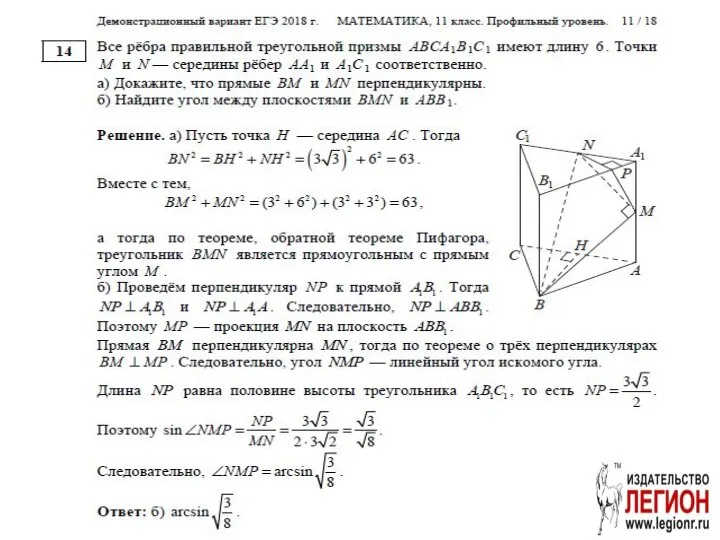
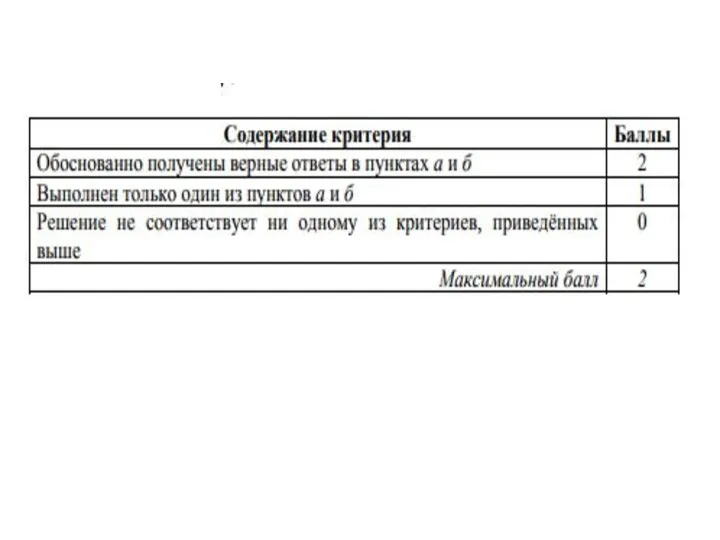
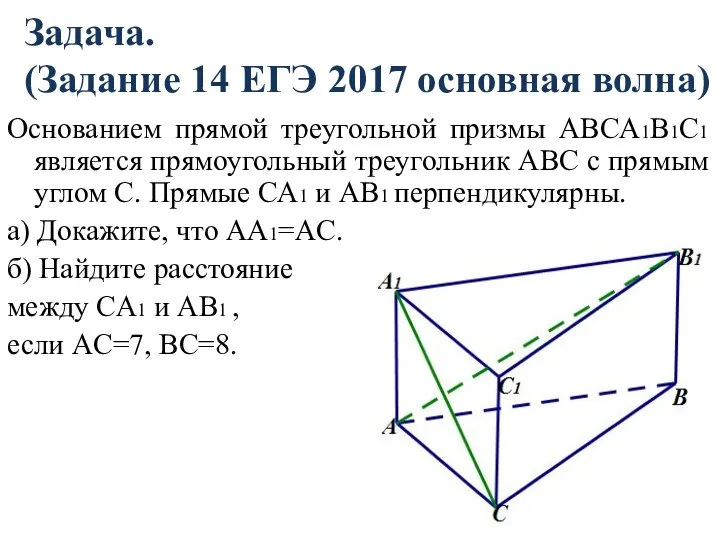
- 11. Задача. (Задание 14 ЕГЭ 2017 основная волна) Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC
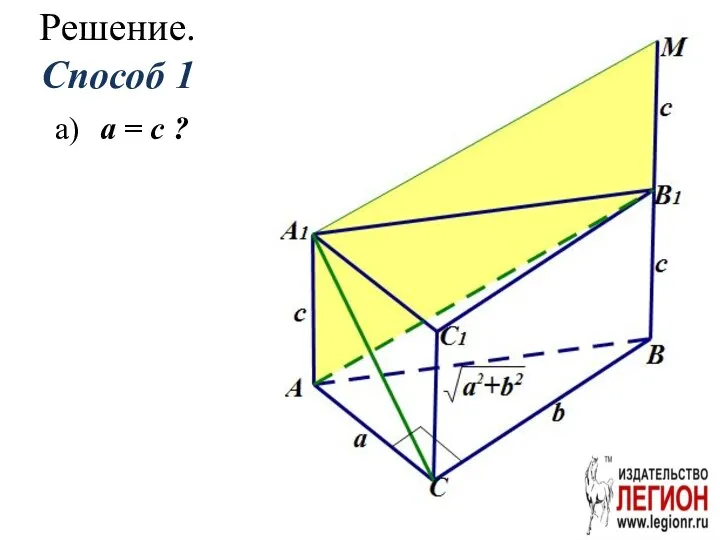
- 12. Решение. Способ 1 а) a = c ?
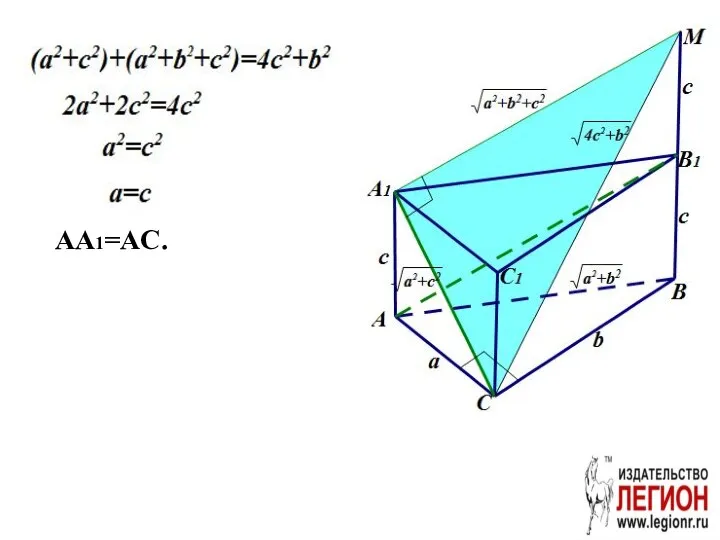
- 13. AA1=AC.
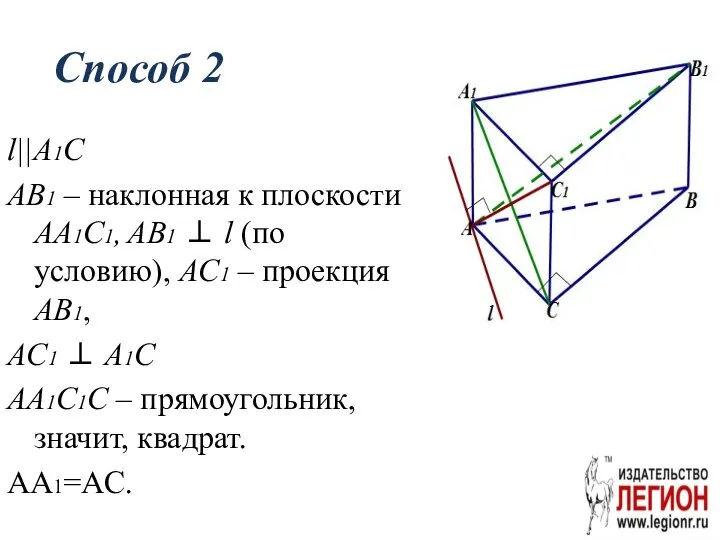
- 14. Способ 2 l||A1C AB1 – наклонная к плоскости AA1C1, AB1 ⊥ l (по условию), AC1 –
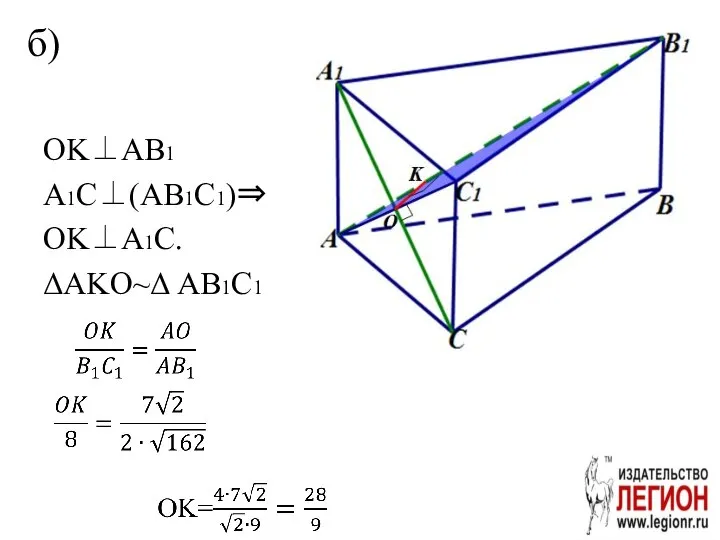
- 15. OK⊥AB1 A1C⊥(AB1C1)⇒ OK⊥A1C. ΔAKO~Δ AB1C1 б)
- 16. ρ(a,b)=ρ(A, α)
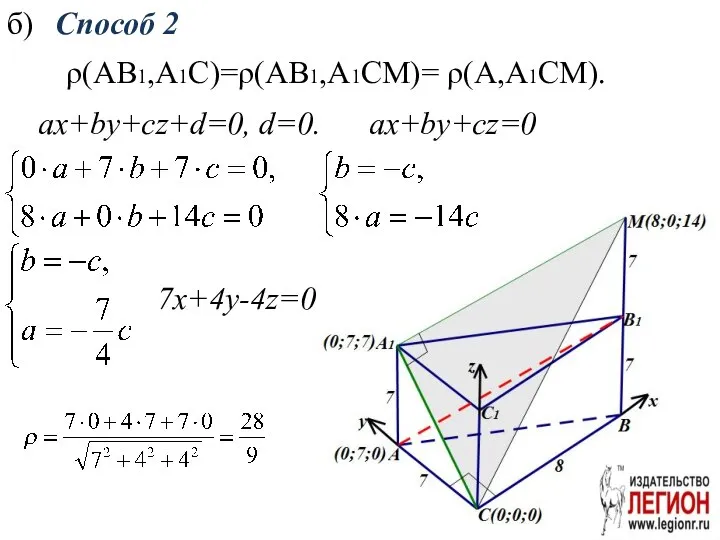
- 17. ρ(AB1,A1C)=ρ(AB1,A1CM)= ρ(A,A1CM). б) ax+by+cz+d=0, d=0. ax+by+cz=0 7x+4y-4z=0 Способ 2
- 18. Основные методы построения сечений многогранников Аксиоматический Метод следов Метод вспомогательных сечений (метод внутреннего проектирования) Комбинированный метод
- 19. Метод следов Понятие следа Линия пересечения плоскости сечения и плоскости грани многогранника называется следом секущей плоскости
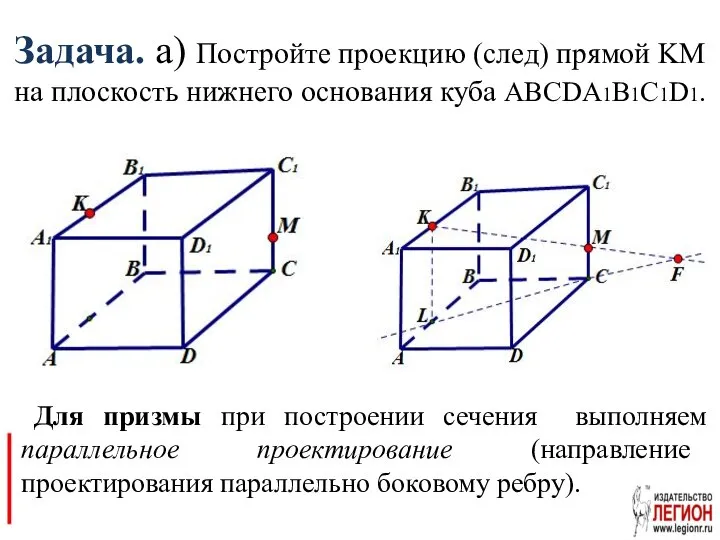
- 20. Задача. а) Постройте проекцию (след) прямой KM на плоскость нижнего основания куба ABCDA1B1C1D1. Для призмы при
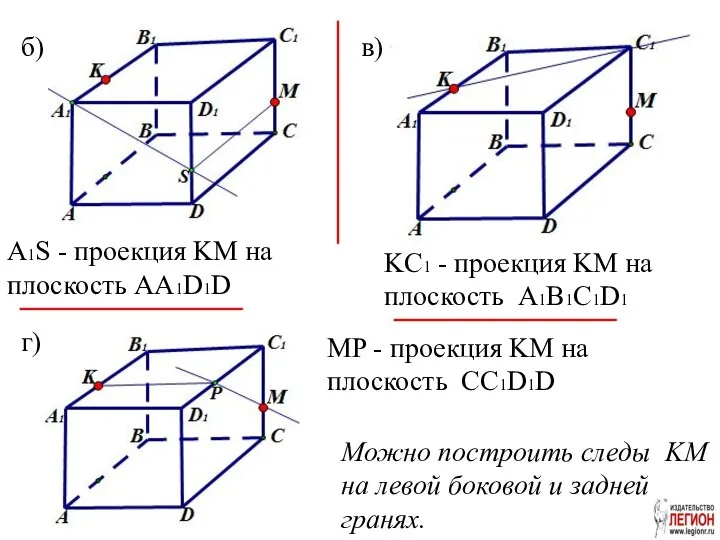
- 21. A1S - проекция KM на плоскость AA1D1D KC1 - проекция KM на плоскость A1B1C1D1 MP -
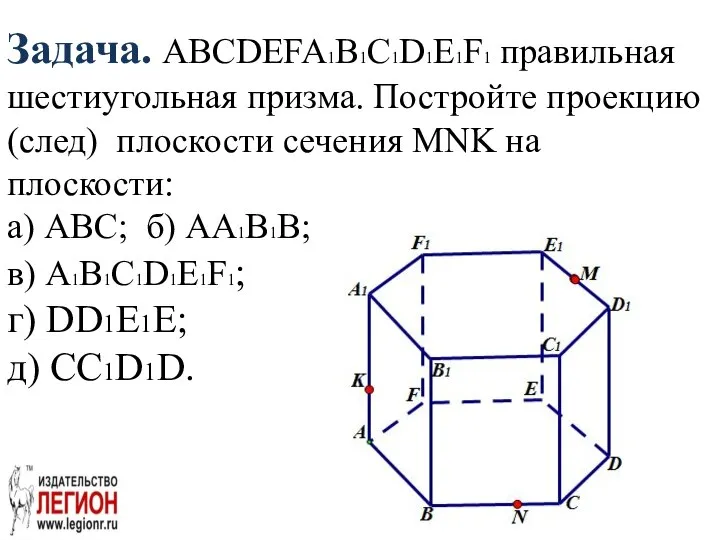
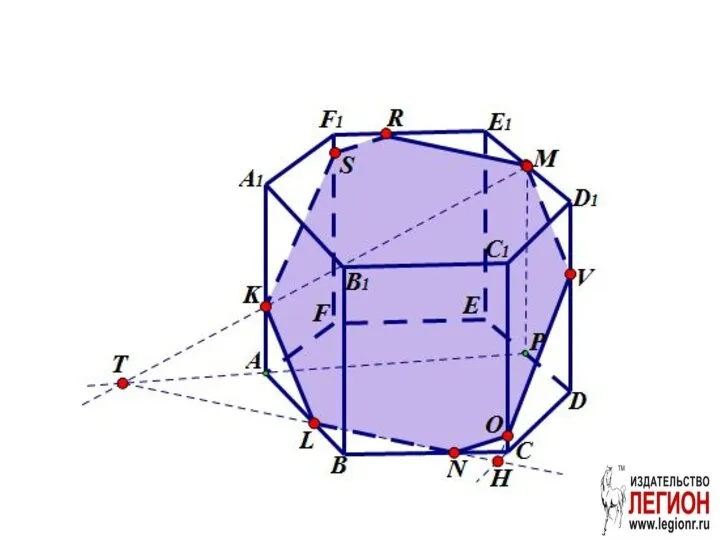
- 22. Задача. ABCDEFA1B1С1D1E1F1 правильная шестиугольная призма. Постройте проекцию (след) плоскости сечения MNK на плоскости: а) ABC; б)
- 23. а)
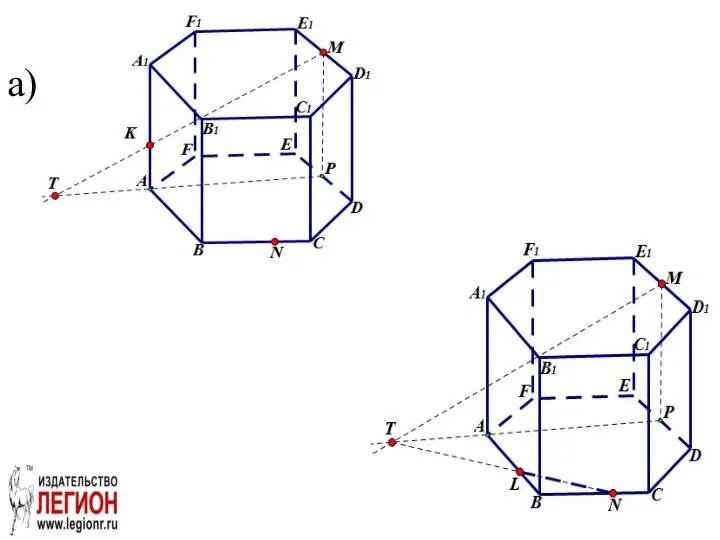
- 24. б) AA1B1B
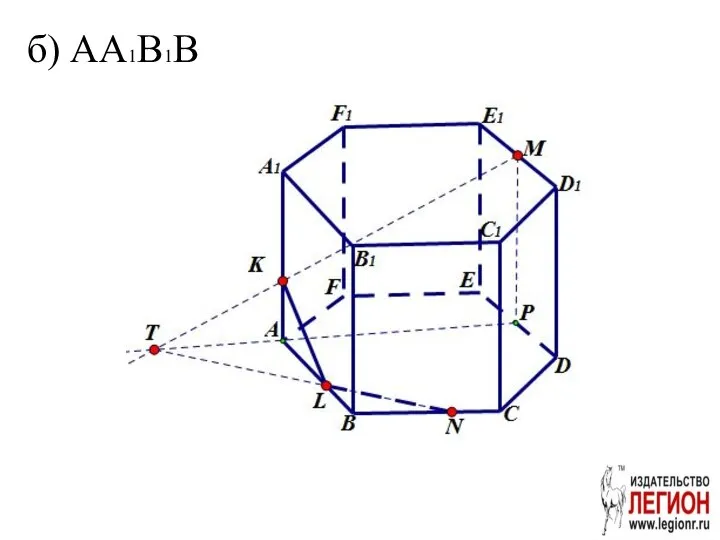
- 25. в) A1B1С1D1E1F1
- 26. Комбинированный метод Сочетание применения теорем о параллельности прямых и плоскостей в пространстве и аксиоматического метода.
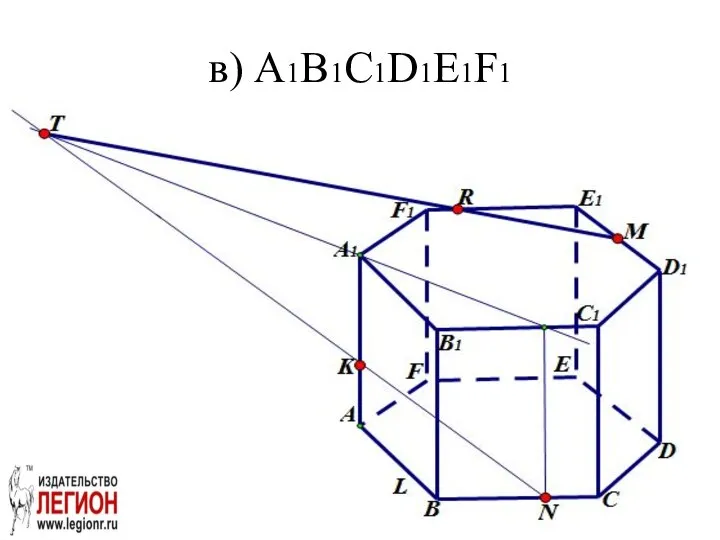
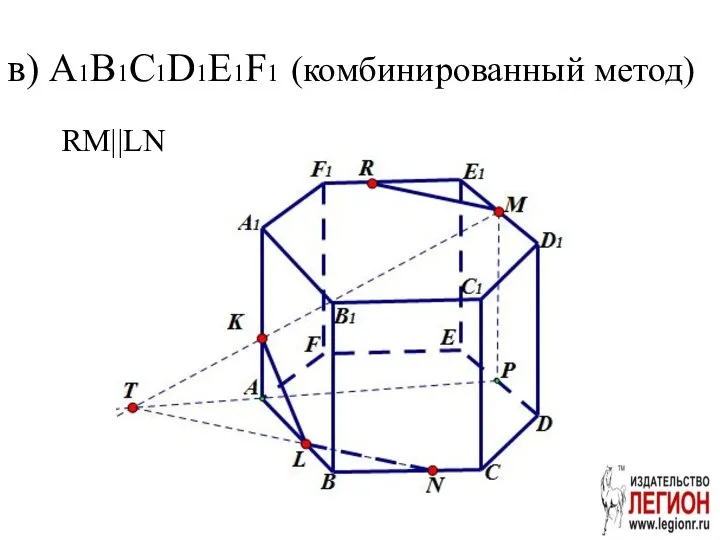
- 27. в) A1B1С1D1E1F1 (комбинированный метод) RM||LN
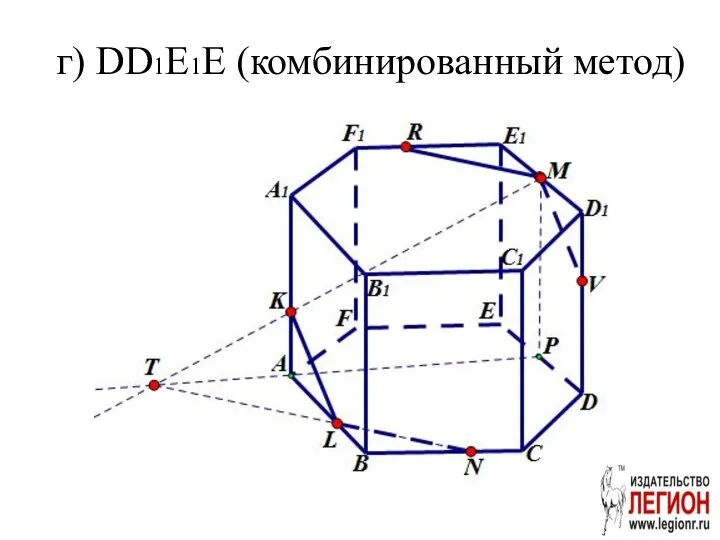
- 28. г) DD1E1E (комбинированный метод)
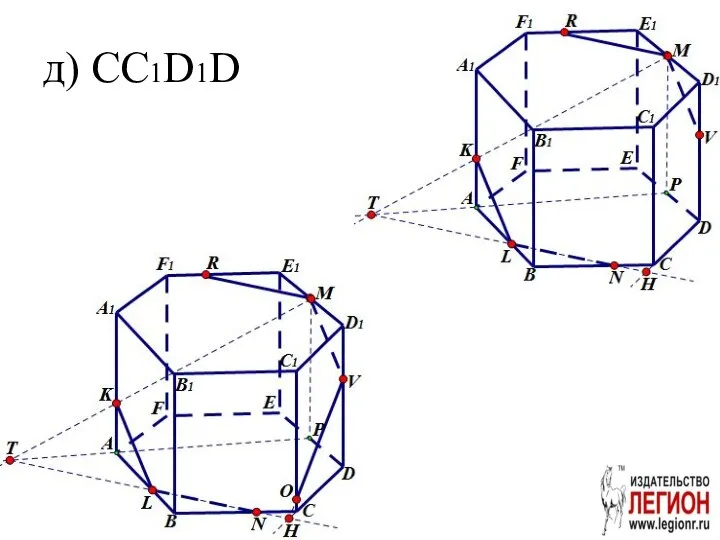
- 29. д) CC1D1D
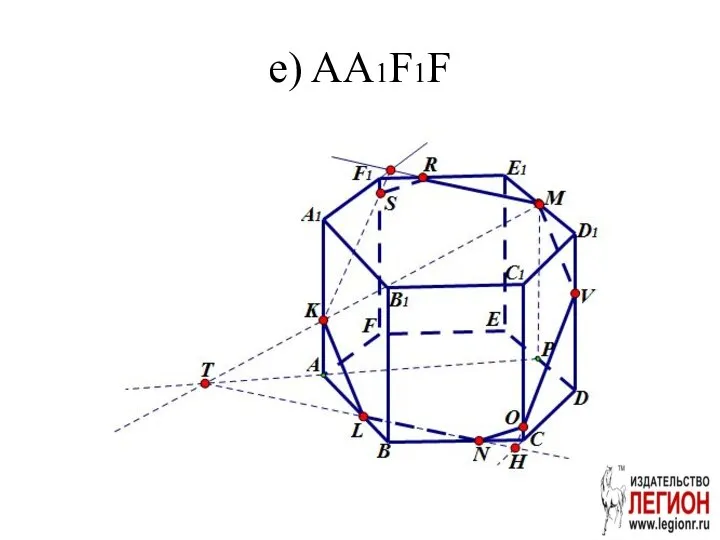
- 30. e) AA1F1F
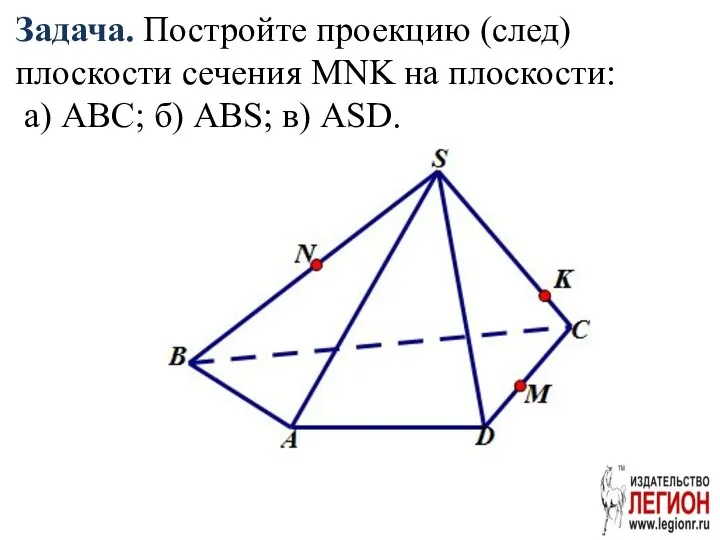
- 32. Задача. Постройте проекцию (след) плоскости сечения MNK на плоскости: а) ABC; б) ABS; в) ASD.
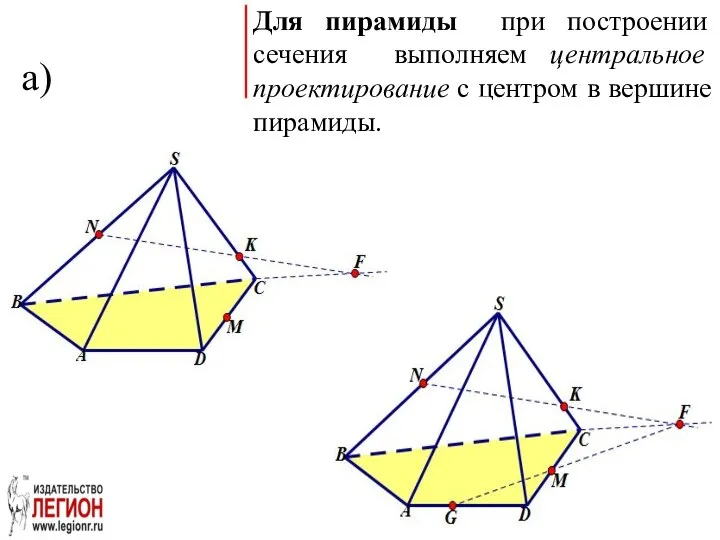
- 33. а) Для пирамиды при построении сечения выполняем центральное проектирование с центром в вершине пирамиды.
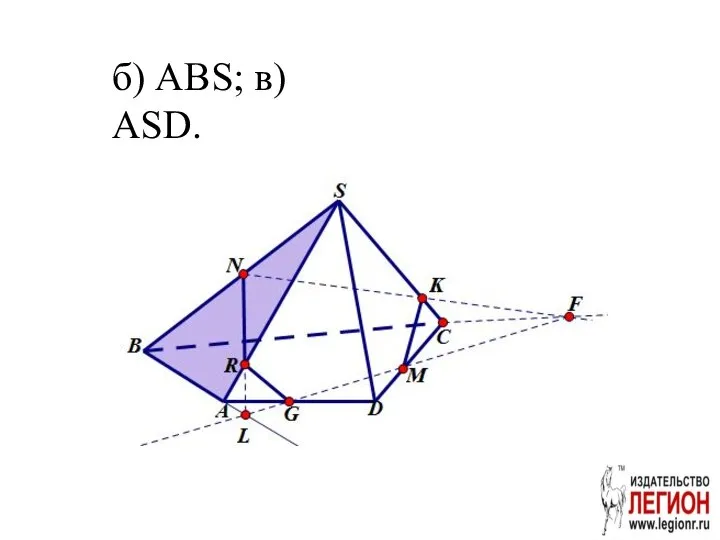
- 34. б) ABS; в) ASD.
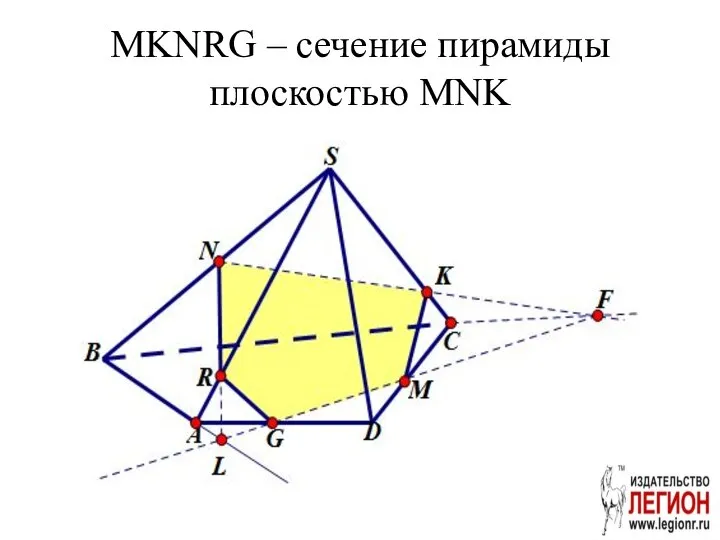
- 35. MKNRG – сечение пирамиды плоскостью MNK
- 36. Метод вспомогательных сечений (метод внутреннего проектирования) Универсальный метод, основанный на построении вспомогательных плоскостей, не выходящих за
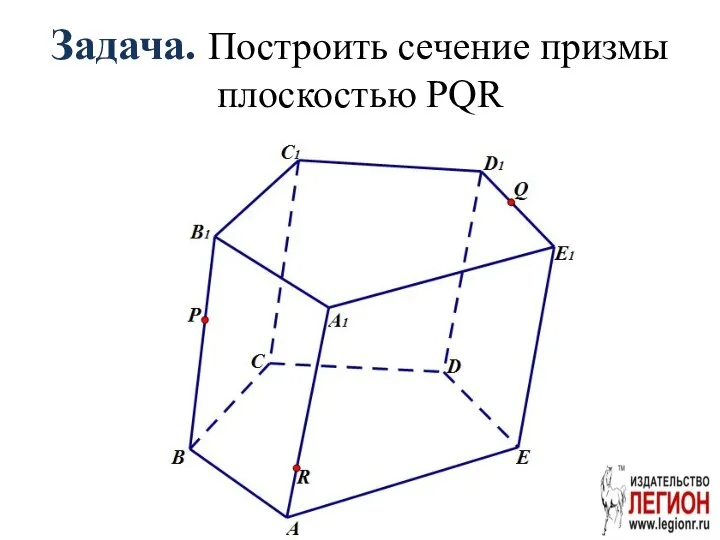
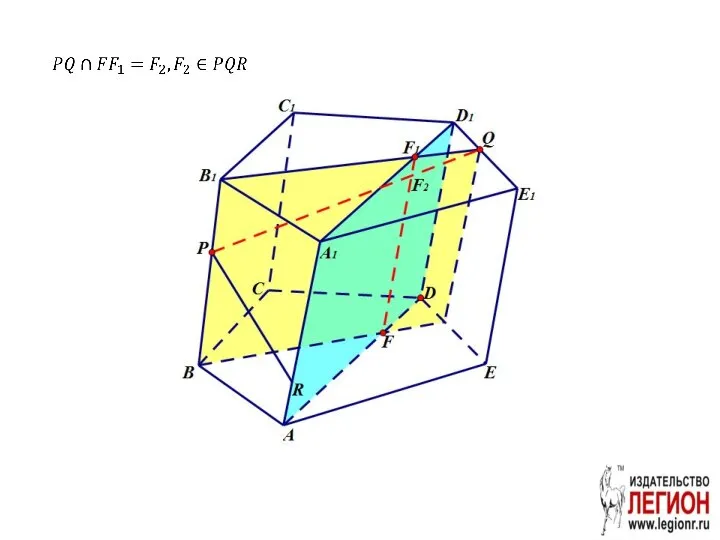
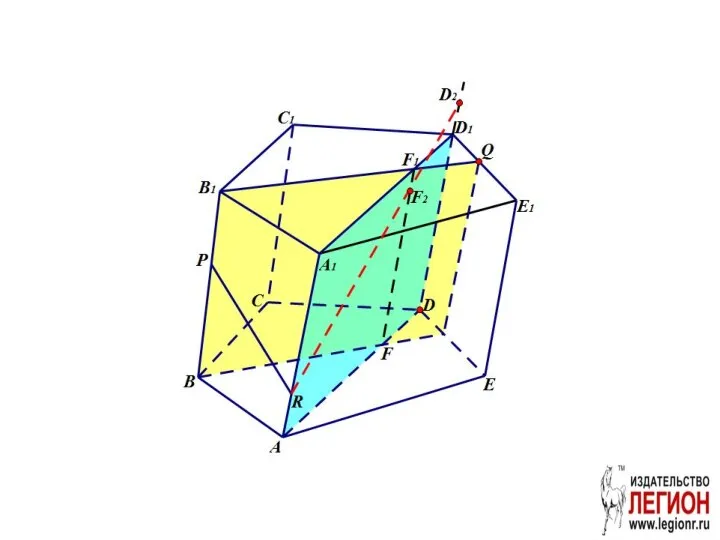
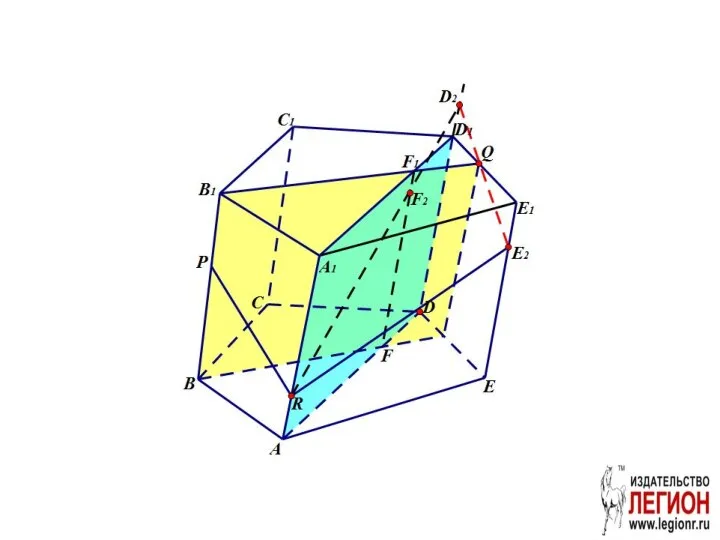
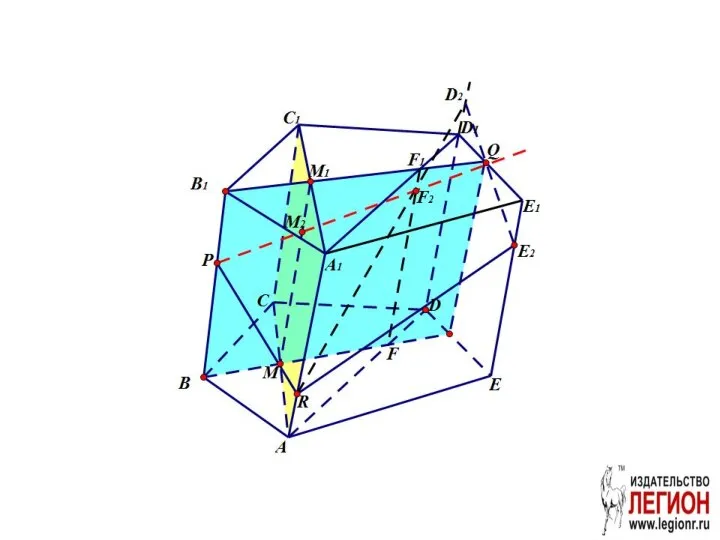
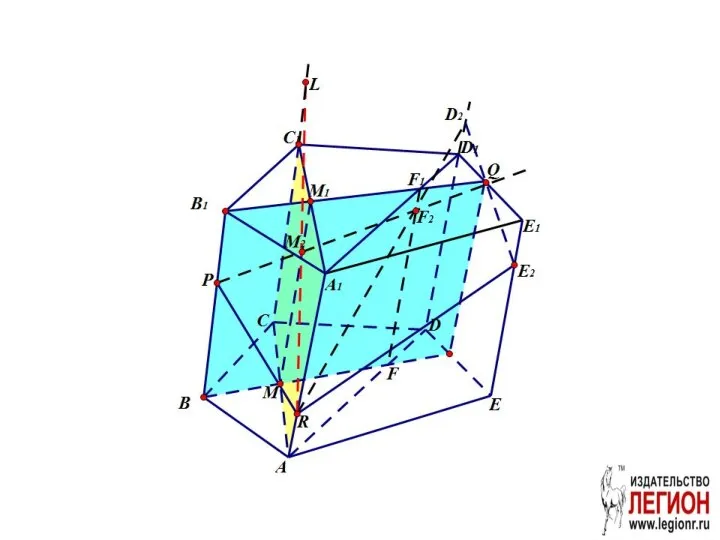
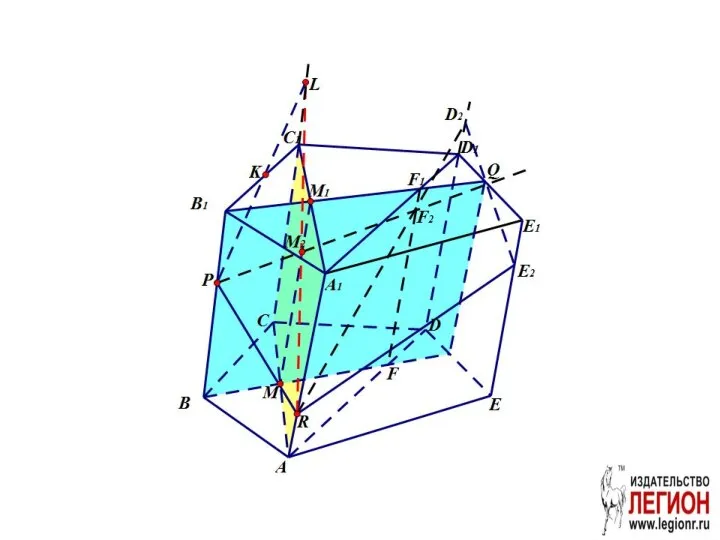
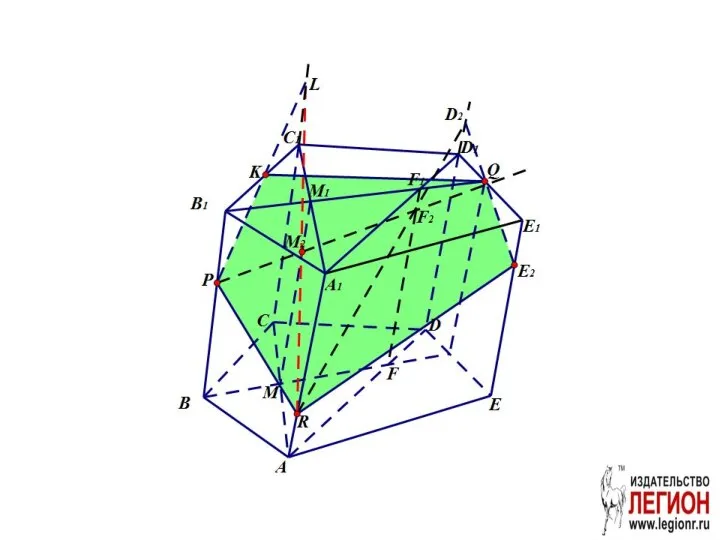
- 37. Задача. Построить сечение призмы плоскостью PQR
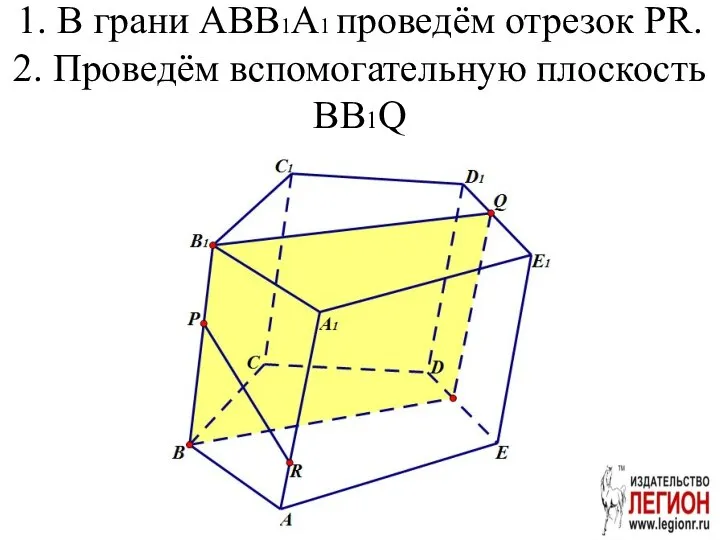
- 38. 1. В грани ABB1A1 проведём отрезок PR. 2. Проведём вспомогательную плоскость BB1Q
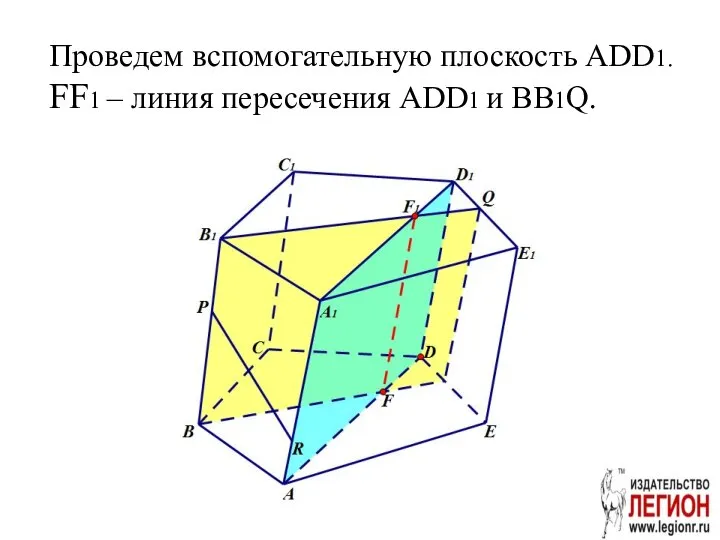
- 39. Проведем вспомогательную плоскость ADD1. FF1 – линия пересечения ADD1 и BB1Q.
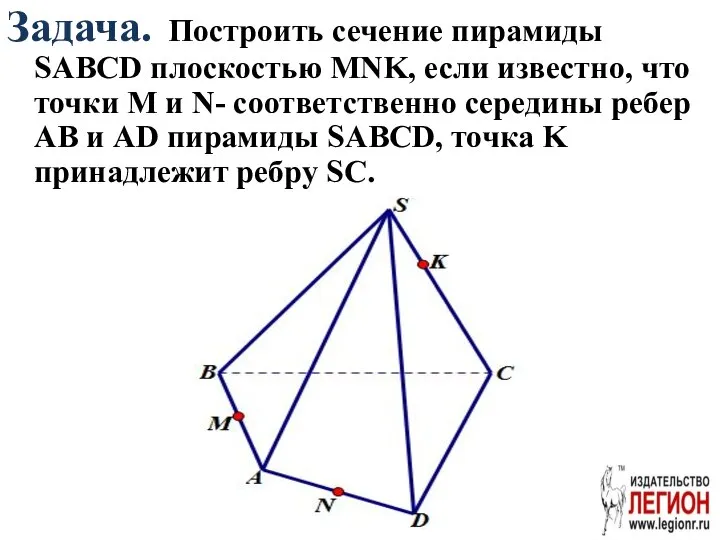
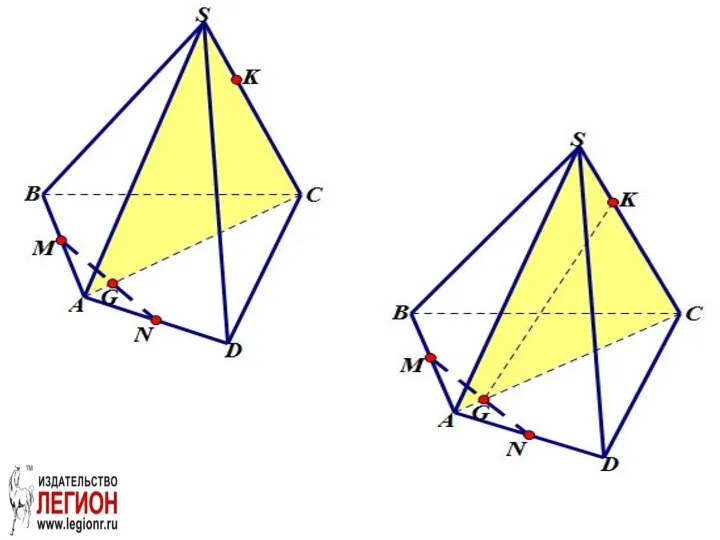
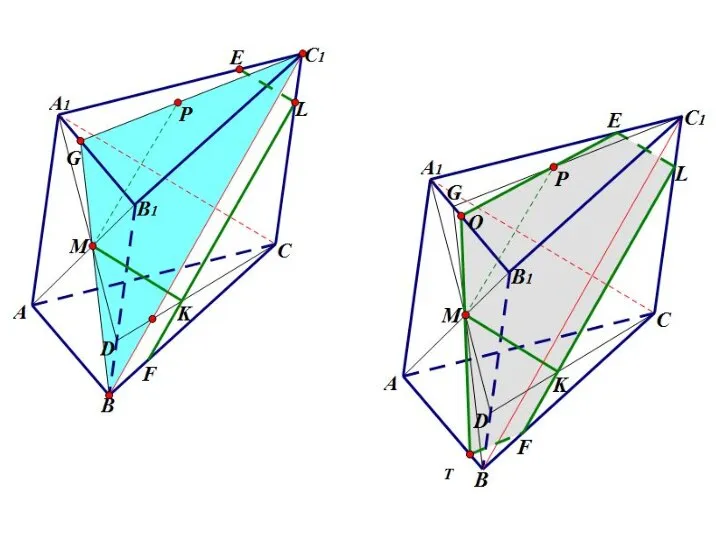
- 47. Задача. Построить сечение пирамиды SABCD плоскостью MNK, если известно, что точки M и N- соответственно середины
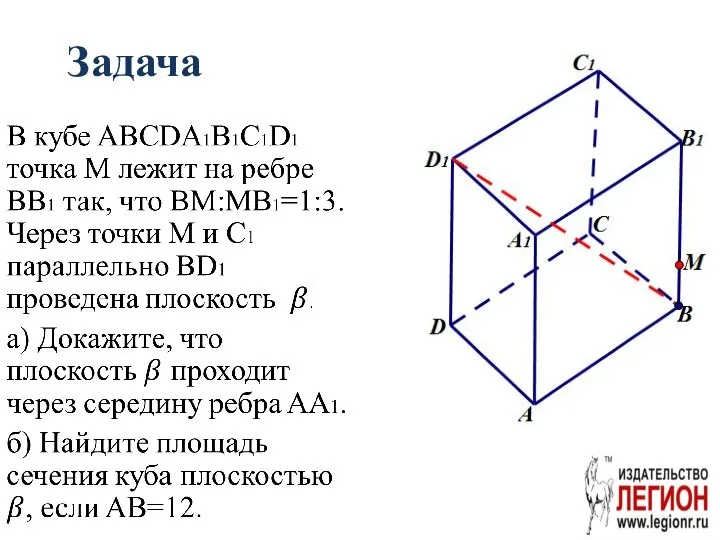
- 51. Задача
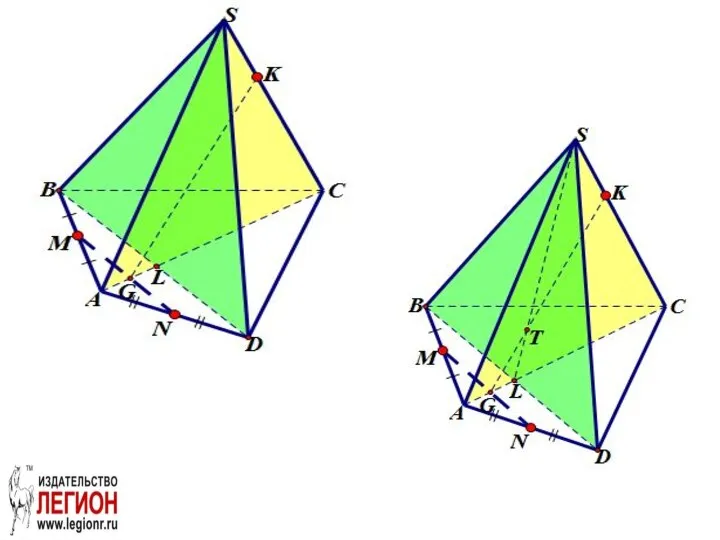
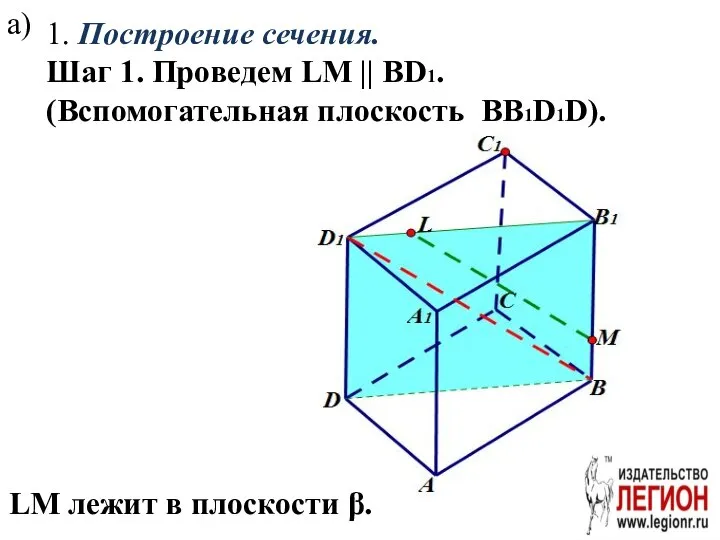
- 52. а) 1. Построение сечения. Шаг 1. Проведем LM || BD1. (Вспомогательная плоскость BB1D1D). LM лежит в
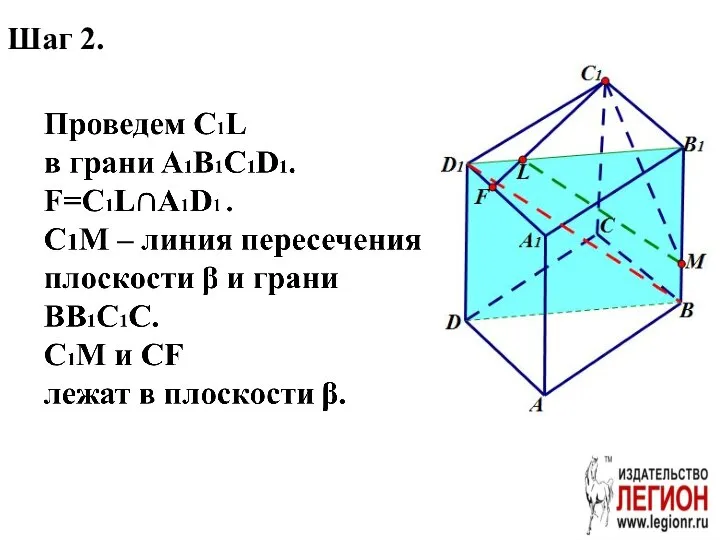
- 53. Шаг 2.
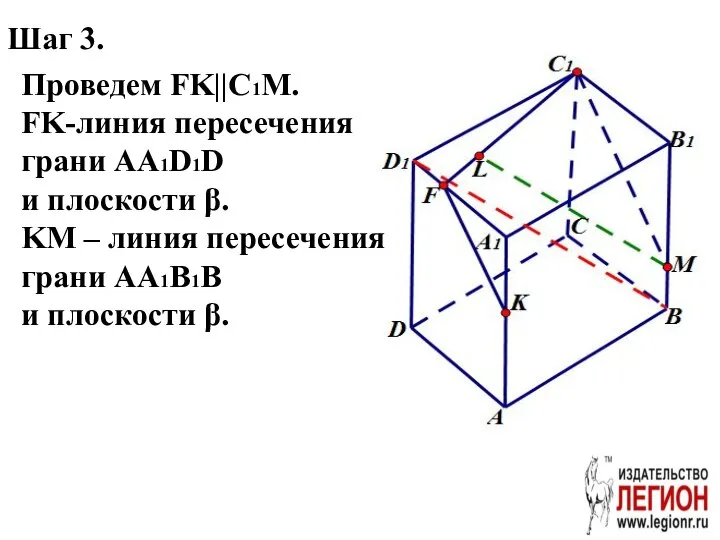
- 54. Шаг 3. Проведем FK||C1M. FK-линия пересечения грани AA1D1D и плоскости β. KM – линия пересечения грани
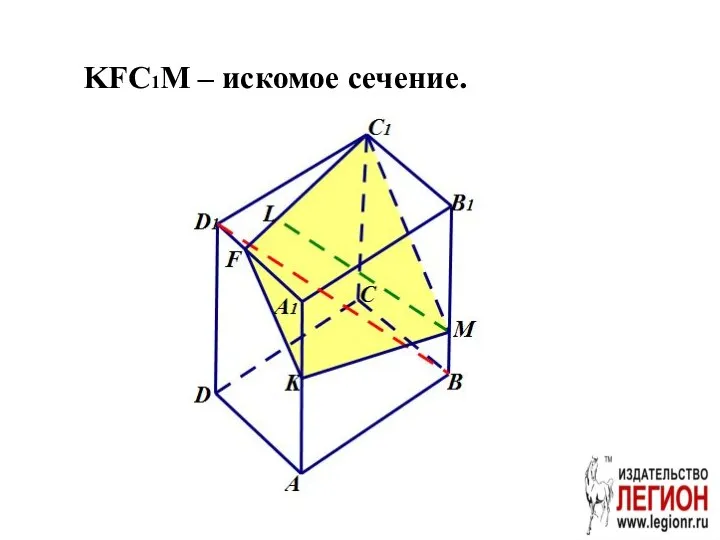
- 55. KFC1M – искомое сечение.
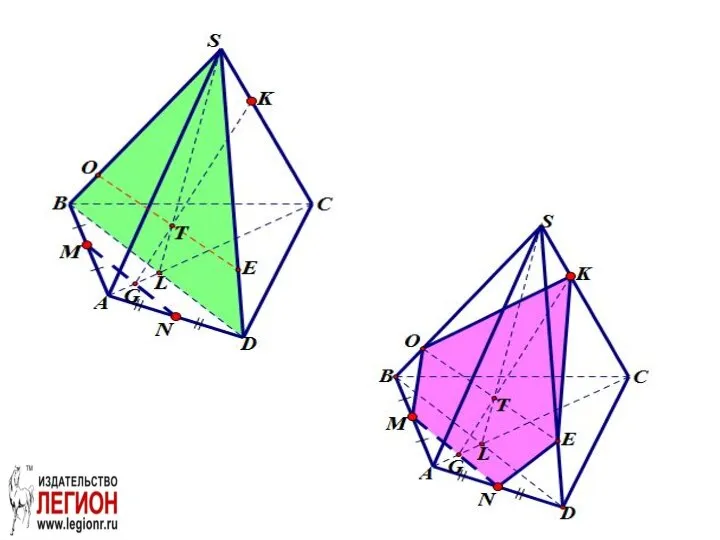
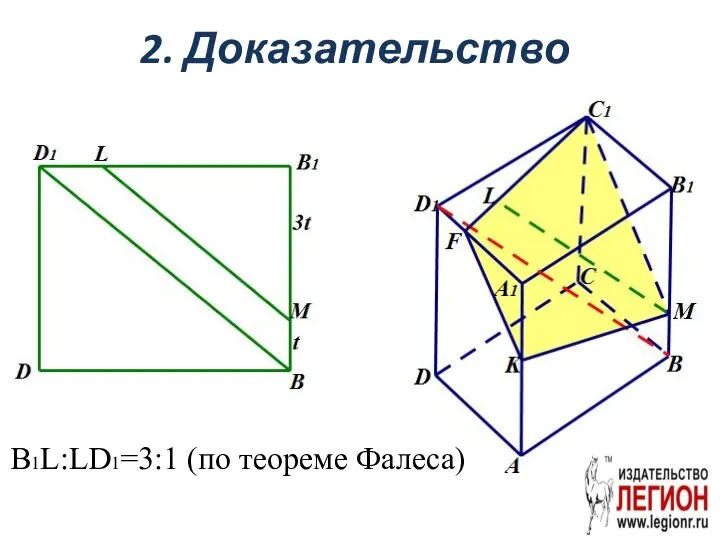
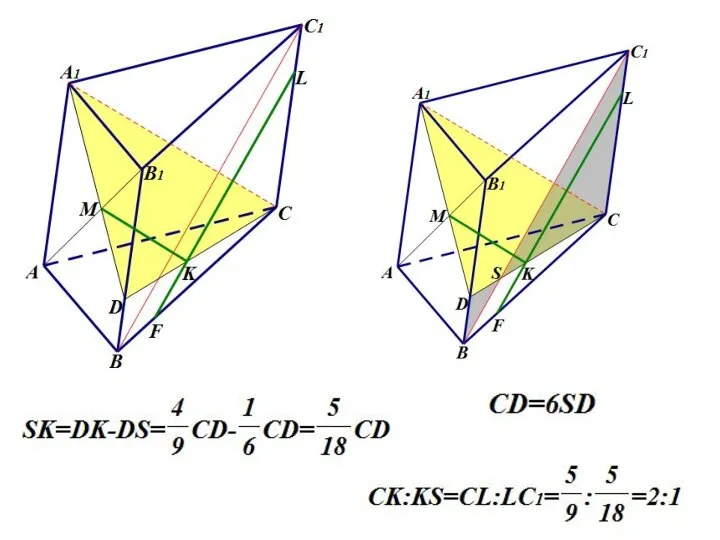
- 56. 2. Доказательство B1L:LD1=3:1 (по теореме Фалеса)
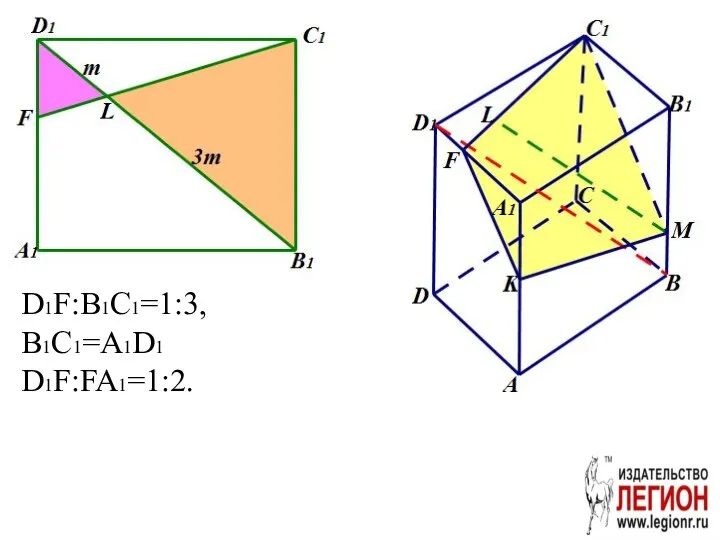
- 57. D1F:B1C1=1:3, B1C1=A1D1 D1F:FA1=1:2.
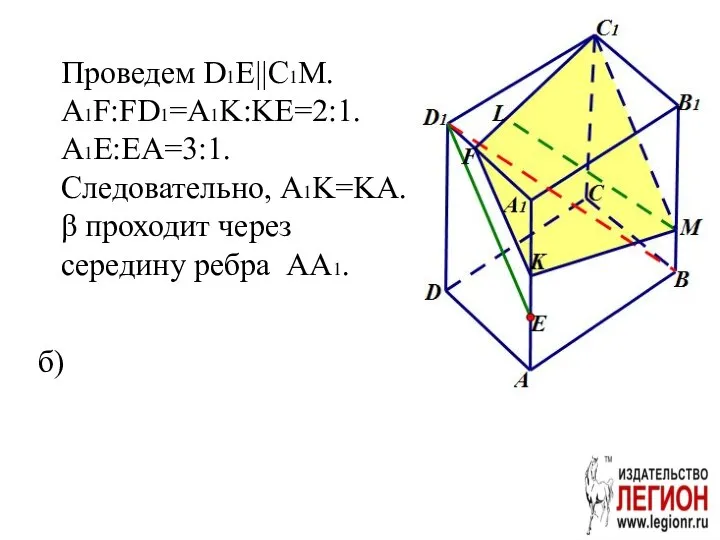
- 58. Проведем D1E||C1M. A1F:FD1=A1K:KE=2:1. A1E:EA=3:1. Следовательно, A1K=KA. β проходит через середину ребра AA1. б)
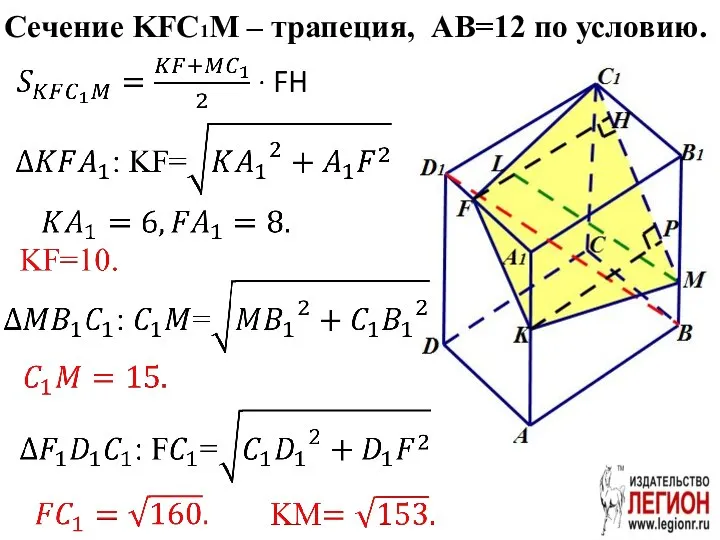
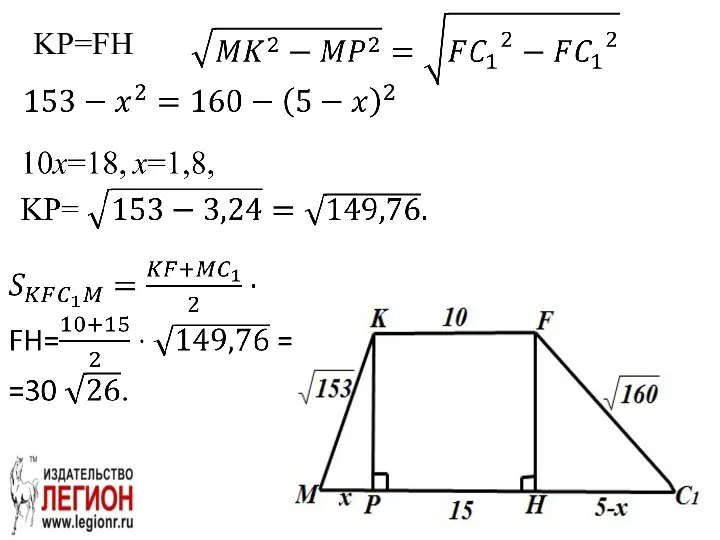
- 59. Сечение KFC1M – трапеция, AB=12 по условию.
- 60. KP=FH
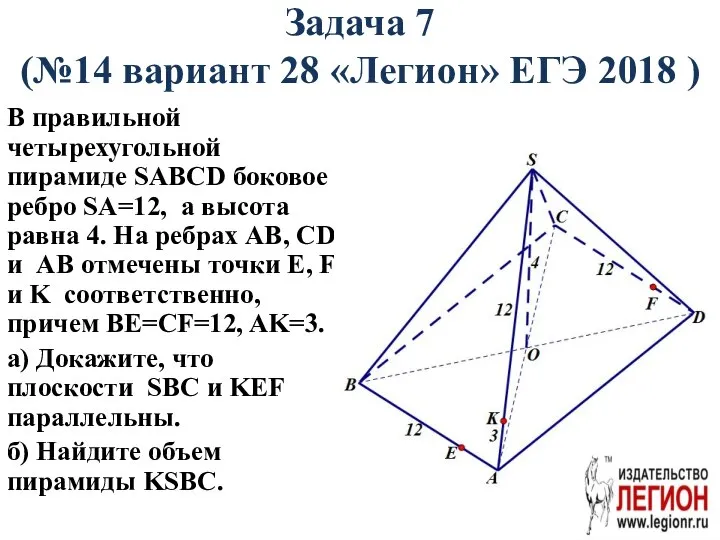
- 61. Задача 7 (№14 вариант 28 «Легион» ЕГЭ 2018 ) В правильной четырехугольной пирамиде SABCD боковое ребро
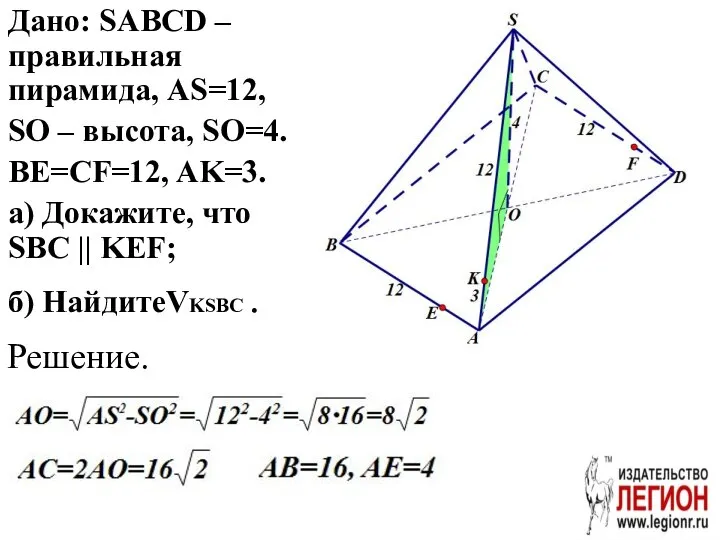
- 62. Дано: SABCD – правильная пирамида, AS=12, SO – высота, SO=4. BE=CF=12, AK=3. а) Докажите, что SBC
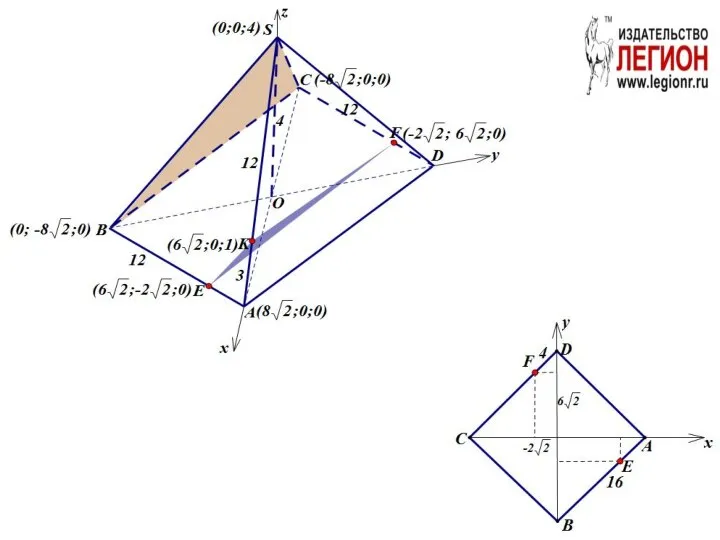
- 64. Решение. Способ 1 ⇔
- 65. Способ 2
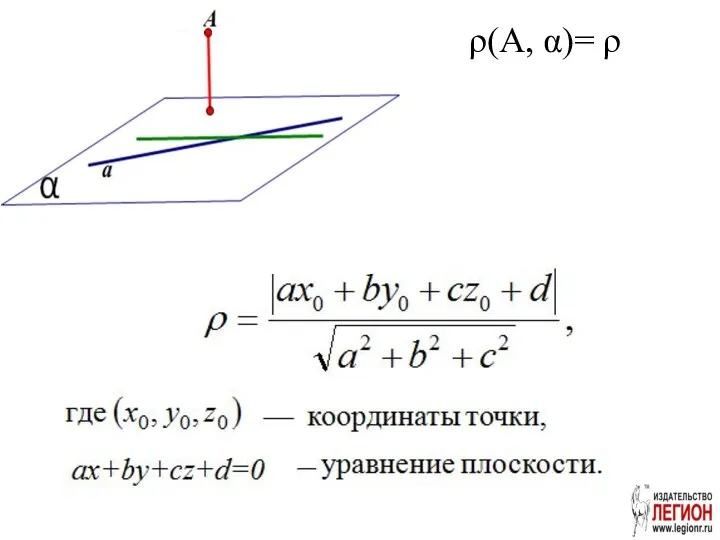
- 67. ρ(A, α)= ρ
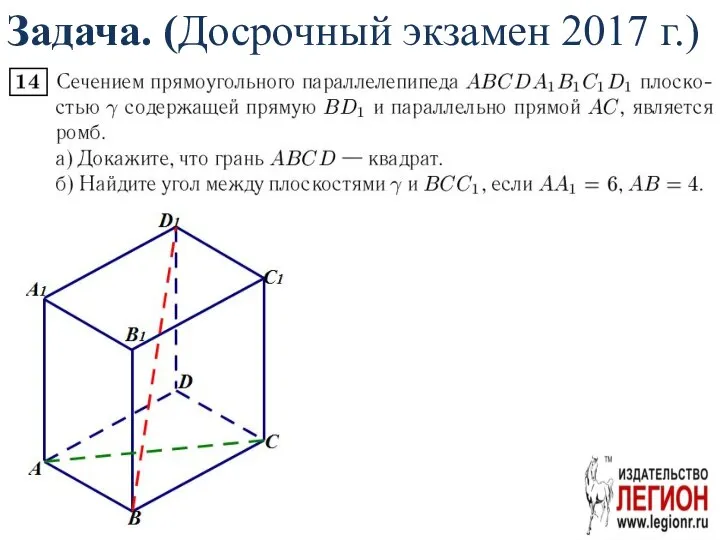
- 69. Задача. (Досрочный экзамен 2017 г.)
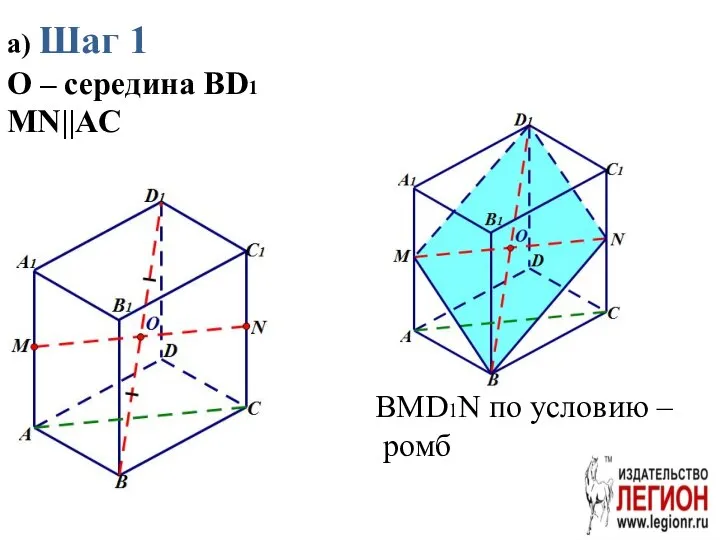
- 70. а) Шаг 1 O – середина BD1 MN||AC BMD1N по условию – ромб
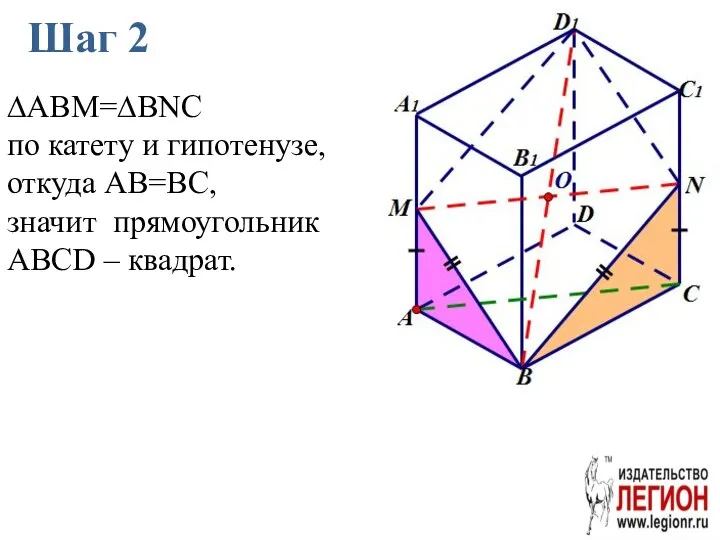
- 71. Шаг 2 ∆ABM=∆BNC по катету и гипотенузе, откуда AB=BC, значит прямоугольник ABCD – квадрат.
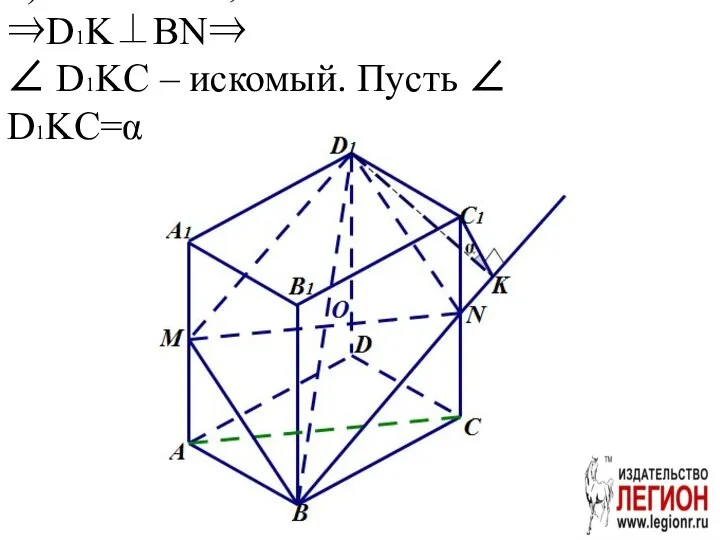
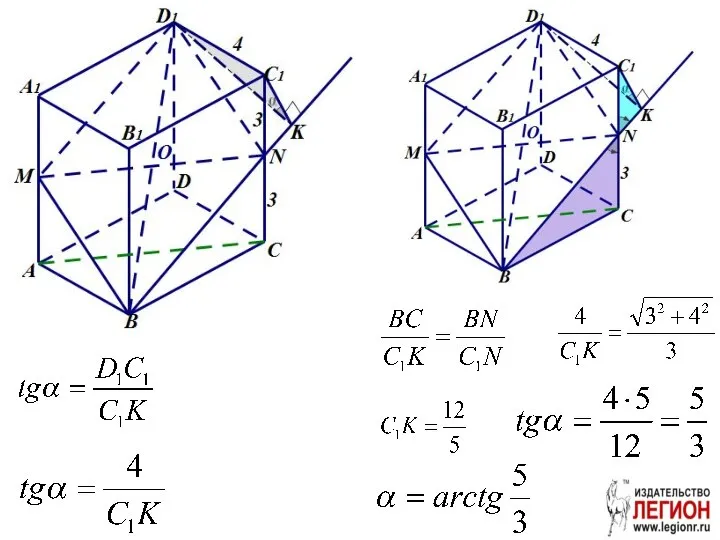
- 72. б) C1K ⊥ BN,D1C1⊥BCC1 ⇒D1K⊥BN⇒ ∠ D1KC – искомый. Пусть ∠ D1KC=α.
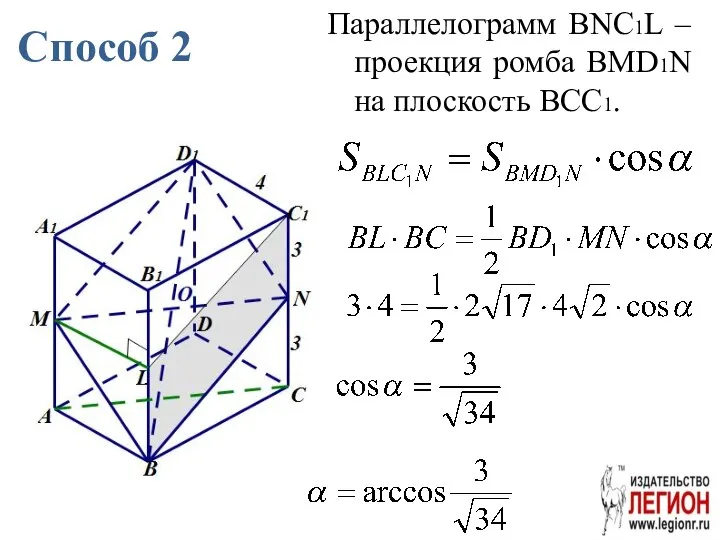
- 74. Способ 2 Параллелограмм BNC1L – проекция ромба BMD1N на плоскость BCC1.
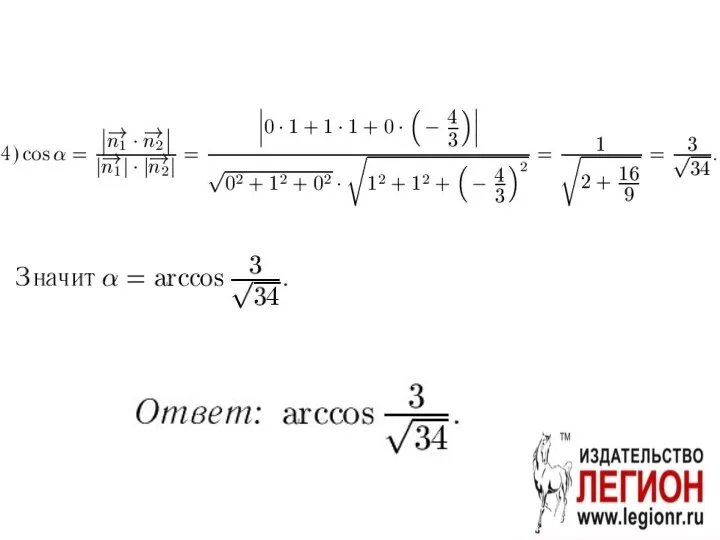
- 75. Способ 3
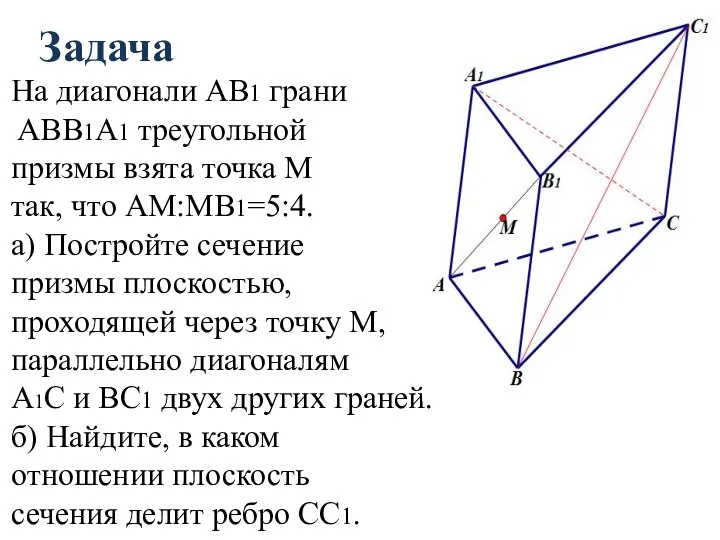
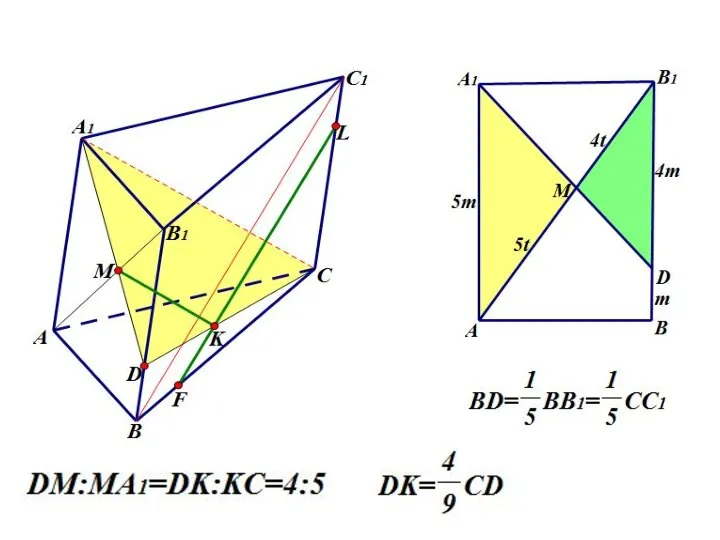
- 77. Задача На диагонали AB1 грани ABB1А1 треугольной призмы взята точка M так, что AM:MB1=5:4. а) Постройте
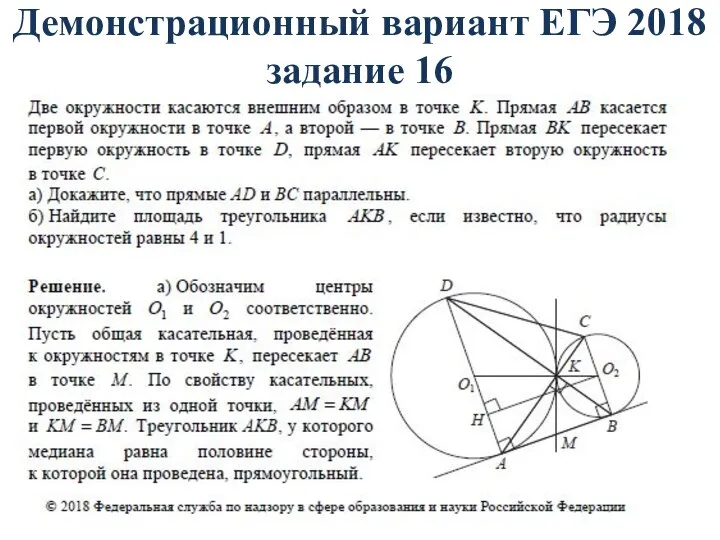
- 81. Демонстрационный вариант ЕГЭ 2018 задание 16
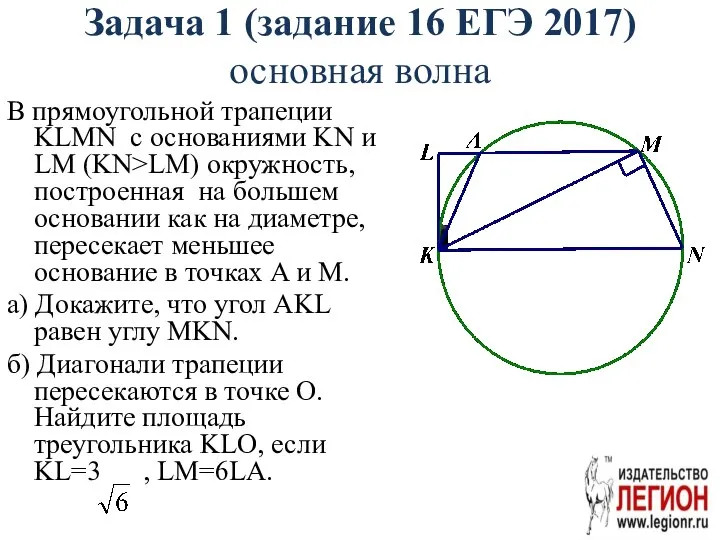
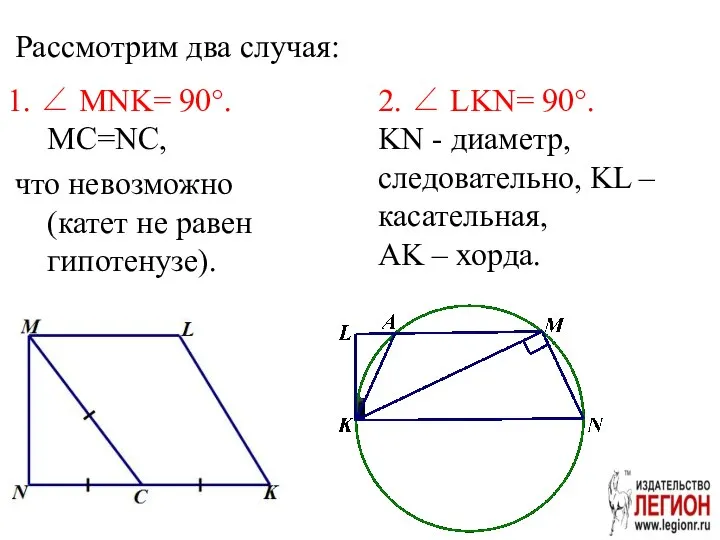
- 84. Задача 1 (задание 16 ЕГЭ 2017) основная волна В прямоугольной трапеции KLMN с основаниями KN и
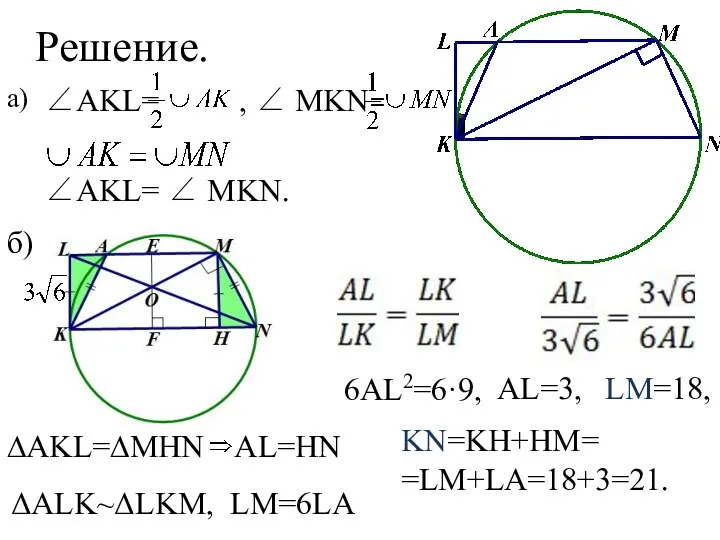
- 85. Рассмотрим два случая: 1. ∠ MNK= 90°. MC=NC, что невозможно (катет не равен гипотенузе). 2. ∠
- 86. Решение. ∠AKL= , ∠ MKN= ∠AKL= ∠ MKN. а) б) ∆AKL=∆MHN AL=HN ΔALK~ΔLKM, LM=6LA 6AL2=6·9, AL=3,
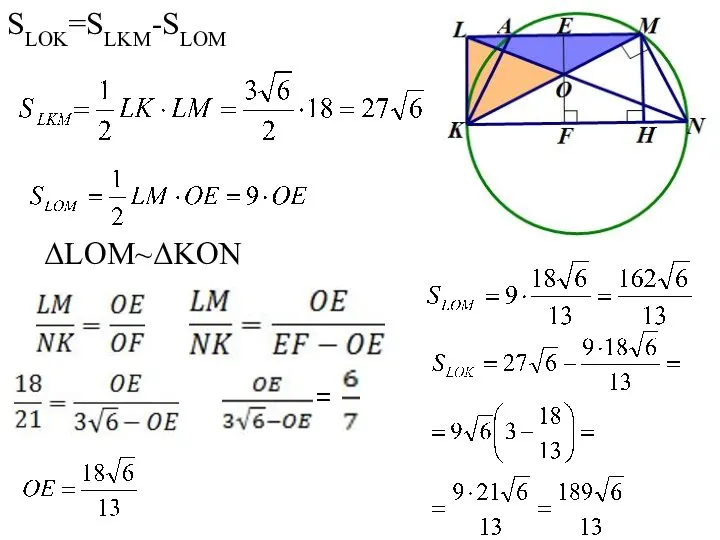
- 87. SLOK=SLKM-SLOM ΔLOM~ΔKON =
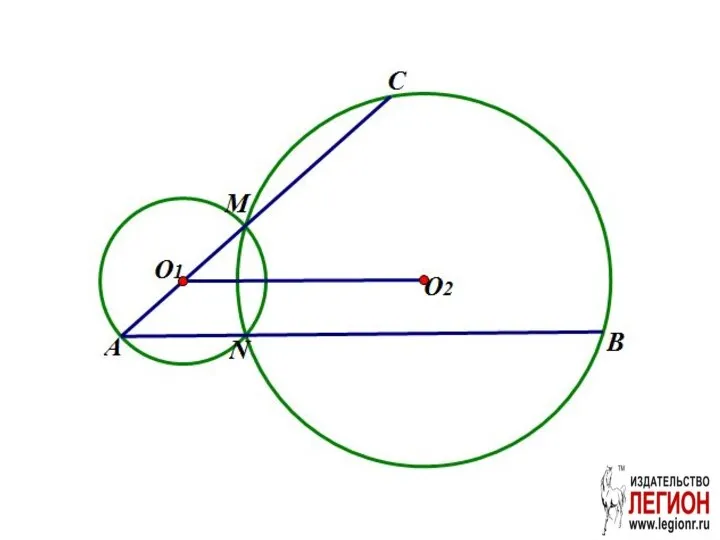
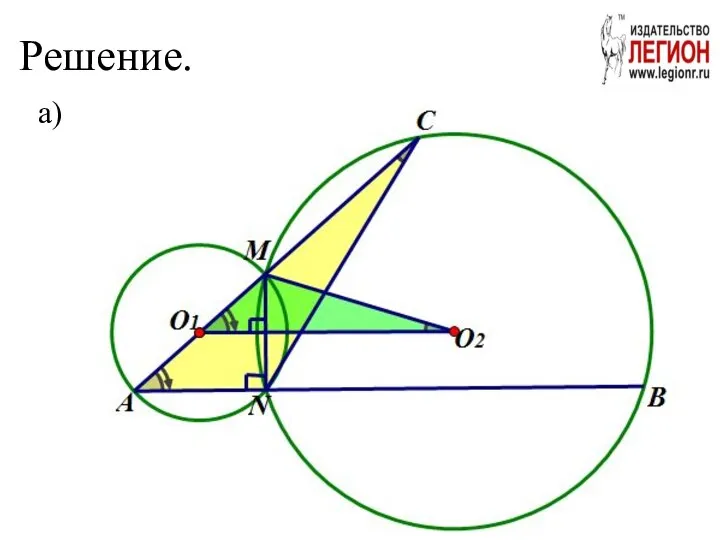
- 88. Задача (№16 вариант 15 «Легион» ЕГЭ 2018 ) Две окружности с центрами O1 и O2 пересекаются
- 90. Решение. а)
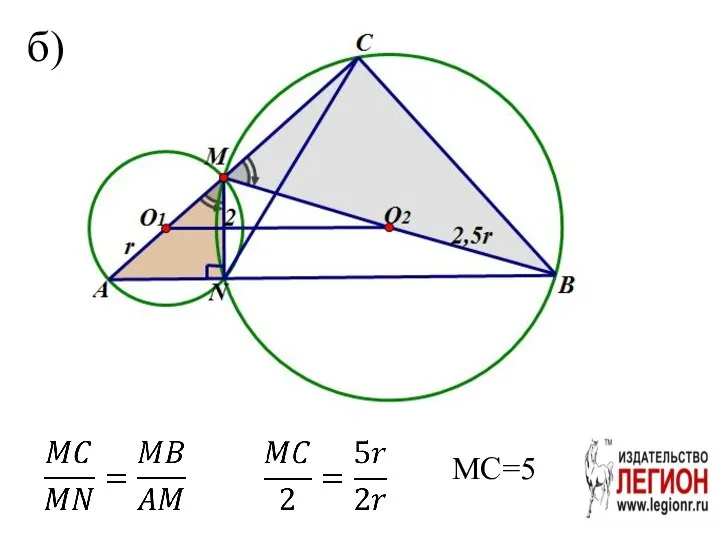
- 91. б) MC=5
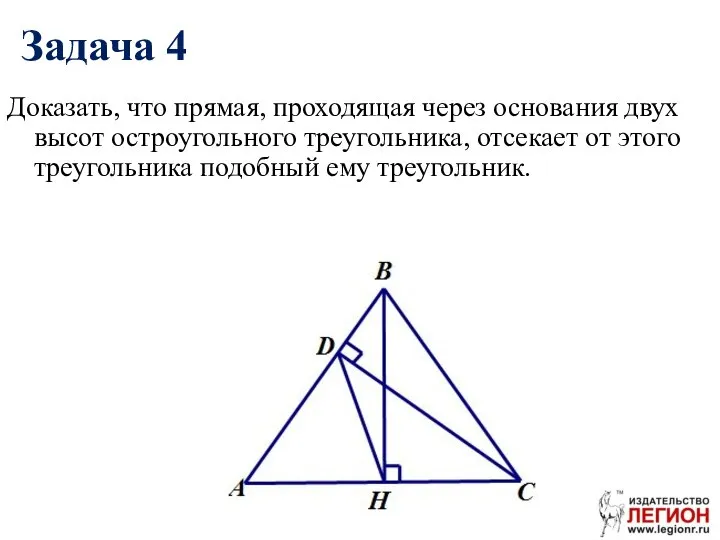
- 92. Доказать, что прямая, проходящая через основания двух высот остроугольного треугольника, отсекает от этого треугольника подобный ему
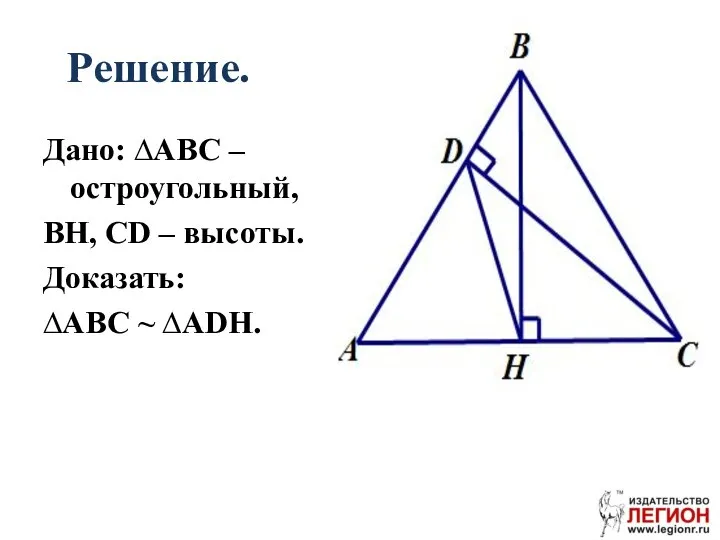
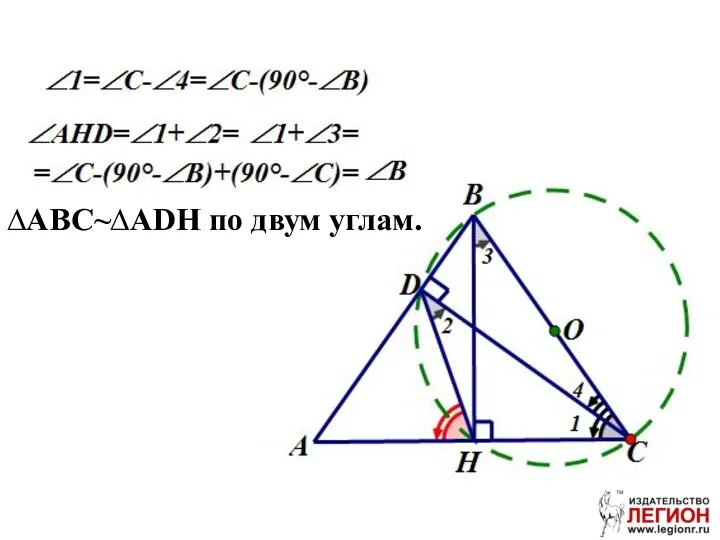
- 93. Решение. Дано: ∆ABC – остроугольный, BH, CD – высоты. Доказать: ∆ABC ~ ∆ADH.
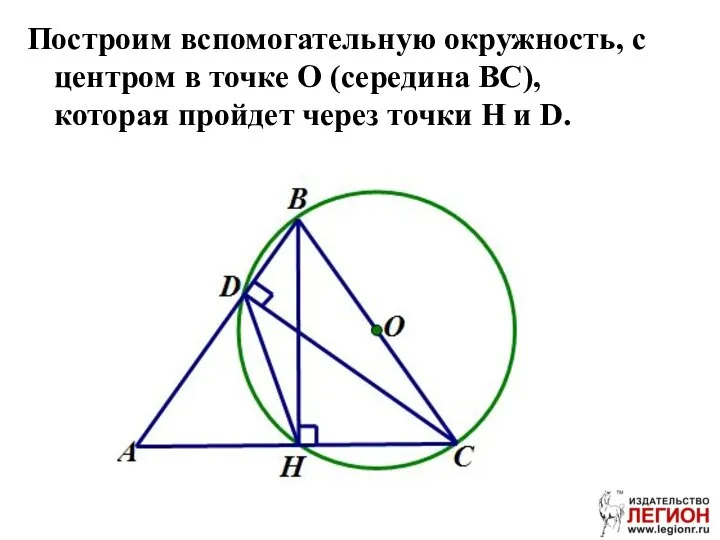
- 94. Построим вспомогательную окружность, с центром в точке О (середина ВС), которая пройдет через точки H и
- 95. ∆ABC~∆ADH по двум углам.
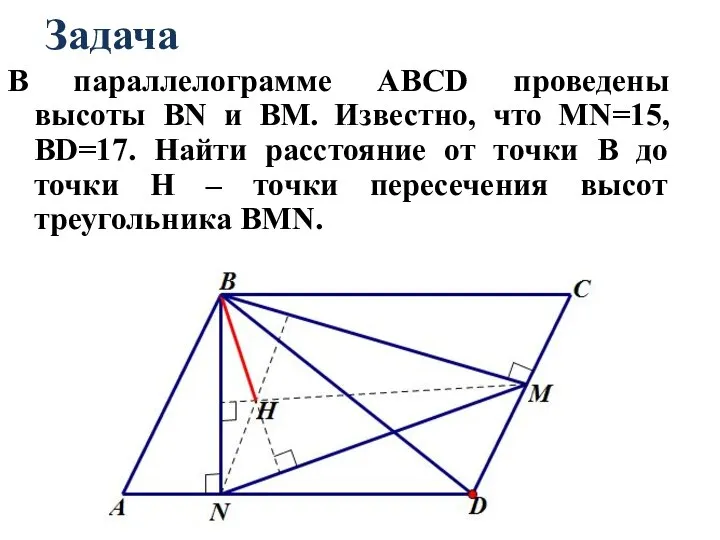
- 96. Задача В параллелограмме АВСD проведены высоты ВN и ВМ. Известно, что МN=15, ВD=17. Найти расстояние от
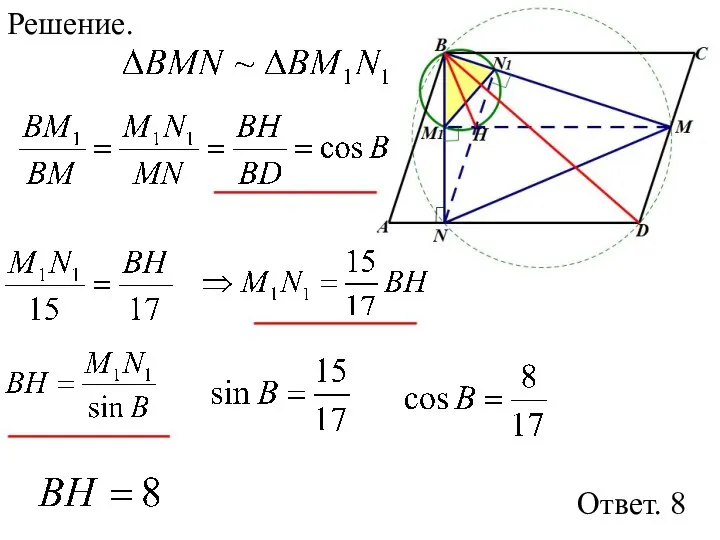
- 97. Решение. Ответ. 8
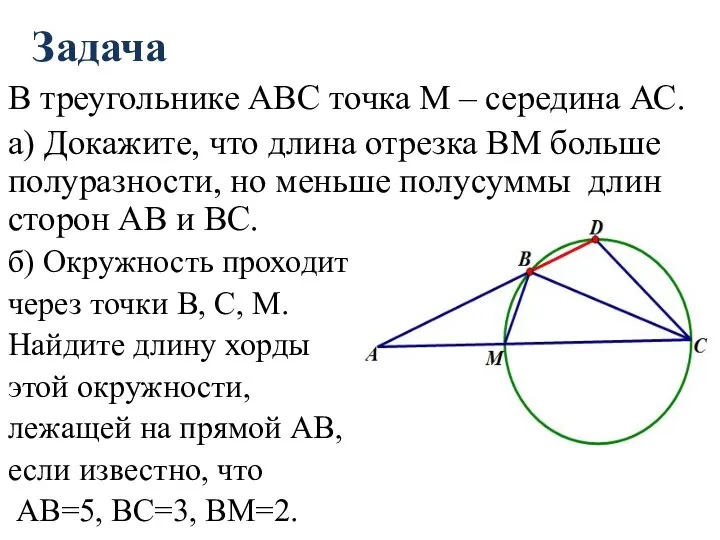
- 98. Задача В треугольнике АВС точка М – середина АС. а) Докажите, что длина отрезка ВМ больше
- 100. Скачать презентацию












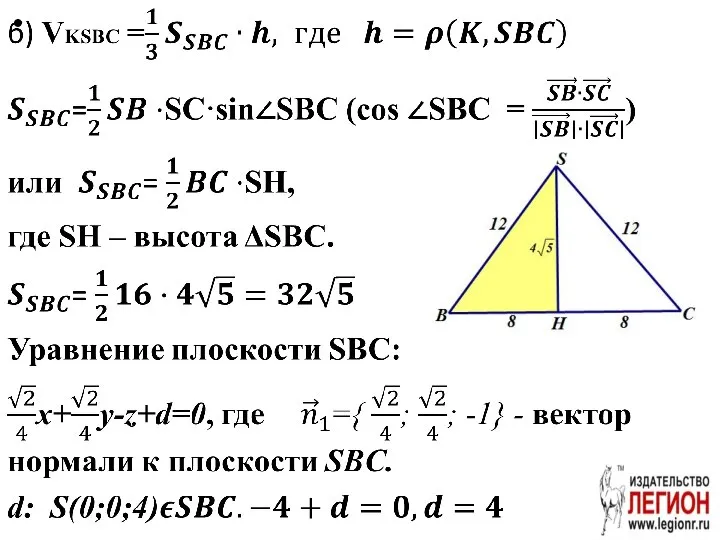
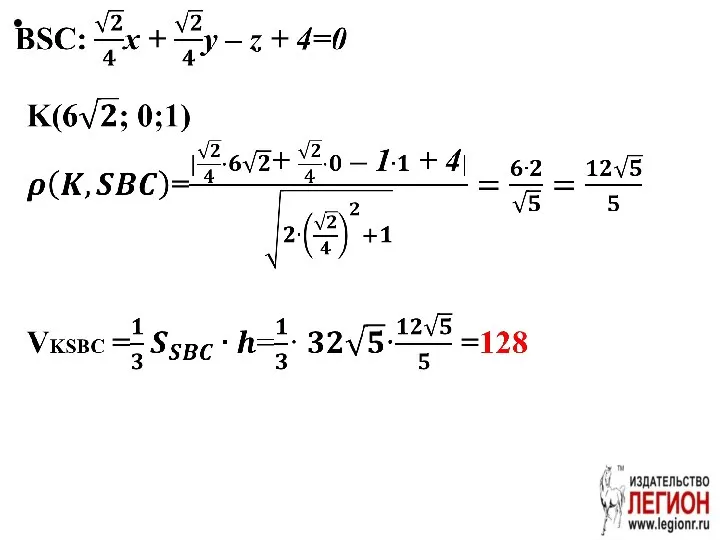




 Математикалық шамалар және олардың симметриясы
Математикалық шамалар және олардың симметриясы Презентация по математике "Средняя линия треугольника" - скачать
Презентация по математике "Средняя линия треугольника" - скачать  Скорость. Единицы скорости. Взаимосвязь между скоростью, временем и расстоянием
Скорость. Единицы скорости. Взаимосвязь между скоростью, временем и расстоянием Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани
Сложение и вычитание десятичных дробей. 18 февраля в истории Кубани Решение линейных уравнений. 7 класс
Решение линейных уравнений. 7 класс Занимательные задачи
Занимательные задачи Создатели теории множеств (во второй половине XIX века)
Создатели теории множеств (во второй половине XIX века) Осевая и центральная симметрия
Осевая и центральная симметрия Многочлены от одной переменной
Многочлены от одной переменной Презентация по математике "Приёмы деления" - скачать
Презентация по математике "Приёмы деления" - скачать  Объединение событий
Объединение событий  Сокращение дробей
Сокращение дробей Презентация по математике "ДРОБНЫЕ ВЫРАЖЕНИЯ (6 КЛАСС)" - скачать бесплатно
Презентация по математике "ДРОБНЫЕ ВЫРАЖЕНИЯ (6 КЛАСС)" - скачать бесплатно Приведите примеры элементарных исследований свойств при изучении первых функций
Приведите примеры элементарных исследований свойств при изучении первых функций Точки на прямой
Точки на прямой Решение линейных уравнений с параметром и модулем
Решение линейных уравнений с параметром и модулем Анаграмма. Великолепная семерка
Анаграмма. Великолепная семерка Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Аттестационная работа. Рабочая программа математического кружка «Юные математики». (6 класс)
Аттестационная работа. Рабочая программа математического кружка «Юные математики». (6 класс) Презентация по теме «Движение. Виды движения.»
Презентация по теме «Движение. Виды движения.»  Геометрические иллюзии, или всегда ли мы видим то, что видим
Геометрические иллюзии, или всегда ли мы видим то, что видим Формулы сокращенного умножения. Преобразование выражений
Формулы сокращенного умножения. Преобразование выражений Решение уравнений. 6 класс
Решение уравнений. 6 класс Показательные уравнения
Показательные уравнения Многоугольники
Многоугольники Решение треугольников
Решение треугольников Сечения
Сечения Эконометрика. Лекция 2
Эконометрика. Лекция 2