Многомерный регрессионный анализ. Использование для решения задачи однооткликового метода наименьших квадратов
Содержание
- 2. 4. Многомерный регрессионный анализ Общая (теоретическая) последовательность решения для получения коэффициентов и оценки точности для множественной
- 3. 4. Многомерный регрессионный анализ 2. Запишем целевую функцию Ф которую надо минимизировать в точке ai 3.
- 4. 4. Многомерный регрессионный анализ 4. Систему делим на 2, раскрываем сумму с группировкой и имеем совместную
- 5. 4. Многомерный регрессионный анализ Минимизация целевой функции в матричном виде по шагам: 1. Линейная модель в
- 6. 4. Многомерный регрессионный анализ Условие МНК – Ф = vTv = [v2] =min, Минимизация в матричном
- 7. 4. Многомерный регрессионный анализ Из вида уравнений поправок левая трансформация Гаусса та же совместная система нормальных
- 8. 4. Многомерный регрессионный анализ Практическая реализация по шагам: Составляется модель (например линейная многофакторная с 1-откликом) 2.
- 9. 4. Многомерный регрессионный анализ 3. Для системы нормальных уравнений строится матрица нормальных уравнений N и вектор
- 10. 4. Многомерный регрессионный анализ Графическая трактовка метода наименьших квадратов Модель в векторах - . Тогда имеем
- 11. 4. Многомерный регрессионный анализ Оценка точности: модель, коэффициенты модели ai, смоделированные величины и поправки v. Основа
- 12. 4. Многомерный регрессионный анализ - для оценки точности вектора коэффициентов регрессии а: Выражаем коэффициенты линейно через
- 13. 4. Многомерный регрессионный анализ Оценка через матрицу обратных весов Q (матрицу кофакторов) Оценка смоделированных значений .
- 14. 3. Многомерный регрессионный анализ Использование для решения задачи многооткликовой регрессии метода наименьших квадратов Основные виды: Матричный
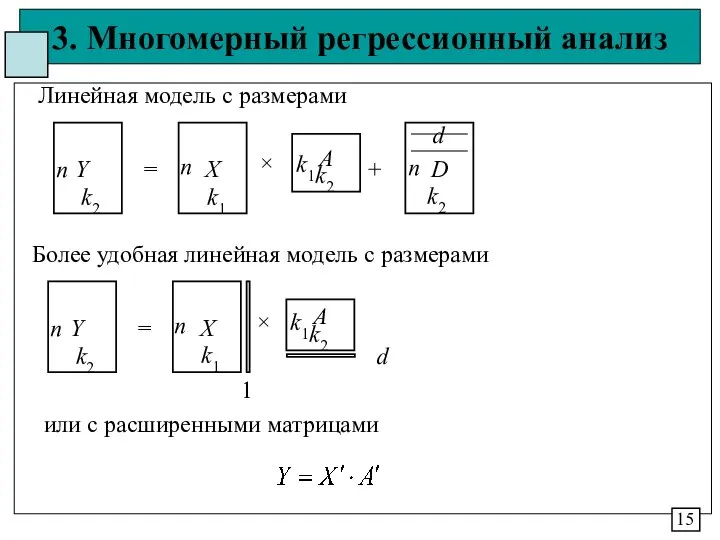
- 15. 3. Многомерный регрессионный анализ 15 k2 n Y = X k1 n × k1 k2 A
- 16. 3. Многомерный регрессионный анализ 16 Не дает естественную алгебраическую запись- транспонирование Реальная модель с матрицей поправок
- 17. 3. Многомерный регрессионный анализ Минимизация целевой функции Ф с совместная система нормальных уравнений через правую трансформацию
- 18. 3. Многомерный регрессионный анализ Оценка точности производится по обычной схеме: – погрешность модели п0 – число
- 19. 3. Многомерный регрессионный анализ – погрешности определения коэффициентов через ковариационную матрицу где матрица кофакторов оцененных параметров
- 21. Скачать презентацию

















 Лист Мёбиуса
Лист Мёбиуса Моделирование ситуаций. Виды моделей
Моделирование ситуаций. Виды моделей Отрезок. Лабораторно-практическая работа
Отрезок. Лабораторно-практическая работа Урок математики «Закрепление письменных приемов сложения и вычитания» Учитель: Циндяйкина С. А. 2 класс
Урок математики «Закрепление письменных приемов сложения и вычитания» Учитель: Циндяйкина С. А. 2 класс  Презентация по математике "Рациональные уравнения" - скачать бесплатно
Презентация по математике "Рациональные уравнения" - скачать бесплатно Меньше на некоторое число.
Меньше на некоторое число. Область определения выражения
Область определения выражения Вписанная и описанная окружность
Вписанная и описанная окружность Презентация на тему Наибольший общий делитель. Взаимно простые числа.
Презентация на тему Наибольший общий делитель. Взаимно простые числа. Метод математической индукции
Метод математической индукции Проверка статистических гипотез
Проверка статистических гипотез Разложение многочленов на множители с помощью комбинации различных приемов, решение уравнений. 7 класс
Разложение многочленов на множители с помощью комбинации различных приемов, решение уравнений. 7 класс Решение транспортной задачи. Составление опорного плана
Решение транспортной задачи. Составление опорного плана Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Статистические группировки
Статистические группировки Задачи С4. Как находить высоты и биссектрисы треугольника
Задачи С4. Как находить высоты и биссектрисы треугольника Логические задачи
Логические задачи Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Таблиця множення числа 3. Знаходження значень виразів на дії різних ступенів
Таблиця множення числа 3. Знаходження значень виразів на дії різних ступенів Решение неравенств
Решение неравенств Связь между автоматами Мили и Мура
Связь между автоматами Мили и Мура Кривые второго порядка
Кривые второго порядка Мінімізація скінченного автомата. (Тема 5)
Мінімізація скінченного автомата. (Тема 5) Проектирование разноритмичных и неритмичных потоков
Проектирование разноритмичных и неритмичных потоков МАТЕМАТИКА 1 КЛАСС
МАТЕМАТИКА 1 КЛАСС ЕГЭ 2016. Базовый уровень
ЕГЭ 2016. Базовый уровень Презентация по математике "Кабінет" - скачать
Презентация по математике "Кабінет" - скачать  Преобразования графика функции f(x)=x2
Преобразования графика функции f(x)=x2