Содержание
- 2. Основанием смешанной системы счисления называется множество из r≥2 целых чисел n1,n2,…,nr, не обязательно взаимно простых. Если
- 3. Пусть n1,n2,…,nr – попарно взаимно простые числа. Пусть nj и Ci – обратные к Ni по
- 4. Формулы определения цифр z1= x1mod n1, z2= C2(x2-z1) mod n2, z3= C3(x3-(N2z2+z1)) mod n3, … zr=
- 5. x1=z1, x2=(z1+z2n1)mod n2, x3=(z1+z2n1+z3n1n2)mod n3, … xr=(z1+z2n1+…+zrn1n2…nr-1)mod nr.
- 6. Сравнение двух целых чисел Пусть имеются два целых числа x и x', заданные своими модулярными компонентами,
- 7. Определение цифр в позиционной системе счисления Пусть целое х задано модулярными компонентами. Мы хотим вычислить его
- 9. Скачать презентацию



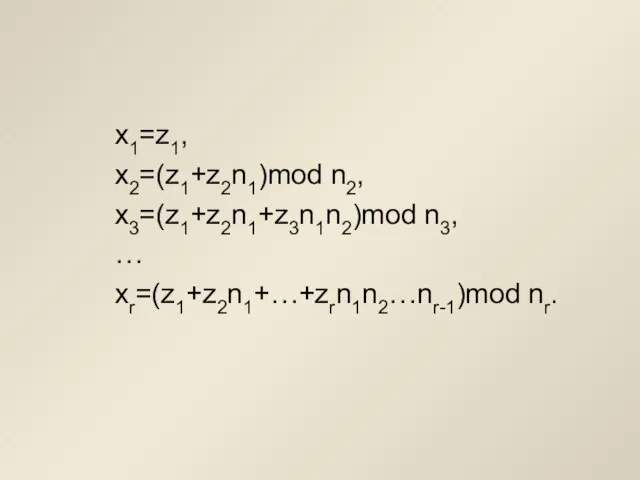


 Бесконечно малые величины
Бесконечно малые величины Применение подобия к доказательству теорем и решению задач. Урок 40
Применение подобия к доказательству теорем и решению задач. Урок 40 Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Методика изучения длины
Методика изучения длины Финансово-экономические расчеты: простой и сложный процент. 8 класс
Финансово-экономические расчеты: простой и сложный процент. 8 класс Мир геометрии
Мир геометрии В стране математики. Сценарий праздника
В стране математики. Сценарий праздника Гармония красоты. Особенности золотого сечения
Гармония красоты. Особенности золотого сечения Осевая и центральная симметрии
Осевая и центральная симметрии Процедуры и функции работы со строками
Процедуры и функции работы со строками Парная (простая) регрессия в эконометрических расчетах
Парная (простая) регрессия в эконометрических расчетах Элементы комбинаторики в школьном курсе математики
Элементы комбинаторики в школьном курсе математики Свойства числовых неравенств
Свойства числовых неравенств Жиындар
Жиындар Программирование графики
Программирование графики Звичайні дроби
Звичайні дроби Длина окружности
Длина окружности Путешествие в море неизвестных слагаемых и вычитаемых
Путешествие в море неизвестных слагаемых и вычитаемых Презентация по математике "Прогрессии" - скачать
Презентация по математике "Прогрессии" - скачать  Линейная парная регрессия
Линейная парная регрессия Элементарные функции. (Семинар 1)
Элементарные функции. (Семинар 1) Численные методы алгебры
Численные методы алгебры Показательная функция, её свойства и график
Показательная функция, её свойства и график Умножение и деление. Решаем задачи. (Тест 8. 3 класс)
Умножение и деление. Решаем задачи. (Тест 8. 3 класс) Решение задач в одно действие на сложение и вычитание
Решение задач в одно действие на сложение и вычитание  Эконометрика-1. Введение. Корреляционный анализ
Эконометрика-1. Введение. Корреляционный анализ Сложение и вычитание многозначных чисел
Сложение и вычитание многозначных чисел Презентация по математике "Геометрия в звездном небе. Свойство углов треугольника" - скачать бесплатно
Презентация по математике "Геометрия в звездном небе. Свойство углов треугольника" - скачать бесплатно