Содержание
- 2. Метод интегрирования по частям. Пусть дифференцируемые функции известно тогда проинтегрируем
- 3. то Если интеграл, стоящий справа, проще интеграла, стоящего слева, то применение формулы имеет смысл.
- 4. Пример 1. Вычислить интеграл
- 5. Некоторые типы интегралов, решаемые методом интегрирования по частям. где Р(х)- многочлен u u u u u
- 6. u=P(x) - многочлен Если Р(х) выше первой степени, то операцию интегрирования по частям следует применять несколько
- 7. Пример 2. Вычислить интеграл
- 8. Пример 3. Вычислить интеграл
- 10. Пример 4. Вычислить интеграл
- 11. Пусть тогда
- 12. Ответ:
- 14. Скачать презентацию









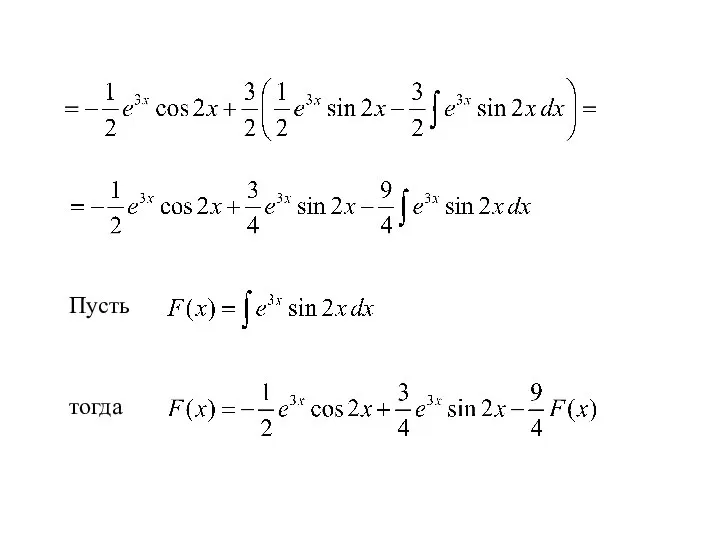
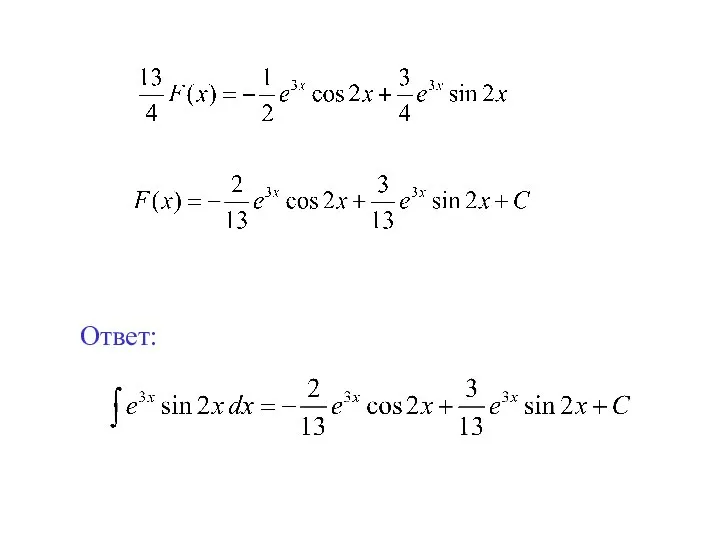
 Полуфинал. Экономический биатлон. День направления “Экономика и математика”
Полуфинал. Экономический биатлон. День направления “Экономика и математика” Математика в пределах 10
Математика в пределах 10 Вынесение множителя из-под знака корня. Внесение множителя под знак корня
Вынесение множителя из-под знака корня. Внесение множителя под знак корня Аттестационная работа. Проектная работа Культура устного счета в изучении математики в России
Аттестационная работа. Проектная работа Культура устного счета в изучении математики в России Решение задач
Решение задач Презентация по математике "Математика – гимнастика ума" - скачать бесплатно
Презентация по математике "Математика – гимнастика ума" - скачать бесплатно Смежные углы
Смежные углы Комбинаторика. 5 класс
Комбинаторика. 5 класс ЕГЭ профильная математика. Задание № 4
ЕГЭ профильная математика. Задание № 4 Обобщение темы «Сечение». 10 класс
Обобщение темы «Сечение». 10 класс Пересечение поверхности плоскостью
Пересечение поверхности плоскостью Задачи на построение
Задачи на построение Способы решения квадратного уравнения
Способы решения квадратного уравнения Построение сечений параллелепипеда
Построение сечений параллелепипеда Таблица умножения с числом 9
Таблица умножения с числом 9 Презентация по математике Алгебраические дроби
Презентация по математике Алгебраические дроби  История возникновения дробей
История возникновения дробей Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Виды симметрии в архитектуре
Виды симметрии в архитектуре Аттестационная работа. Путешествие с математикой по родному городу
Аттестационная работа. Путешествие с математикой по родному городу Комбинаторные задачи на перестановки, размещения
Комбинаторные задачи на перестановки, размещения Определение числовой функции
Определение числовой функции Пишите грамотно решение неполных квадратных уравнений
Пишите грамотно решение неполных квадратных уравнений Математичні методи в біології
Математичні методи в біології Вектор на плоскости
Вектор на плоскости Точность коэффициентов множественной регрессии
Точность коэффициентов множественной регрессии Весёлая математика. Число и цифра 3
Весёлая математика. Число и цифра 3