Содержание
- 2. 1. Несобственные интегралы с бесконечными пределами интегрирования (1 рода) Пусть функция y=f(x) определена и интегрируема на
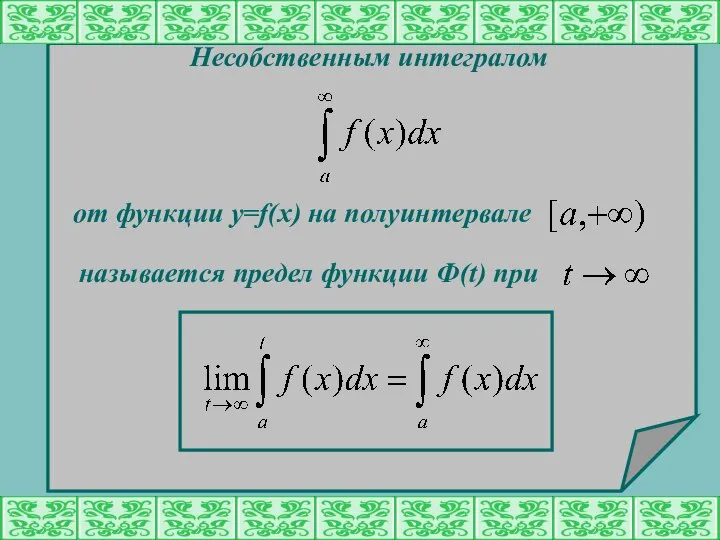
- 3. Несобственным интегралом от функции y=f(x) на полуинтервале называется предел функции Ф(t) при
- 4. Если такой предел существует и конечен, то несобственный интеграл называется сходящимся к данному пределу. Если конечного
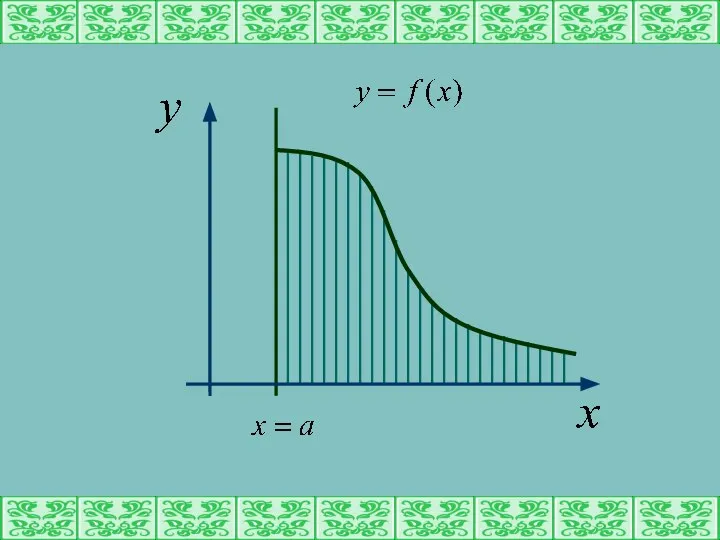
- 5. Геометрический смысл несобственного интеграла основан на геометрической интерпретации определенного интеграла на отрезке [a,t]. Это площадь бесконечной
- 7. Пример. Вычислить интеграл
- 8. Решение.
- 9. Аналогично можно определить несобственный интеграл на промежутке Рассмотрим несобственный интеграл на интервале Пусть для некоторого числа
- 10. - сходятся. Тогда положим и интеграл тоже сходится. Если хотя бы один из интегралов в левой
- 11. Пример. Вычислить интеграл
- 12. Решение. Исследуем на сходимость интегралы - сходится. - расходится. - расходится.
- 13. В рассмотренных примерах сначала с помощью первообразной вычислялся интеграл по конечному промежутку, а затем осуществлялся переход
- 14. Отсюда следует, что несобственный интеграл существует только в том случае, если существует конечный предел И тогда
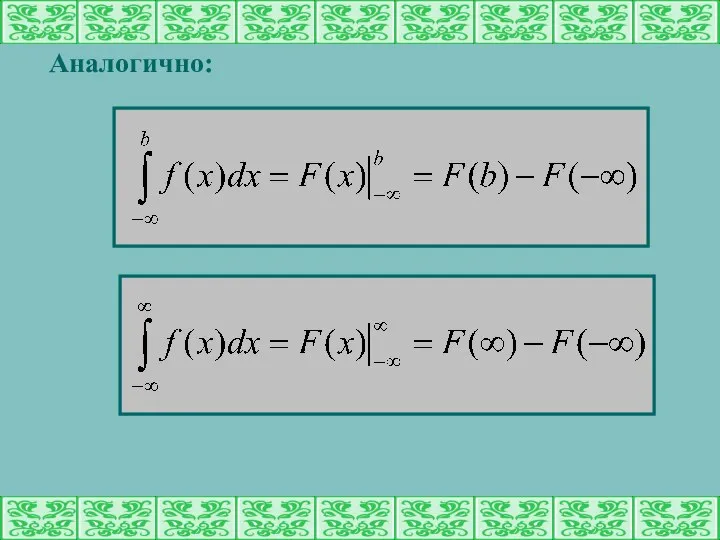
- 15. Аналогично:
- 16. Пример. Вычислить интеграл
- 17. Решение.
- 18. 2. Несобственные интегралы от неограниченных функций (2 рода) Пусть функция y=f(x) непрерывна, но неограничена на полуинтервале
- 19. Несобственным интегралом от функции y=f(x) на полуинтервале называется предел где
- 20. Если такой предел существует и конечен, то несобственный интеграл называется сходящимся. Если конечного предела не существует,
- 21. Аналогично можно ввести понятие несобственного интеграла от функции y=f(x) непрерывной но неограниченой на полуинтервале (a,b]:
- 22. Пример. Вычислить интеграл
- 23. Решение. Особая точка х=0.
- 24. ЗАМЕЧАНИЕ 1. Если функция y=f(x) неограничена при х=С, где то интеграл тоже называется несобственным:
- 25. ЗАМЕЧАНИЕ 2. Если a и b – особые точки, т.е. функция y=f(x) неограничена и интегрируема на
- 26. Пример. Вычислить интеграл
- 27. Решение. Особые точки: х=-1, х=1.
- 28. Пусть функция y=f(x) интегрируема на всем промежутке [a,b], причем b – особая точка. Если существует первообразная
- 29. Пример. Вычислить интеграл
- 31. Скачать презентацию




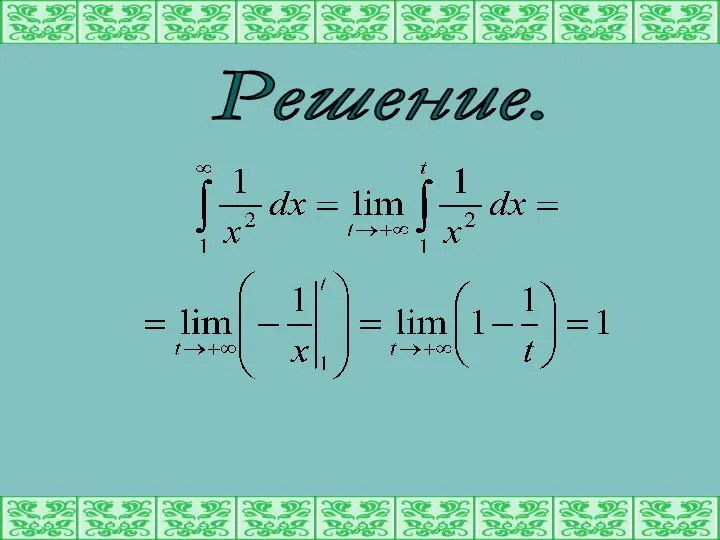











![Аналогично можно ввести понятие несобственного интеграла от функции y=f(x) непрерывной но неограниченой на полуинтервале (a,b]:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463576/slide-20.jpg)






![Пусть функция y=f(x) интегрируема на всем промежутке [a,b], причем b –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463576/slide-27.jpg)

 Табличные информационные модели
Табличные информационные модели Тригонометрические уравнения
Тригонометрические уравнения Понятие обратной функции
Понятие обратной функции Письменное умножение двух чисел, оканчивающихся нулями
Письменное умножение двух чисел, оканчивающихся нулями Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 Специальные распределения. χ2 -распределение
Специальные распределения. χ2 -распределение Корреляционный анализ. Парная корреляция
Корреляционный анализ. Парная корреляция Таблица умножения. Тренажер
Таблица умножения. Тренажер Параллельные прямые. Игра "Русское лото"
Параллельные прямые. Игра "Русское лото" Сравнение дробей
Сравнение дробей Парабола и ее применение
Парабола и ее применение Смешанные числа
Смешанные числа Координатная прямая
Координатная прямая Сумма углов треугольника
Сумма углов треугольника Таблица умножения и деления на 2
Таблица умножения и деления на 2 Математическая викторина для 5-6 классов
Математическая викторина для 5-6 классов Методы обработки данных и способы их представления в научном исследовании
Методы обработки данных и способы их представления в научном исследовании Умножение чисел с разными знаками
Умножение чисел с разными знаками Объединение множеств
Объединение множеств Число и цифра 5. Состав числа 5. Сложение и вычитание в пределах 5. Пятиугольник
Число и цифра 5. Состав числа 5. Сложение и вычитание в пределах 5. Пятиугольник История чисел
История чисел Решение задач по теме «Правильный многоугольник»
Решение задач по теме «Правильный многоугольник» Треугольники. Подготовка к ОГЭ. Задание 16
Треугольники. Подготовка к ОГЭ. Задание 16 Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Построение эскизов кривых в декартовых координатах. (Семинар 3)
Построение эскизов кривых в декартовых координатах. (Семинар 3) Решение игр в смешанных стратегиях
Решение игр в смешанных стратегиях Двугранный угол (ЕГЭ)
Двугранный угол (ЕГЭ)