Содержание
- 2. Построить многочлен (1) принимающий в заданных узлах заданные значения: (2) Получается система линейных уравнений относительно неизвестных
- 3. 1. Интерполяционный многочлен Лагранжа строится в виде: , где 2. Интерполяционный многочлен Ньютона имеет вид: Коэффициенты
- 4. где , Если достаточно гладкая, то погрешность стремится к нулю с увеличением n: О погрешностях интерполяционных
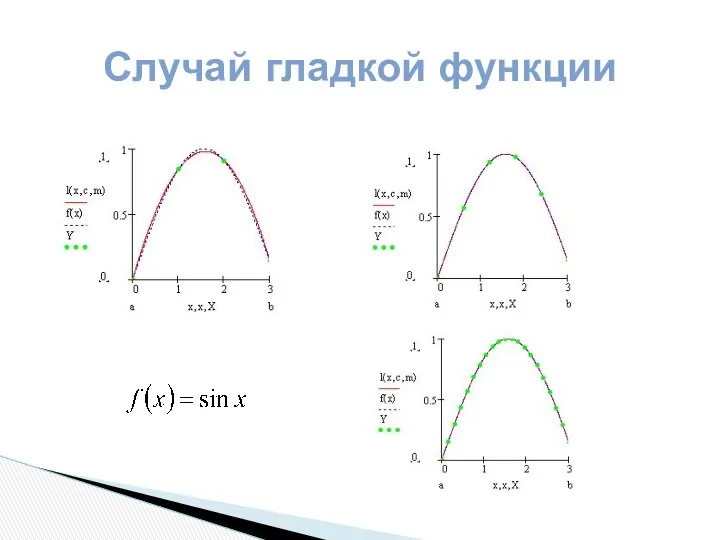
- 5. Случай гладкой функции
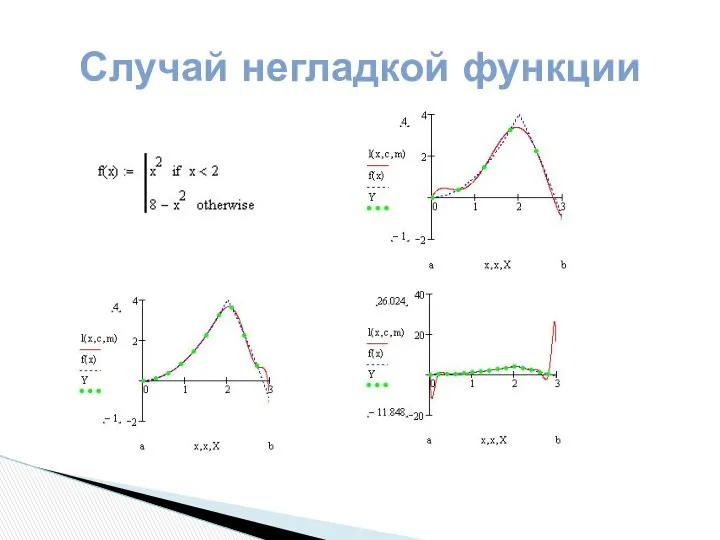
- 6. Случай негладкой функции
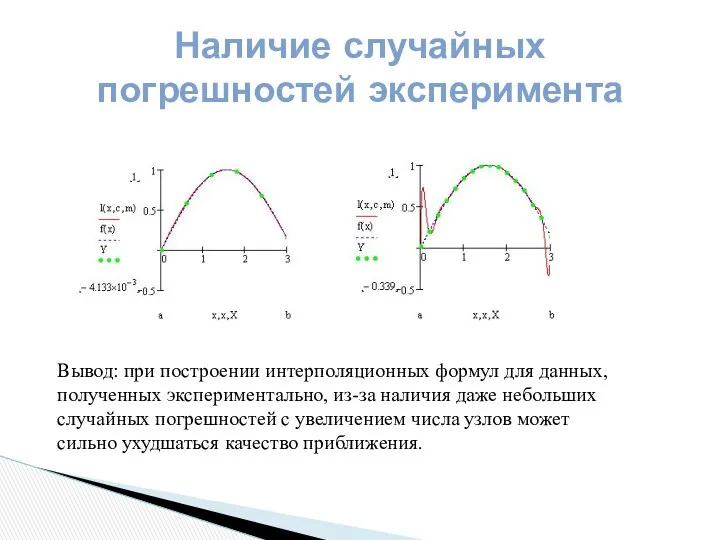
- 7. Наличие случайных погрешностей эксперимента Вывод: при построении интерполяционных формул для данных, полученных экспериментально, из-за наличия даже
- 8. На каждом промежутке строится многочлен третьей степени коэффициенты которого находятся из условий интерполяции и условий непрерывности
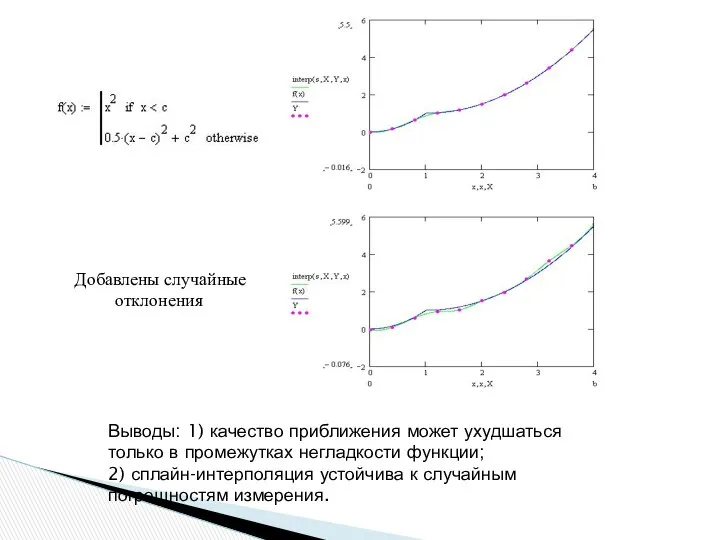
- 9. Добавлены случайные отклонения Выводы: 1) качество приближения может ухудшаться только в промежутках негладкости функции; 2) сплайн-интерполяция
- 10. Метод наименьших квадратов Задача: требуется приблизить функцию , заданную таблицей своих значений в точках в некотором
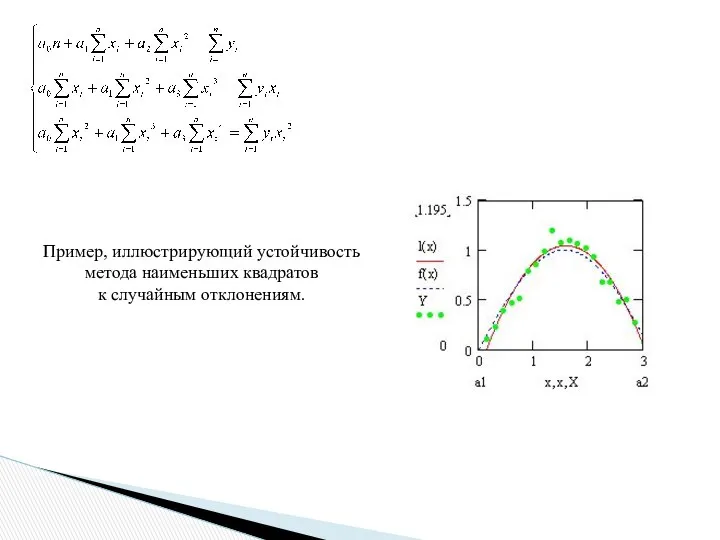
- 11. Пример, иллюстрирующий устойчивость метода наименьших квадратов к случайным отклонениям.
- 13. Скачать презентацию





 Нахождение дроби от числа и числа по его дроби
Нахождение дроби от числа и числа по его дроби Умножение вектора на число
Умножение вектора на число Перпендикуляр к прямой
Перпендикуляр к прямой Степенная функция. 10 класс
Степенная функция. 10 класс Чотирикутники
Чотирикутники Теория оптимизации
Теория оптимизации Алгебра высказываний при решении логических задач. Дизъюнктивные нормальные формы Лекция 3
Алгебра высказываний при решении логических задач. Дизъюнктивные нормальные формы Лекция 3 Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве
Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве Юбилейный ЕГЭ по математике «Вперед! Только вперед!»
Юбилейный ЕГЭ по математике «Вперед! Только вперед!» «Преданья старины далёкой» (Решение старинных задач) Южакова Елизавета 8 класс МОУ Новолялинская СОШ №4
«Преданья старины далёкой» (Решение старинных задач) Южакова Елизавета 8 класс МОУ Новолялинская СОШ №4 Қалдықпен бөлу
Қалдықпен бөлу Устная и письменная нумерация чисел в пределах 1000
Устная и письменная нумерация чисел в пределах 1000 Математическая викторина
Математическая викторина Сбор и группировка статистических данных
Сбор и группировка статистических данных МАТЕМАТИЧЕСКОЕ СТИХОТВОРЕНИЕ Сочинила: ученица 5 а класса ТЕТЮШЕВА АЛЕКСАНДРА МОУ СОШ с. Верхний Ломов Нижнеломовского района
МАТЕМАТИЧЕСКОЕ СТИХОТВОРЕНИЕ Сочинила: ученица 5 а класса ТЕТЮШЕВА АЛЕКСАНДРА МОУ СОШ с. Верхний Ломов Нижнеломовского района  ДЗ Математика 28.01.2021
ДЗ Математика 28.01.2021 Таблица умножения и деления на 5
Таблица умножения и деления на 5 Презентация по математике "Сложение и вычитание чисел." - скачать бесплатно_
Презентация по математике "Сложение и вычитание чисел." - скачать бесплатно_ Б Р Е Й Н – Р И Н Г
Б Р Е Й Н – Р И Н Г Умножение и деление дробных чисел 6 класс МАОУ СОШ №10 г.Краснокамска Минина Т.А.
Умножение и деление дробных чисел 6 класс МАОУ СОШ №10 г.Краснокамска Минина Т.А.  Пирамида – это многогранник, составленный из n-угольника
Пирамида – это многогранник, составленный из n-угольника Равновеликие многоугольники
Равновеликие многоугольники Своя игра. Действия с десятичными дробями
Своя игра. Действия с десятичными дробями Застосування похідної в різних областях науки
Застосування похідної в різних областях науки Квадрат суммы и разности
Квадрат суммы и разности Угол поворота. Радианная мера угла
Угол поворота. Радианная мера угла Интересные факты из математики
Интересные факты из математики Координатная плоскость
Координатная плоскость