Содержание
- 2. Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называется , если этот предел существует и не
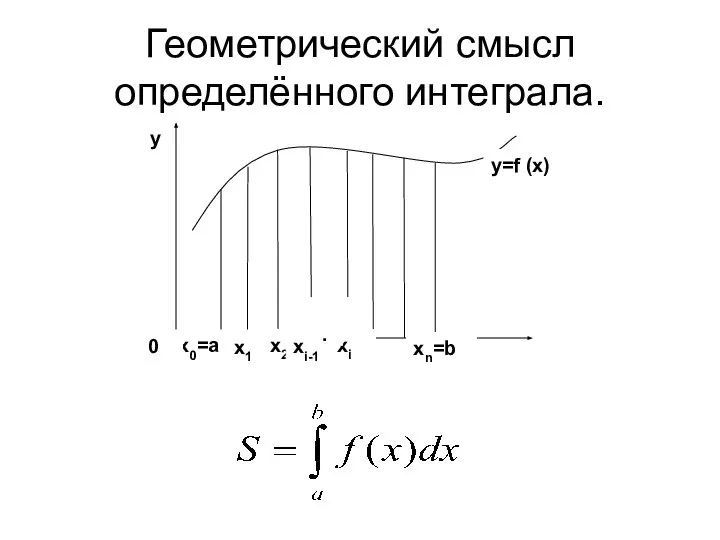
- 3. Геометрический смысл определённого интеграла.
- 4. Свойства определённого интеграла. 1. 2. 3. , k-любое число 4. 5.Аддитивность определённого интеграла. Для любых чисел
- 5. Формула Ньютона-Лейбница. Если F(x) есть какая-либо первообразная от непрерывной на [ , ] функции f(x), то
- 6. Пример.
- 7. Замена переменной в определённом интеграле.
- 8. Интегрирование по частям в определённом интеграле.
- 9. Пример.
- 10. Геометрические приложения определенного интеграла.
- 14. Площадь криволинейной трапеции, ограниченной кривой, заданной параметрически.
- 15. x(t), y(t), x’(t), y’(t) – непрерывны на , где
- 16. Пример. Найти площадь фигуры, ограниченной осью OX и одной аркой циклоиды:x= (t-sin t), y= (1-cos t).
- 17. Вычисление длины дуги кривой.
- 18. Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ].
- 19. Пусть кривая задана в параметрической форме x=x(t), y=y(t), t , причём x(t), y(t), x’(t) 0, y’(t)
- 20. Несобственный интеграл. Если существует конечный (b> ), то этот предел называется несобственным интегралом функции f(x) на
- 22. Пример.
- 23. Функции нескольких переменных.
- 24. Определение Функцией двух переменных называется правило, по которому каждой упорядоченной паре чисел (x;y), принадлежащей множеству M,
- 25. Частные производные.
- 26. Частные производные по x. Предел , если он существует, называется частной производной (I порядка) функции z=f(x,y)
- 27. Частные производные по y. называется частной производной (I порядка) функции z=f(x,y) по y в точке и
- 28. Частные производные высших порядков.
- 29. Пример. . Вычислить частные производные II порядка функции. , , , , , .
- 30. Полный дифференциал.
- 31. Скалярное поле. Часть пространства или всё пространство, в каждой точке p(x,y,z) которого задана скалярная функция U=F(x,
- 32. Производная по направлению.
- 33. Градиент
- 34. Экстремумы функции двух переменных.
- 35. Необходимое условие существования экстремума. Пусть функция z=f(x, y) в точке имеет экстремум и пусть существует и
- 36. Достаточное условие существования экстремума. Пусть для функции z=f(x, y) в критической точке существуют производные , ,
- 37. Пример исследовать на экстремум функцию Решение. ; . Решая систему получим четыре стационарные точки
- 39. Скачать презентацию
![Определенный интеграл. Определенным интегралом функции y=f(x) на [a,b] называется , если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1257348/slide-1.jpg)





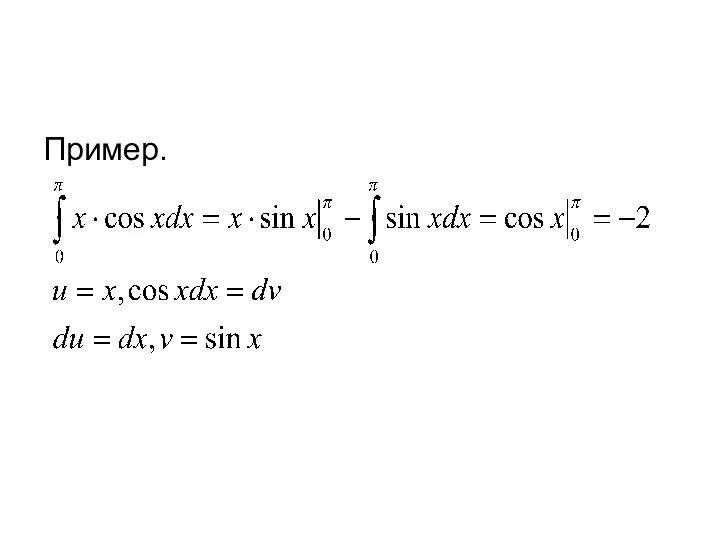








![Пусть кривая задана уравнением y=f(x), где f(x) и f’(x) непрерывны на [ , ].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1257348/slide-17.jpg)


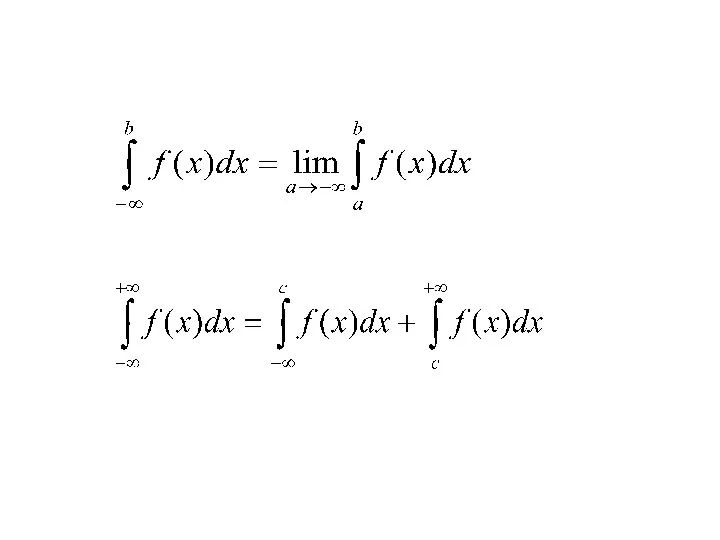
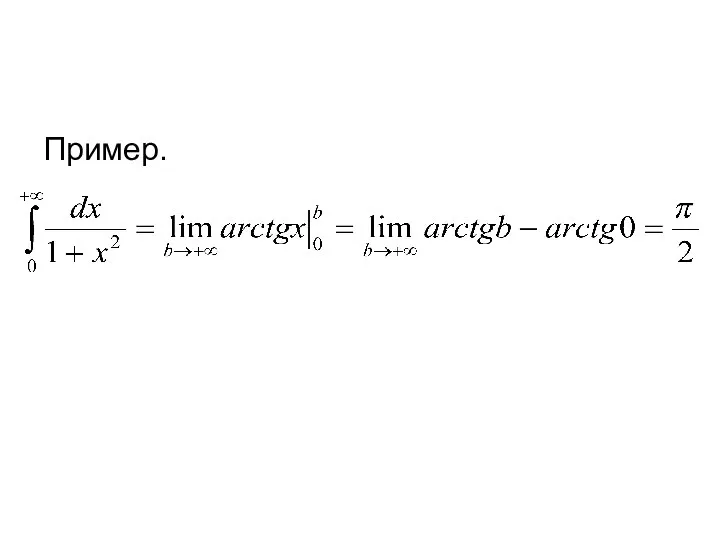















 Дроби
Дроби Решение уравнений. Урок-обобщение
Решение уравнений. Урок-обобщение Линейные неравенства с одним неизвестным. 9 класс
Линейные неравенства с одним неизвестным. 9 класс Пифагоровы тройки чисел
Пифагоровы тройки чисел Основы логики. Таблица истинности. Равносильные логические выражения
Основы логики. Таблица истинности. Равносильные логические выражения Лінійна алгебра. Матриці
Лінійна алгебра. Матриці Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Кут між прямими. Перпендикулярність прямих, прямої і площини. Перпендикуляр і похила до площини
Кут між прямими. Перпендикулярність прямих, прямої і площини. Перпендикуляр і похила до площини Нахождение свойств производной по графику функции (№7 ЕГЭ)
Нахождение свойств производной по графику функции (№7 ЕГЭ) Теорема Пифагора
Теорема Пифагора Дифференциал функции. Исследование функции с помощью производной
Дифференциал функции. Исследование функции с помощью производной Комбинаторные задачи
Комбинаторные задачи Многоугольники
Многоугольники Соотношение между сторонами и углами в прямоугольном треугольнике
Соотношение между сторонами и углами в прямоугольном треугольнике Задачи о мобильном интернете и тарифе
Задачи о мобильном интернете и тарифе Простейшие вероятностные задачи
Простейшие вероятностные задачи Состав чисел от 11 до 18. Засели домики (игра-тренажёр) 1 класс
Состав чисел от 11 до 18. Засели домики (игра-тренажёр) 1 класс Аксиомы стереометрии (10 класс)
Аксиомы стереометрии (10 класс) Треугольник . Класс коррекции. 7 класс
Треугольник . Класс коррекции. 7 класс Построение эскизов кривых в декартовых координатах. (Семинар 3)
Построение эскизов кривых в декартовых координатах. (Семинар 3) Расчет показателей надежности систем с нелинейной схемой расчета надежности. Практика 3
Расчет показателей надежности систем с нелинейной схемой расчета надежности. Практика 3 Решение задач по теме: «Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике»
Решение задач по теме: «Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике» Презентация на тему Сравнение отрезков и углов
Презентация на тему Сравнение отрезков и углов Концепция риска. Оценка безопасности
Концепция риска. Оценка безопасности Алгоритмы и структуры данных. Быстрый поиск. Деревья поиска
Алгоритмы и структуры данных. Быстрый поиск. Деревья поиска Три подхода к построению множества целых неотрицательных чисел. Часть 4
Три подхода к построению множества целых неотрицательных чисел. Часть 4 Упражнения для подготовки к ОГЭ по математике, задание №8
Упражнения для подготовки к ОГЭ по математике, задание №8 Софизм - умышленно ложное умозаключение
Софизм - умышленно ложное умозаключение