Содержание
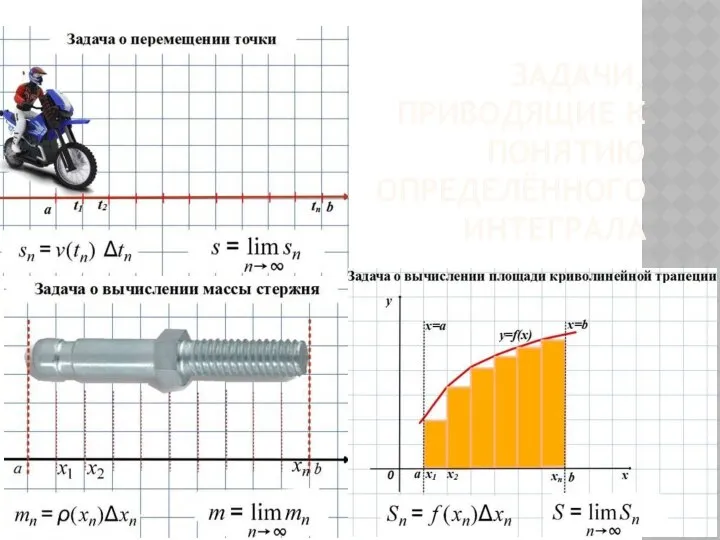
- 2. ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
- 3. Для функции y=f(x) на отрезке [a;b]: Разбить отрезок [a;b] на n равных частей Составить сумму Sn
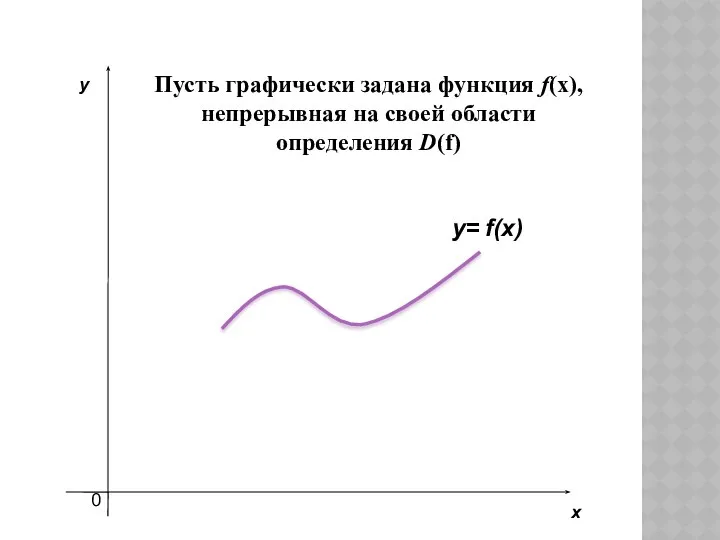
- 4. Пусть графически задана функция f(x), непрерывная на своей области определения D(f) y
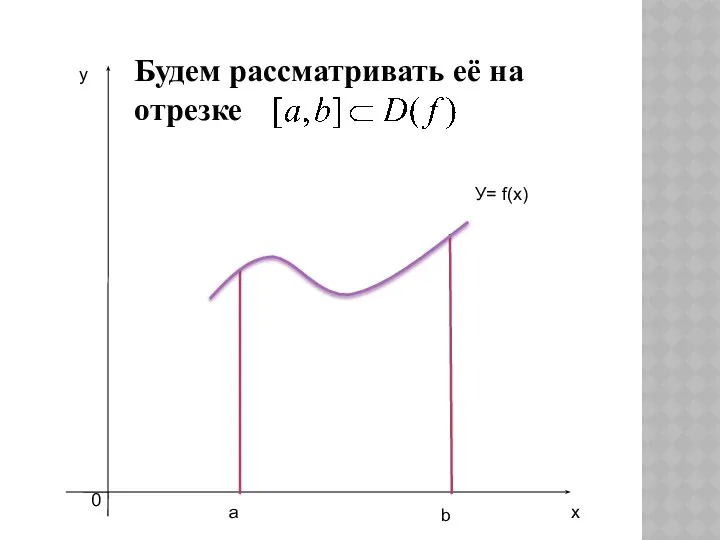
- 5. Будем рассматривать её на отрезке y а b
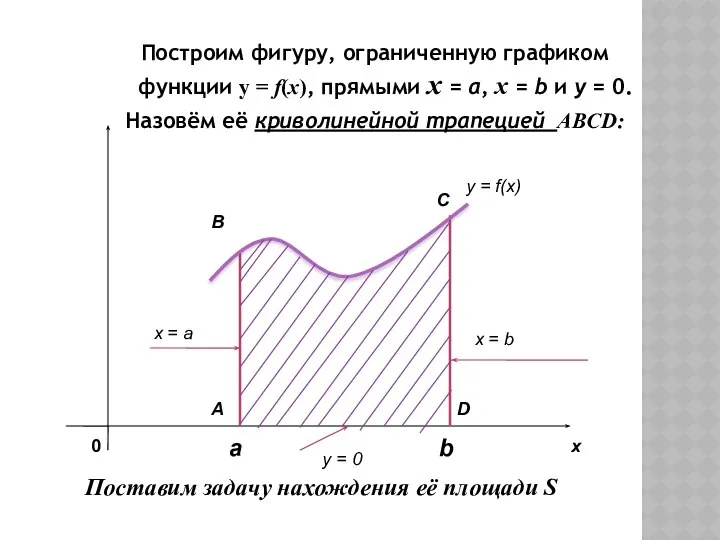
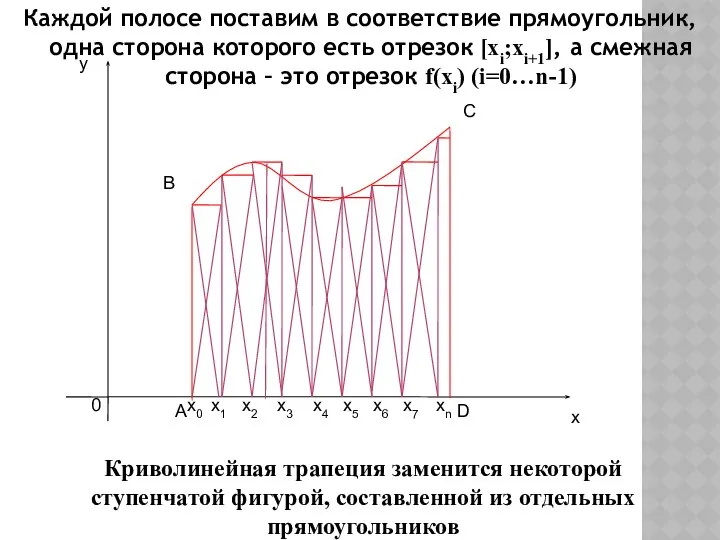
- 6. Построим фигуру, ограниченную графиком функции y = f(x), прямыми x = а, x = b и
- 7. Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a Через точки деления проведём прямые
- 8. Каждой полосе поставим в соответствие прямоугольник, одна сторона которого есть отрезок [xi;xi+1], а смежная сторона –
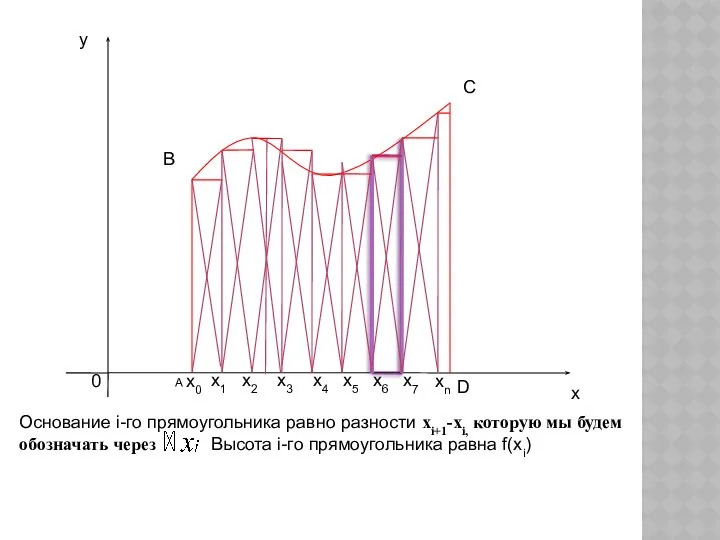
- 9. Основание i-го прямоугольника равно разности xi+1-хi, которую мы будем обозначать через Высота i-го прямоугольника равна f(xi)
- 10. Площадь i-го прямоугольника равна: Сложив площади всех прямоугольников, получаем приближенное значение площади S криволинейной трапеции:
- 11. Точное значение площади S получается как предел суммы площадей всех прямоугольников Для обозначения предельных сумм вида
- 12. Если предел функции f(x) существует, то f(x) называется интегрируемой на отрезке [a, b]. Числа а и
- 14. Определенный интеграл не зависит от выбора первообразной для интегрирования функции. Теорема. Теорема. Для всякой, непрерывной на
- 15. Свойства определенного интеграла Пусть на отрезке существует определенный интеграл где
- 16. 4. Константу как множитель можно выносить за знак определенного интеграла. 5. Определенный интеграл от суммы конечного
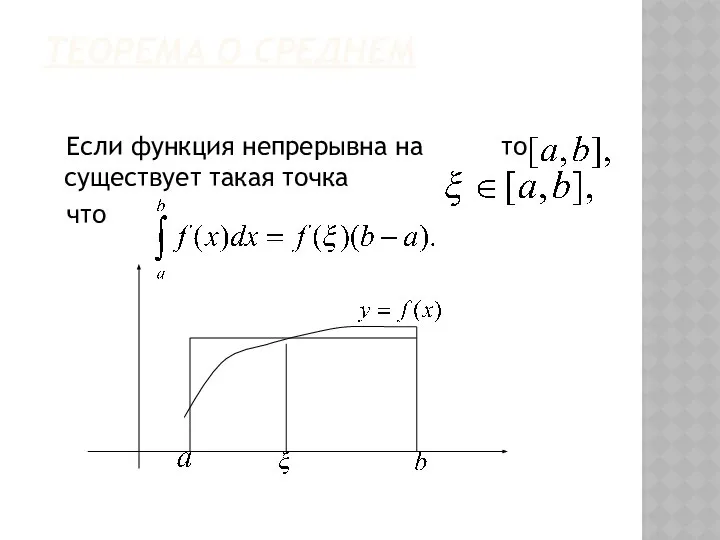
- 17. 6. Если подынтегральная функция неотрицательна, то и определенный интеграл от нее неотрицателен. 7. Теорема о среднем
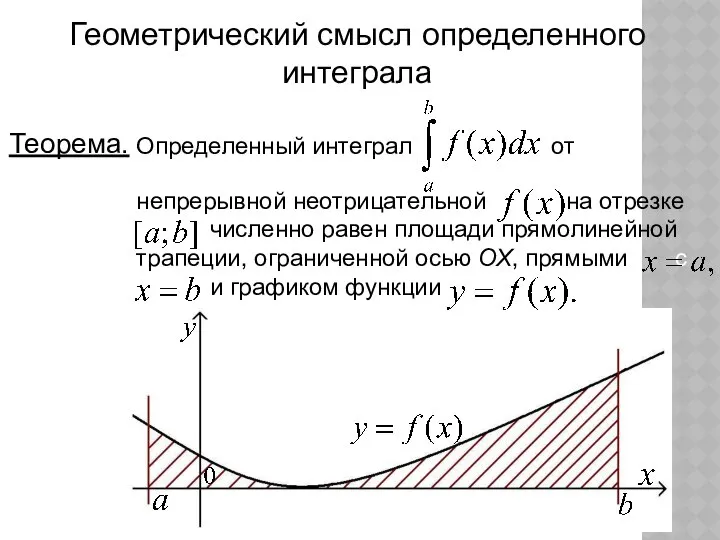
- 18. Геометрический смысл определенного интеграла Теорема. Определенный интеграл от непрерывной неотрицательной на отрезке и численно равен площади
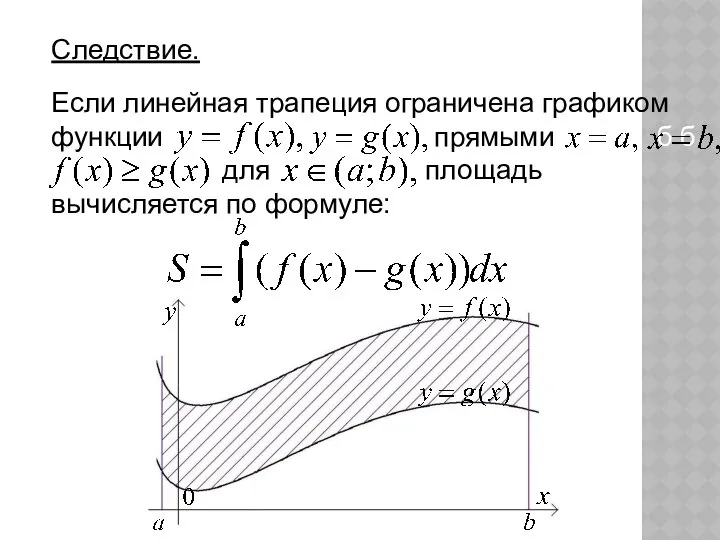
- 19. Следствие. Если линейная трапеция ограничена графиком функции прямыми б б б б для площадь вычисляется по
- 20. Связь и отличие определенных и неопределенных интегралов Связь: Как в неопределенном, так и в определенном интеграле
- 21. Отличие: Неопределенный интеграл – общее выражение для всех первообразных, определенный интеграл – это число.
- 22. ТЕОРЕМА О СУЩЕСТВОВАНИИ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 23. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 24. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 25. ТЕОРЕМА О СРЕДНЕМ Если функция непрерывна на то существует такая точка что
- 26. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 27. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
- 28. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
- 29. ПРИМЕР Вычислить .
- 30. ВЫЧИСЛЕНИЕ ИНТЕГРАЛА
- 31. Теорема. Дано: Введем новую переменную, связанную с формулой b непрерывна на отрезке при этом
- 32. тогда
- 33. ПРИМЕР
- 35. ПРИМЕР
- 36. НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
- 37. ПРИМЕР . Вычислить несобственный интеграл (или установить его расходимость) . Этот несобственный интеграл расходится.
- 38. ПРИМЕР Несобственный интеграл
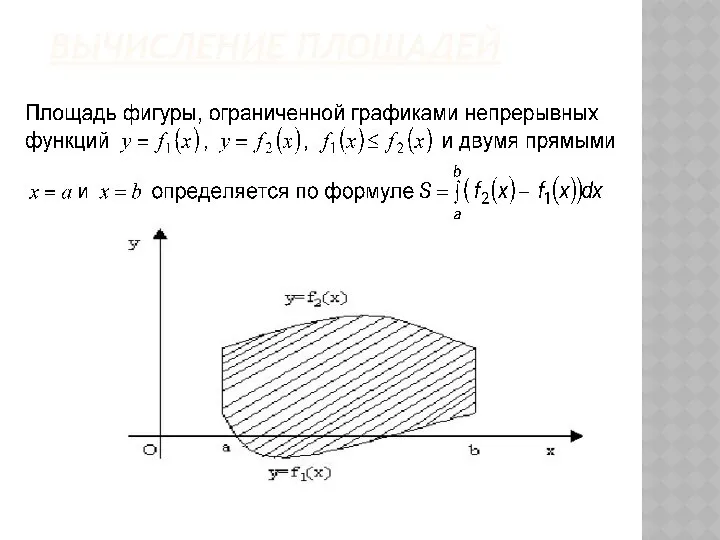
- 39. 1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ Площадь фигуры в декартовых координатах: Геометрические приложения определенного интеграла
- 40. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
- 41. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ В случае параметрического задания кривой, площадь фигуры, ограниченной прямыми , осью Ох и кривой
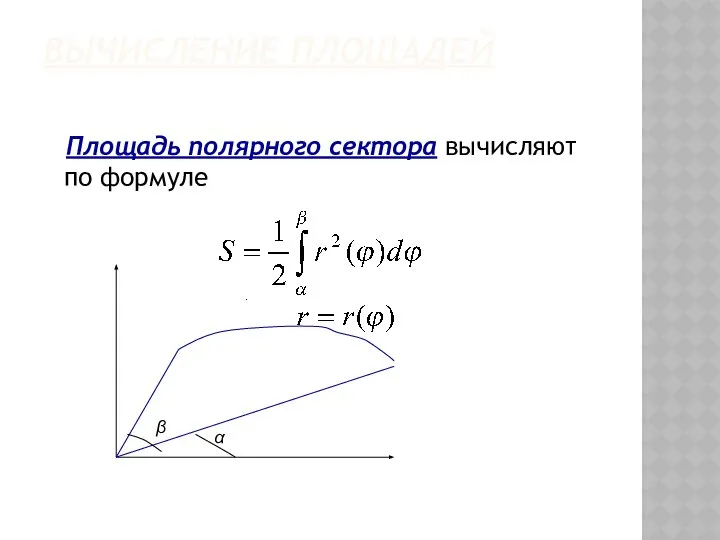
- 42. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ Площадь полярного сектора вычисляют по формуле . α β
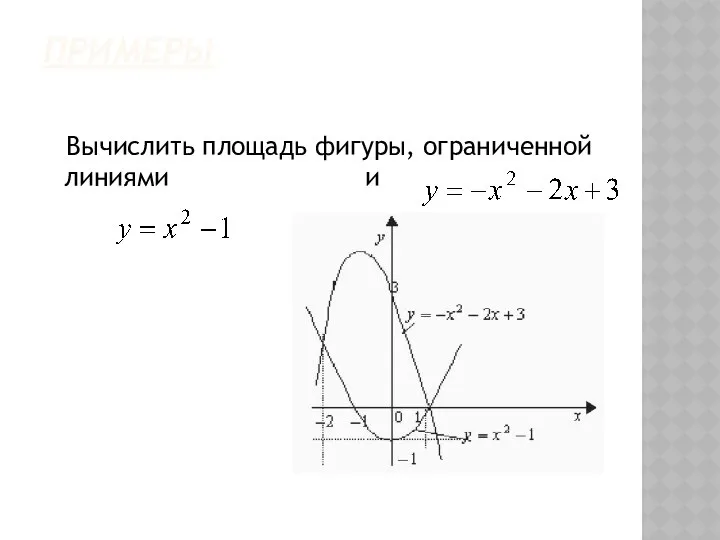
- 43. ПРИМЕРЫ Вычислить площадь фигуры, ограниченной линиями и
- 44. ПРОДОЛЖЕНИЕ Получим
- 45. ПРИМЕРЫ Найти площадь эллипса . Параметрические уравнения эллипса
- 46. ПРИМЕР Площадь фигуры, ограниченной лемнискатой Бернулли и лежащей вне круга радиуса :
- 47. ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ Если кривая задана параметрическими уравнениями , , то длина ее дуги , где
- 48. ДЛИНА ДУГИ В ДЕКАРТОВЫХ КООРДИНАТАХ Если кривая задана уравнением , то , где a, b–абсциссы начала
- 49. ДЛИНА ДУГИ В ПОЛЯРНЫХ КООРДИНАТАХ Если кривая задана уравнением в полярных координатах , то , где
- 50. ПРИМЕРЫ Вычислить длину дуги кривой от точки до . , тогда
- 51. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА ВРАЩЕНИЯ. Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой ,
- 52. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА ВРАЩЕНИЯ Объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной кривой , отрезком
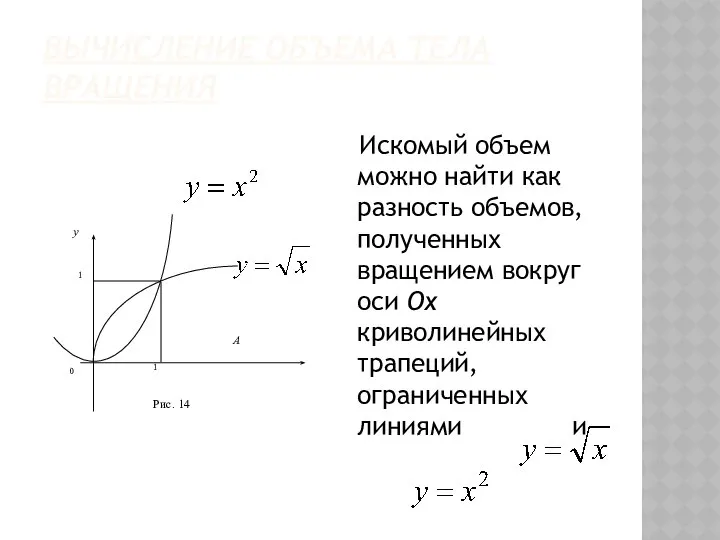
- 53. ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА ВРАЩЕНИЯ Искомый объем можно найти как разность объемов, полученных вращением вокруг оси Ox
- 55. Скачать презентацию
![Для функции y=f(x) на отрезке [a;b]: Разбить отрезок [a;b] на n](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1440001/slide-2.jpg)
![Разделим основание [АD] трапеции ABCD точками х0=а;х1;х2;…; хn= b (x0= a](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1440001/slide-6.jpg)











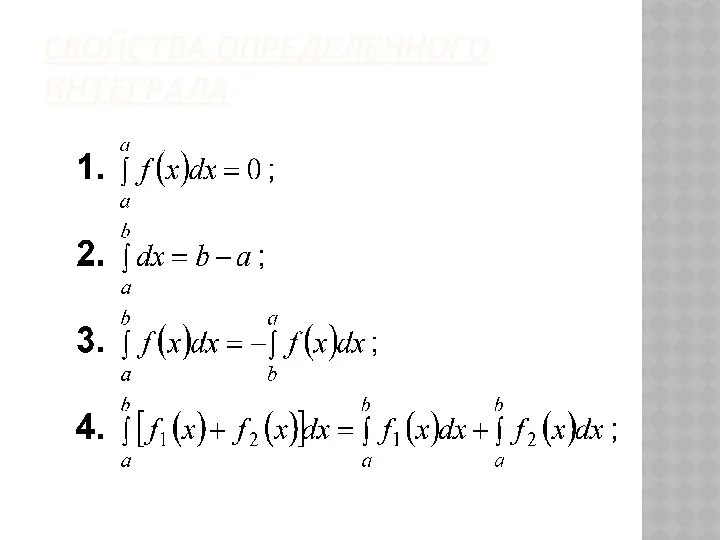




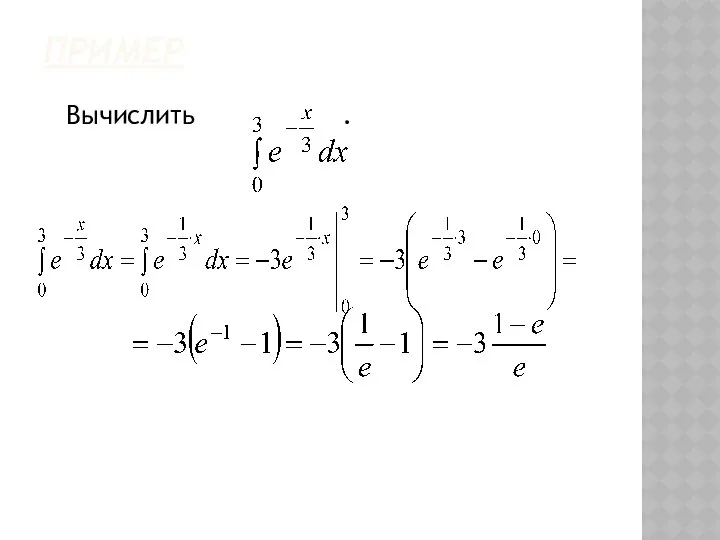


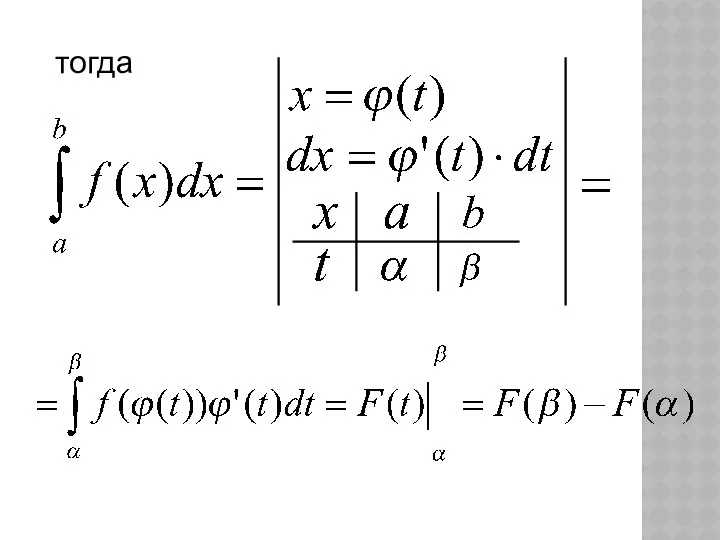
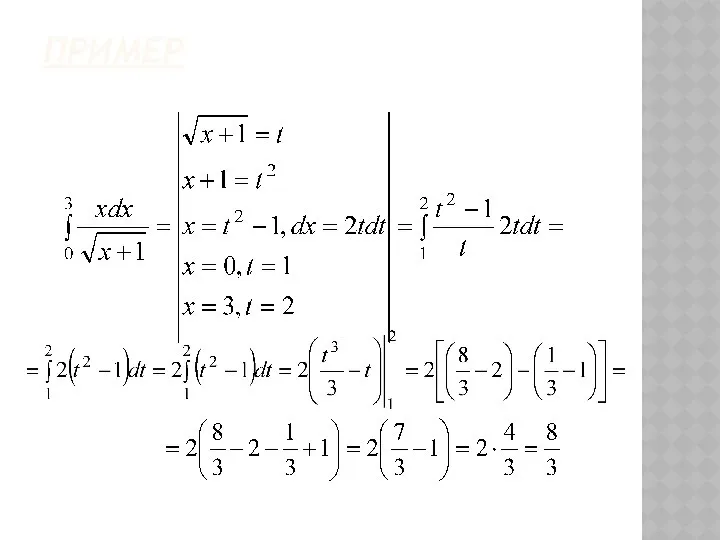

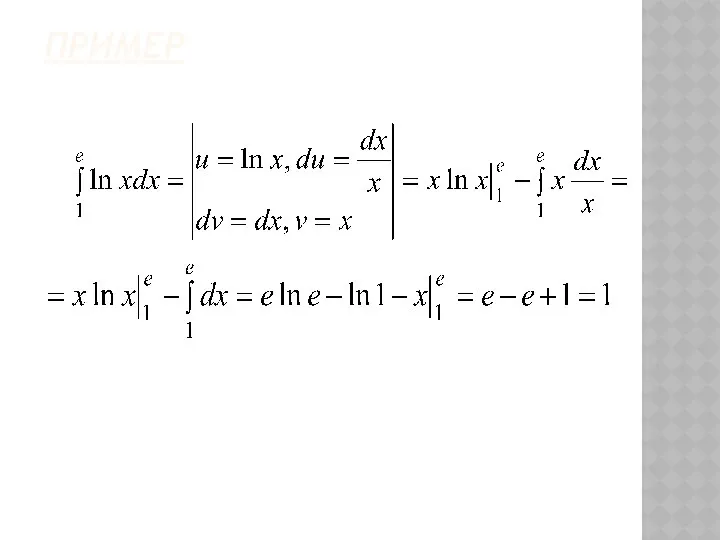


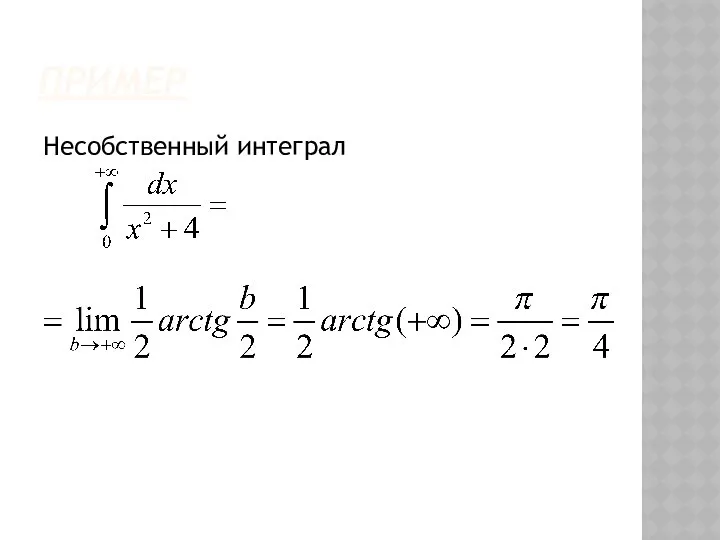











 Тест по геометрии, 8 класс
Тест по геометрии, 8 класс Решение системы неравенств
Решение системы неравенств Узы дружбы в мире чисел. Исследовательская работа. 9 класс
Узы дружбы в мире чисел. Исследовательская работа. 9 класс Внеклассное мероприятие по математике в 5 классе
Внеклассное мероприятие по математике в 5 классе Комбинаторика. Теория вероятности
Комбинаторика. Теория вероятности Степенная функция
Степенная функция Функция. Основные понятия
Функция. Основные понятия Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам)
Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам) Тригонометрические неравенства
Тригонометрические неравенства Задачи. 5 класс
Задачи. 5 класс Цифры и числа первого десятка, 1 класс
Цифры и числа первого десятка, 1 класс Направления и лучи
Направления и лучи Усеченный конус
Усеченный конус Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Решение линейных неравенств. 8 класс
Решение линейных неравенств. 8 класс Методы исследования математических моделей
Методы исследования математических моделей Численное интегрирование. Квадратурные формулы
Численное интегрирование. Квадратурные формулы Число 9. Цифра 9. Занятие 21
Число 9. Цифра 9. Занятие 21 Теорема об отрезках пересекающихся хорд (8 класс)
Теорема об отрезках пересекающихся хорд (8 класс) Пассивный и активный эксперимент
Пассивный и активный эксперимент Задача предельного типа. Мир арифметики
Задача предельного типа. Мир арифметики Преобразование логарифмических выражений
Преобразование логарифмических выражений Решение тригонометрических уравнений
Решение тригонометрических уравнений УРОК МАТЕМАТИКИ 6 КЛАСС «Нахождение числа по его дроби»
УРОК МАТЕМАТИКИ 6 КЛАСС «Нахождение числа по его дроби»  Круг и окружность
Круг и окружность Презентация по математике "Проценты" - скачать бесплатно_
Презентация по математике "Проценты" - скачать бесплатно_ Нахождение дроби от числа и процентов от числа.
Нахождение дроби от числа и процентов от числа. Потреба у паліативній допомозі в Україні: розбіжності у статистичних даних
Потреба у паліативній допомозі в Україні: розбіжності у статистичних даних