Содержание
- 2. План лекции: Место и роль математики в современном мире, мировой культуре и истории. Понятие функции. Способы
- 3. Понятие функции Слово «функция» (от латинского «Functio» - исполнение обязанностей, деятельность) впервые ввел немецкий ученый Г.
- 4. Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной у, то
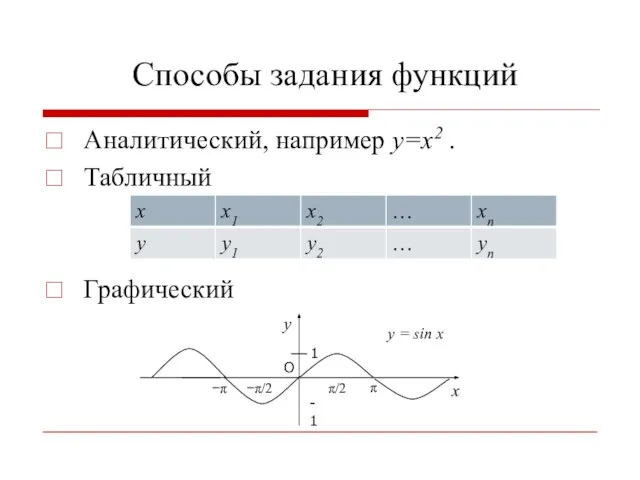
- 5. Способы задания функций Аналитический, например у=х2 . Табличный Графический
- 6. Четность и нечетность Функция y = f(x) называется четной, если для любого значения x, взятого из
- 7. Функция y = f(x) называется нечетной, если для любого значения x, взятого из области определения функции,
- 8. При построении графиков четной и нечетной функции достаточно построить только правую ветвь графика для положительных значений
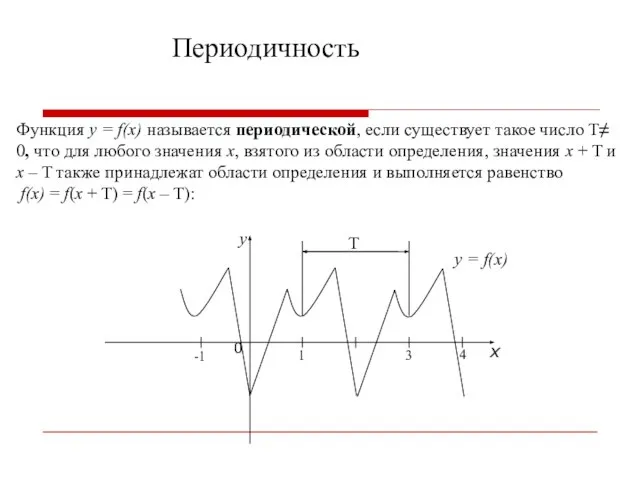
- 9. Периодичность Функция y = f(x) называется периодической, если существует такое число T≠ 0, что для любого
- 10. Число T называется периодом функции. Всякая периодическая функция имеет бесконечное число периодов. Числа вида nT при
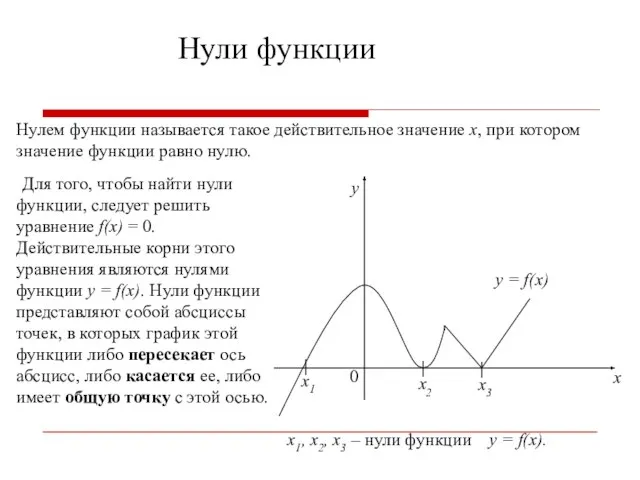
- 11. Нули функции Нулем функции называется такое действительное значение x, при котором значение функции равно нулю. Для
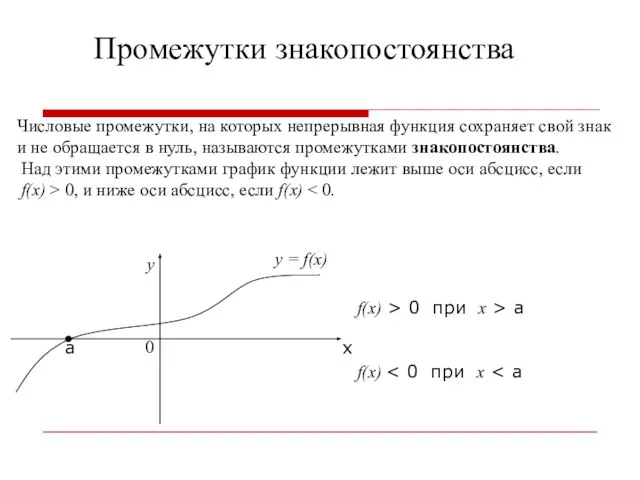
- 12. Промежутки знакопостоянства Числовые промежутки, на которых непрерывная функция сохраняет свой знак и не обращается в нуль,
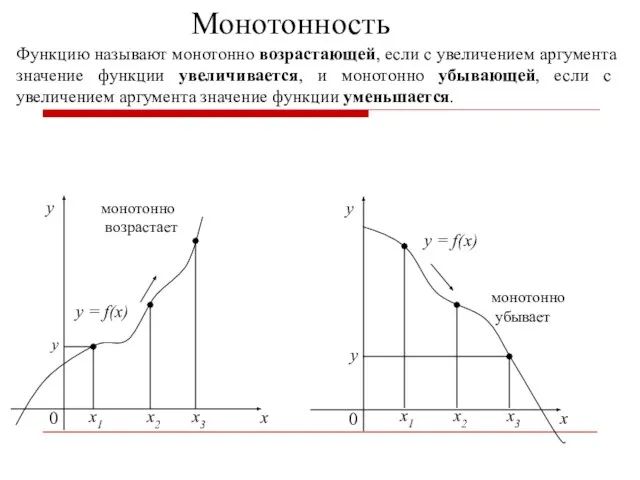
- 13. Монотонность Функцию называют монотонно возрастающей, если с увеличением аргумента значение функции увеличивается, и монотонно убывающей, если
- 14. Функция y = f(x) называется монотонно возрастающей на интервале (a, b), если для любых x1 и
- 15. Понятие обратной функции Функция, принимающая каждое свое значение в единственной точке области определения, называется обратимой. Таким
- 16. Экстремумы функции. Наибольшее и наименьшее значение функции Точка x0 называется точкой максимума (точкой минимума) для функции
- 17. Пусть функция y = f(x) определена на отрезке[a; b]. Говорят, что функция имеет максимум в точке
- 18. Пусть функция y = f(x) определена на отрезке [a; b]. Говорят, что функция имеет минимум в
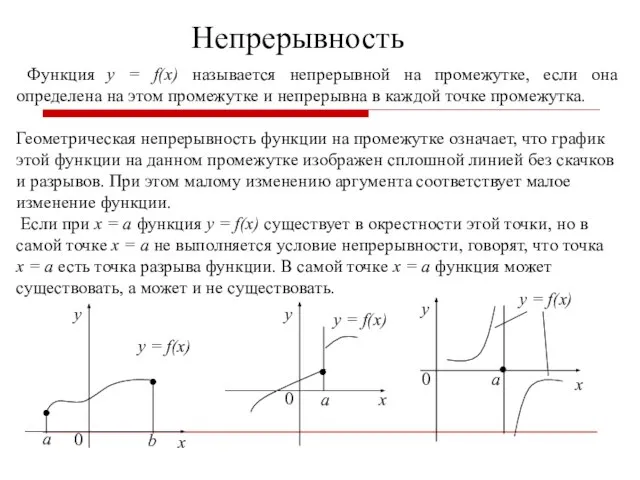
- 19. Непрерывность Функция y = f(x) называется непрерывной на промежутке, если она определена на этом промежутке и
- 20. Элементарные функции Линейная Обратная пропорциональность Степенная Показательная Логарифмическая Тригонометрические
- 21. Линейная функция Функция вида y = kx + b, где k и b некоторые числа, называется
- 22. 2. Если b = 0, то y = kx. Линейная функция вида y = kx называется
- 23. Коэффициенты k и b в уравнении линейной функции y = kx + b, имеют наглядное геометрическое
- 24. Обратная пропорциональность Гипербола - график функции . При а > 0 расположена в I и III
- 25. Степенная функция Функция вида . Пример – парабола. Парабола - график функции квадратного трёхчлена у =
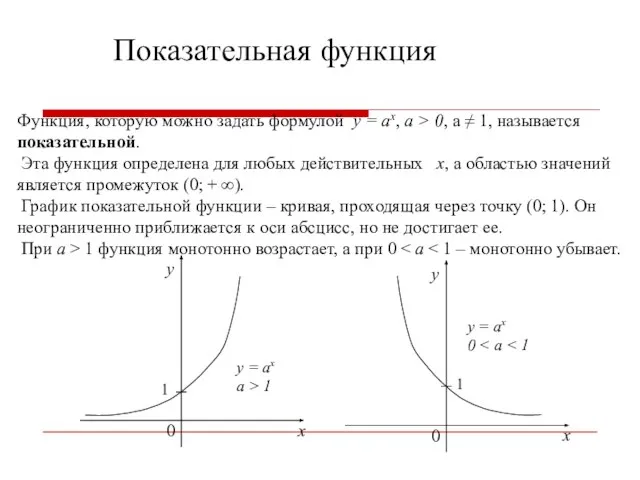
- 26. Показательная функция Функция, которую можно задать формулой y = ax, a > 0, a ≠ 1,
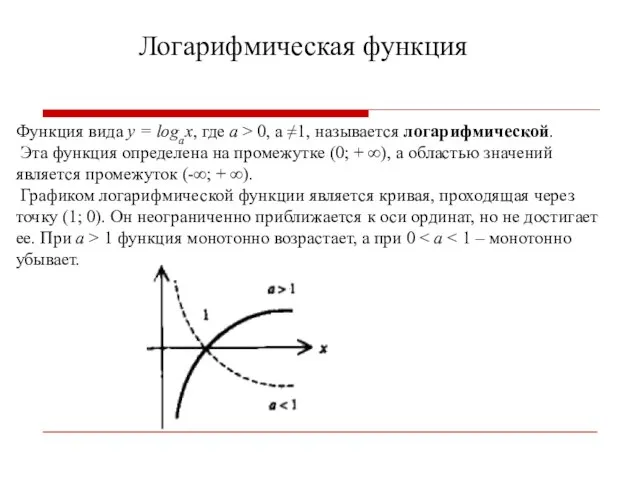
- 27. Логарифмическая функция Функция вида y = logax, где a > 0, a ≠1, называется логарифмической. Эта
- 28. Тригонометрические функции 1.Функция синус (y = sin x) Функция определена и непрерывна на всем множестве действительных
- 29. 2.Функция косинус (y = cos x) Функция определена и непрерывна на всем множестве действительных чисел. Эта
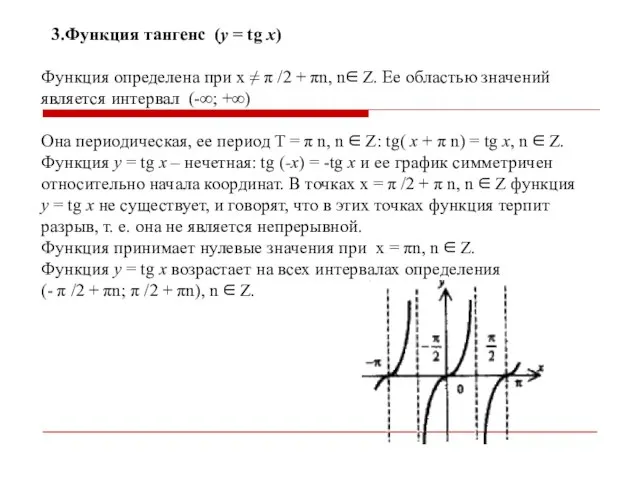
- 30. 3.Функция тангенс (y = tg x) Функция определена при x ≠ π /2 + πn, n∈
- 31. 4.Функция котангенс (y = ctg x) Функция определена при x ≠ πn, n∈ Z. Ее областью
- 32. Домашнее задание 1. Найти область определения функций: ;
- 33. Домашнее задание 2. Найти множество значений функций: у = х2– 6х+5; у = 3 + 2sinx;
- 34. Домашнее задание 4. Функция задана в виде . Найти: 1) у (-х); 2) у (kх); 3)
- 36. Скачать презентацию










![Пусть функция y = f(x) определена на отрезке[a; b]. Говорят, что](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/600889/slide-16.jpg)
![Пусть функция y = f(x) определена на отрезке [a; b]. Говорят,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/600889/slide-17.jpg)












 Ипотека : математика в экономике (математика вокруг нас). 10кл (1)
Ипотека : математика в экономике (математика вокруг нас). 10кл (1) Метод рационализации. Задание 15, ЕГЭ
Метод рационализации. Задание 15, ЕГЭ Построение и преобразование графиков квадратичной функции. Графические возможности Excel
Построение и преобразование графиков квадратичной функции. Графические возможности Excel Презентация по математике "История: Математики и Геометрии" - скачать
Презентация по математике "История: Математики и Геометрии" - скачать  Математика в мире животных
Математика в мире животных Презентация на тему Число и цифра 8
Презентация на тему Число и цифра 8 Решение логических задач
Решение логических задач Золотое сечение
Золотое сечение Подготовка к ГИА. Демоверсия 2013
Подготовка к ГИА. Демоверсия 2013 Сложение и вычитание
Сложение и вычитание Решение задач на смеси и сплавы (арифметический способ)
Решение задач на смеси и сплавы (арифметический способ) Две окружности на плоскости
Две окружности на плоскости Решение задач по теме «Четырехугольники»
Решение задач по теме «Четырехугольники» Інтегральне числення. Елементи інтегрального числення (лекція 2)
Інтегральне числення. Елементи інтегрального числення (лекція 2) Элементы комбинаторики в электроснабжении
Элементы комбинаторики в электроснабжении Комплексные числа
Комплексные числа Математика 4 класс Морозова Валентина Анатольевна учитель начальных классов МОУ Шевыряловская основная общеобразовательная шк
Математика 4 класс Морозова Валентина Анатольевна учитель начальных классов МОУ Шевыряловская основная общеобразовательная шк Метод координат при решении стереометрических задач. Урок геометрии, 11 класс
Метод координат при решении стереометрических задач. Урок геометрии, 11 класс Теория вероятностей. Математическая статистика
Теория вероятностей. Математическая статистика Презентация на тему Округление натуральных чисел 5 класс
Презентация на тему Округление натуральных чисел 5 класс Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем
Использование метода ЛАЧХ для синтеза регуляторов манипулятора с гибким стержнем Площадь параллелограмма, треугольника и трапеции. Урок 19
Площадь параллелограмма, треугольника и трапеции. Урок 19 Корреляцияның параметрлік емес бағалау әдісі
Корреляцияның параметрлік емес бағалау әдісі Вычисления с рациональными числами
Вычисления с рациональными числами Решение задач. Закрепление пройденного
Решение задач. Закрепление пройденного Действия с десятичными дробями
Действия с десятичными дробями Презентация по математике "Диаграммы" - скачать
Презентация по математике "Диаграммы" - скачать  Симметрия в технике
Симметрия в технике