Содержание
- 2. I. Основные понятия Статистика – это область науки, изучающая сбор, анализ и интерпретацию данных. От лат.
- 3. Пример 1. В девятых классах «А» и «Б» измерили рост 50 учеников. Получились следующие результаты: 162,
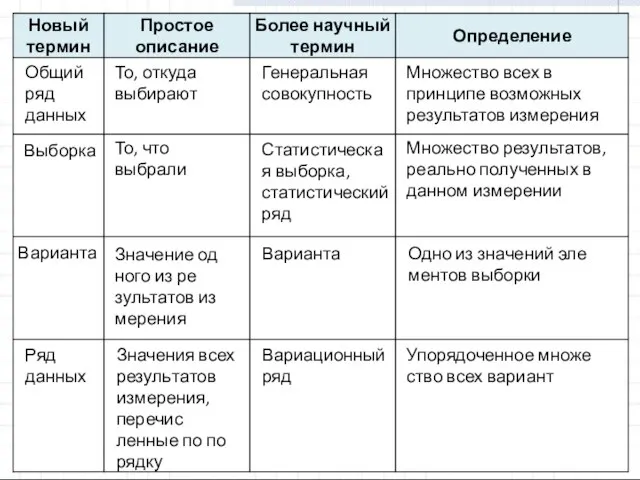
- 4. Общий ряд данных Выборка Варианта Ряд данных То, откуда выбирают То, что выбрали Значение одного из
- 5. Пример 1. В девятых классах «А» и «Б» измерили рост 50 учеников. Получились следующие результаты: 162,
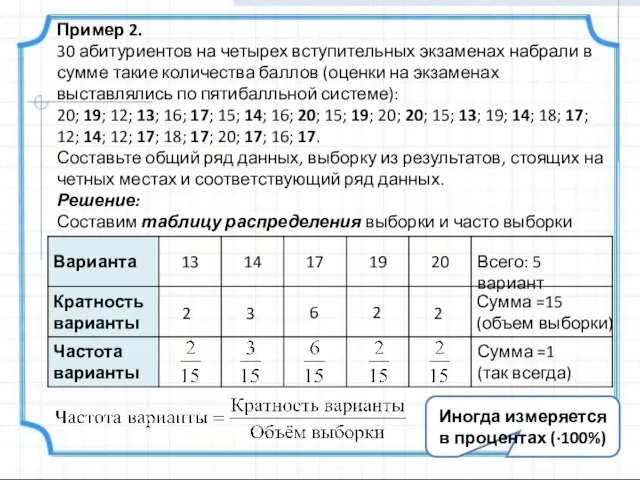
- 6. Пример 2. 30 абитуриентов на четырех вступительных экзаменах набрали в сумме такие количества баллов (оценки на
- 7. Пример 2. 30 абитуриентов на четырех вступительных экзаменах набрали в сумме такие количества баллов (оценки на
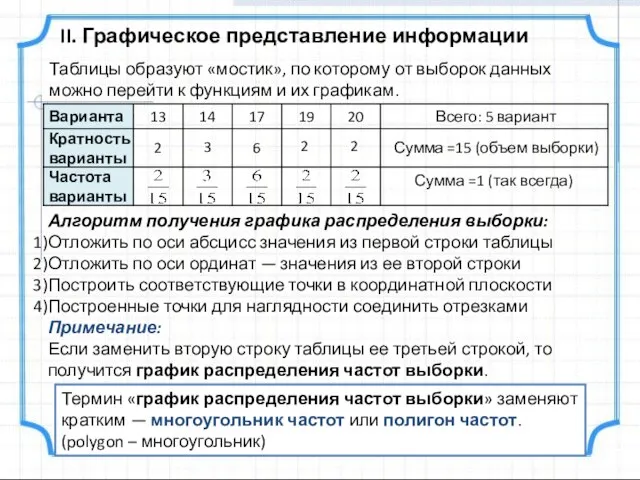
- 8. II. Графическое представление информации Алгоритм получения графика распределения выборки: Отложить по оси абсцисс значения из первой
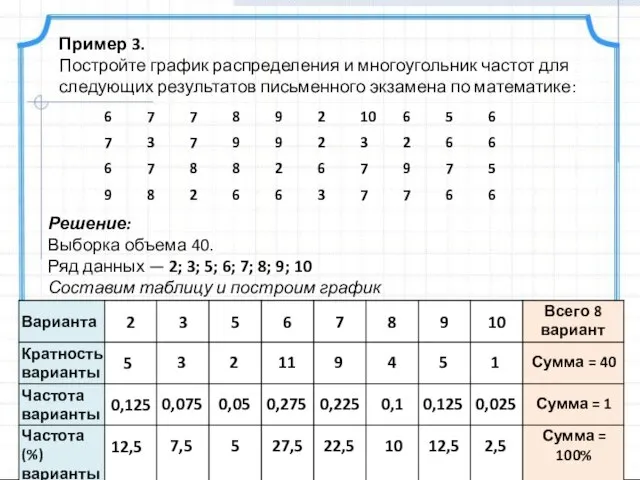
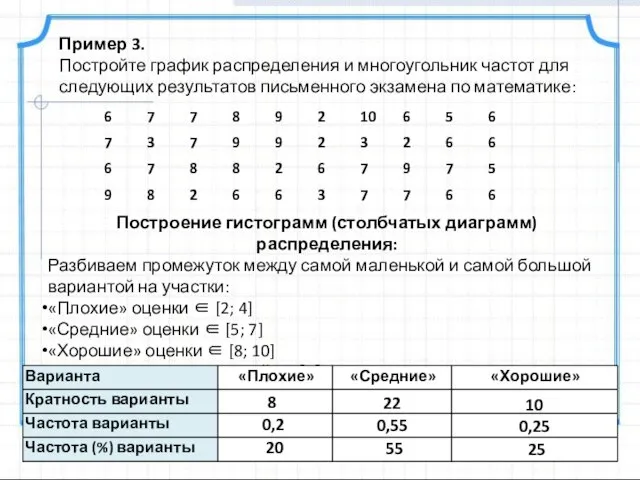
- 9. Пример 3. Постройте график распределения и многоугольник частот для следующих результатов письменного экзамена по математике: Решение:
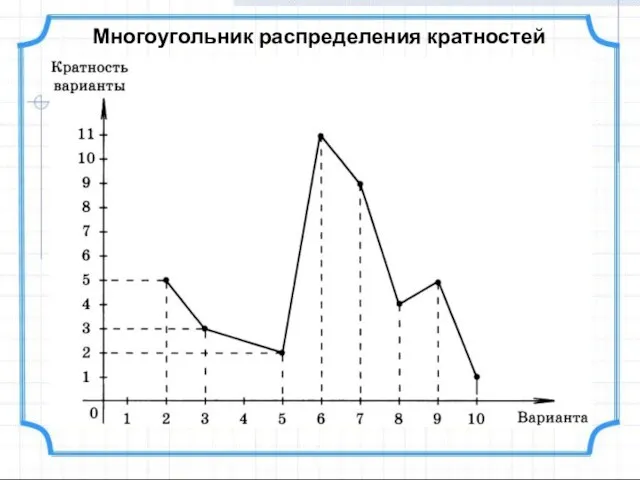
- 10. Многоугольник распределения кратностей
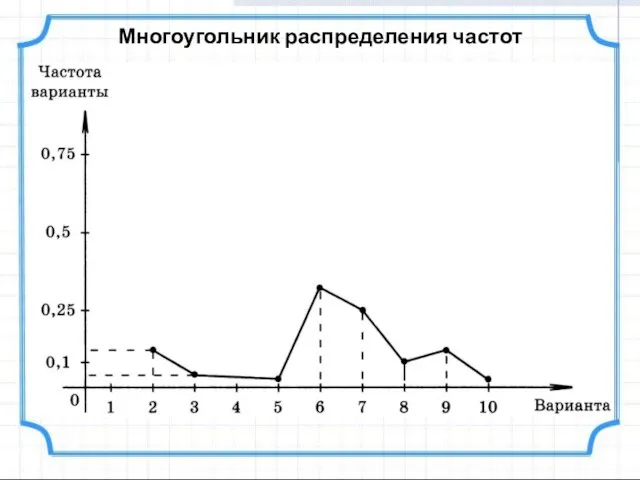
- 11. Многоугольник распределения частот
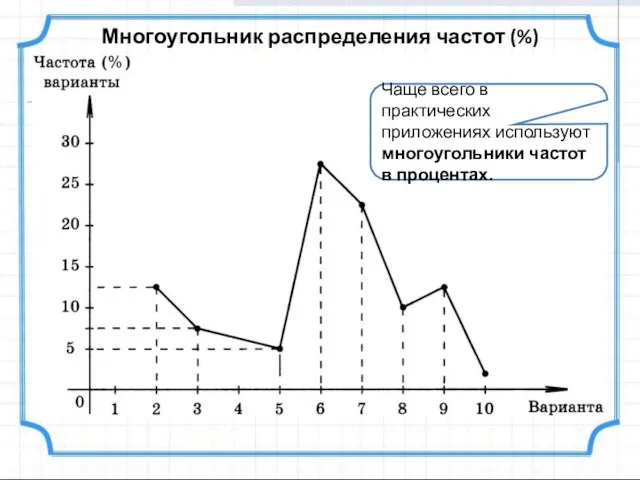
- 12. Многоугольник распределения частот (%) Чаще всего в практических приложениях используют многоугольники частот в процентах.
- 13. Построение гистограмм (столбчатых диаграмм) распределения: Разбиваем промежуток между самой маленькой и самой большой вариантой на участки:
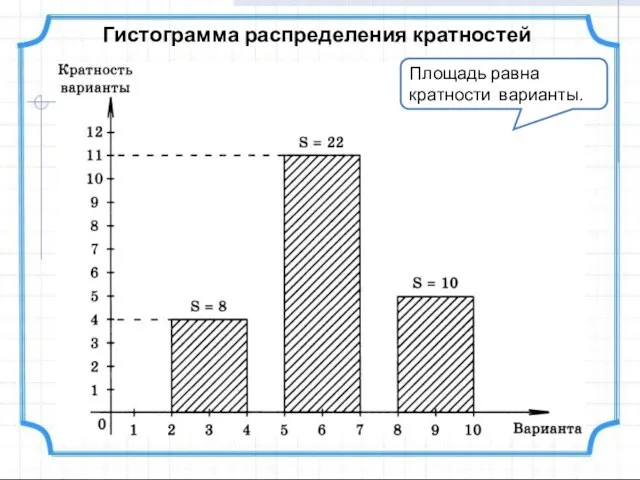
- 14. Гистограмма распределения кратностей Площадь равна кратности варианты.
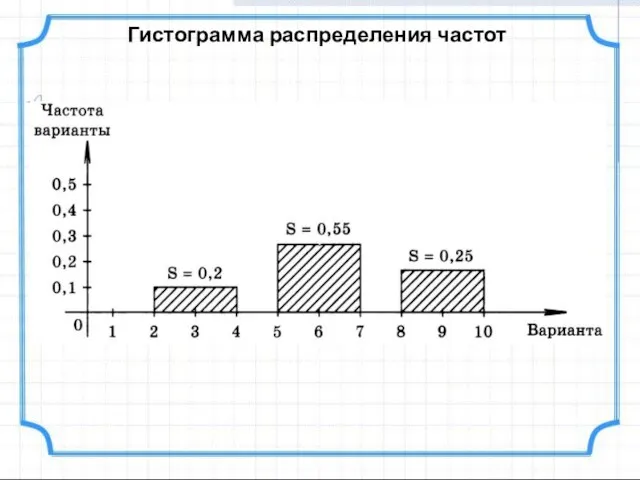
- 15. Гистограмма распределения частот
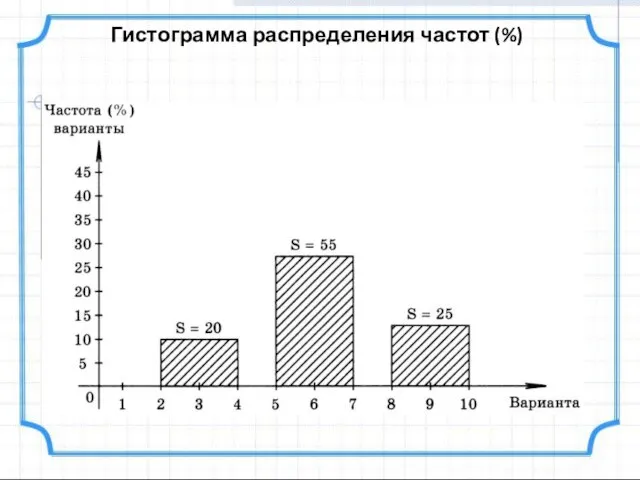
- 16. Гистограмма распределения частот (%)
- 17. «-» представления информации в виде гистограмм Теряется первоначальная точная информация «+» Ответ получается более быстро Наглядно
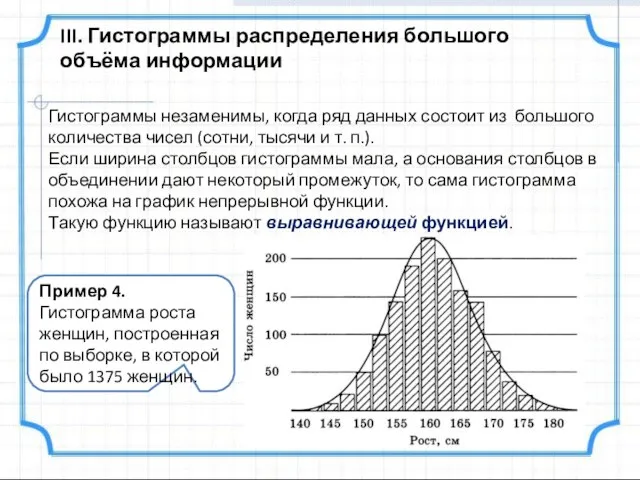
- 18. III. Гистограммы распределения большого объёма информации Гистограммы незаменимы, когда ряд данных состоит из большого количества чисел
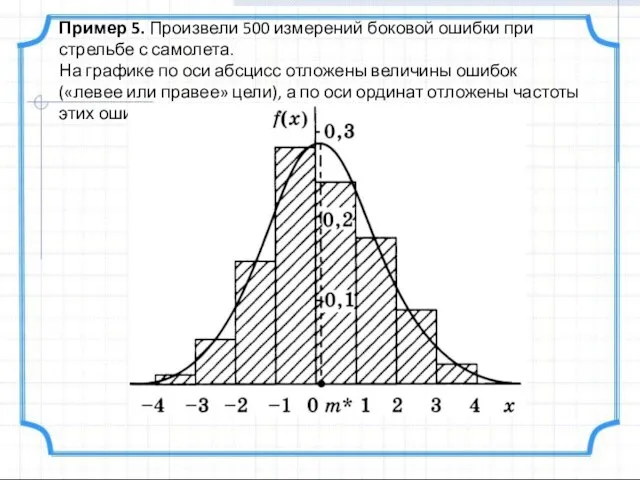
- 19. Пример 5. Произвели 500 измерений боковой ошибки при стрельбе с самолета. На графике по оси абсцисс
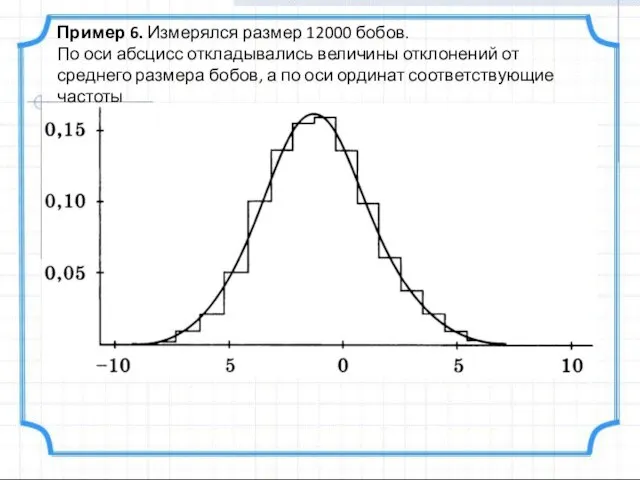
- 20. Пример 6. Измерялся размер 12000 бобов. По оси абсцисс откладывались величины отклонений от среднего размера бобов,
- 21. Примеры взяты из различных областей, а графики функций, выравнивающих гистограммы, похожи друг на друга. Такому же
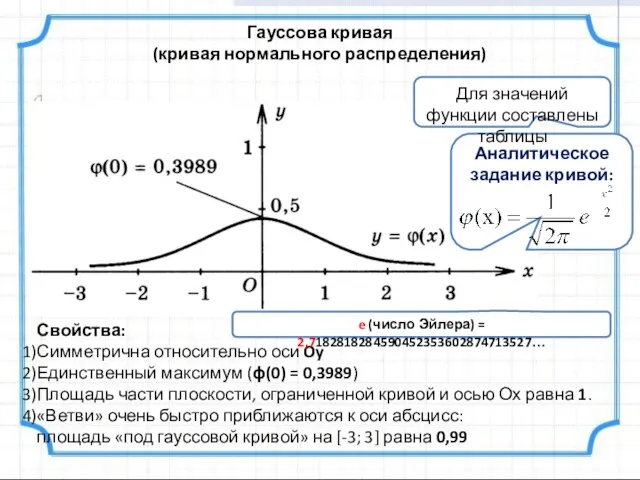
- 22. Гауссова кривая (кривая нормального распределения) Свойства: Симметрична относительно оси Oy Единственный максимум (ϕ(0) = 0,3989) Площадь
- 23. Доска Гальтона (квинкункс, 1873 г.) Устройство для наглядной демонстрации нормального (гауссова) закона распределения Принцип действия: Падающие
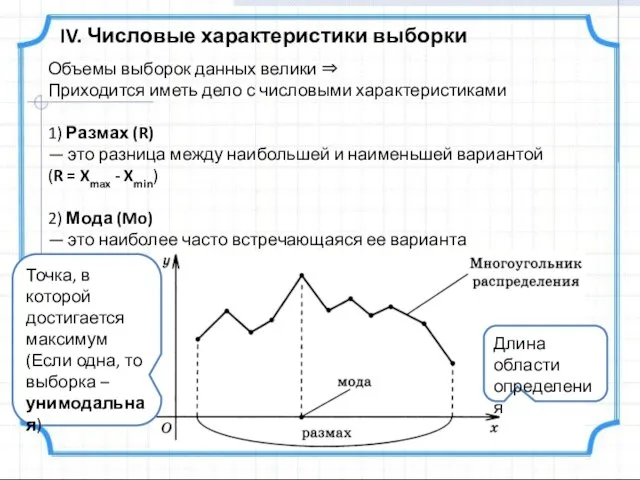
- 24. IV. Числовые характеристики выборки Объемы выборок данных велики ⇒ Приходится иметь дело с числовыми характеристиками 1)
- 26. 3) Медиана (Me) (от лат. mediana – «среднее») Медианой выборки с нечетным числом вариант называется варианта,
- 27. Пример 7. Найдите среднее значение, размах и моду выборки: а) 32; 26; 18; 26; 15; 21;
- 28. Пример 8. В выборке 2, 7, 10, _, 18, 19, 27 одно число оказалось стертым. Восстановите
- 29. Пример 9. Найдите медиану выборки: 30, 32, 37, 40, 41, 42, 45, 49, 52; Пример 10.
- 30. Пример 11. В ряду данных, состоящем из 12 чисел, наибольшее число увеличили на 6. Изменятся ли
- 31. 5) Среднее отклонение ( ) Среднее арифметическое отклонений (в абсолютных показателях) всех вариант выборки от их
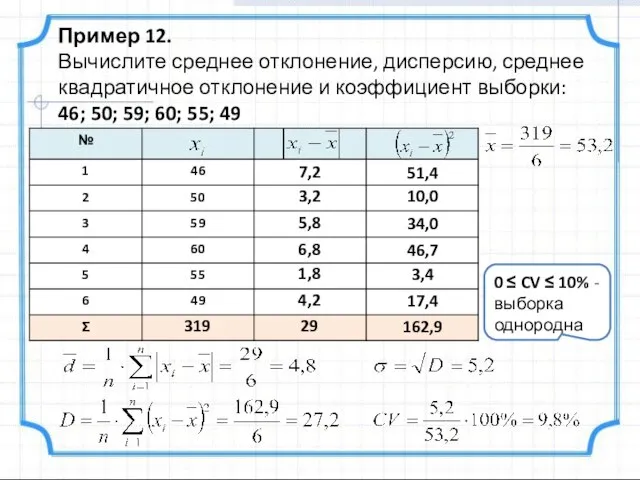
- 32. Пример 12. Вычислите среднее отклонение, дисперсию, среднее квадратичное отклонение и коэффициент выборки: 46; 50; 59; 60;
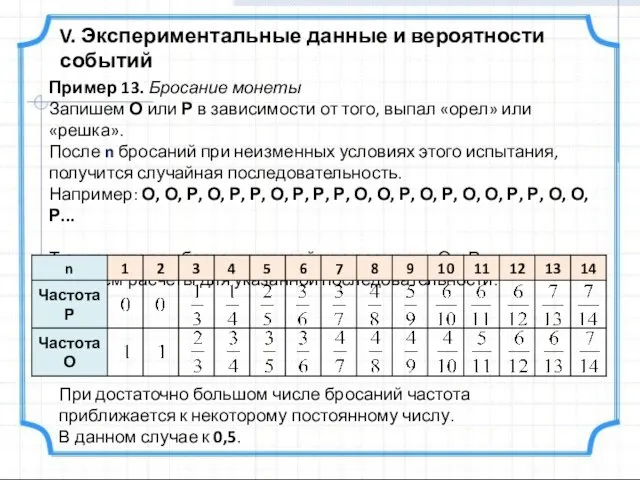
- 33. V. Экспериментальные данные и вероятности событий Пример 13. Бросание монеты Запишем О или Р в зависимости
- 34. Бросил монету 4040 раз, и при этом герб выпал в 2048 случаях. Бросил монету 24000 раз,
- 35. Статистическая устойчивость (СУ) При большом числе независимых повторений одного и того же опыта в неизменных условиях
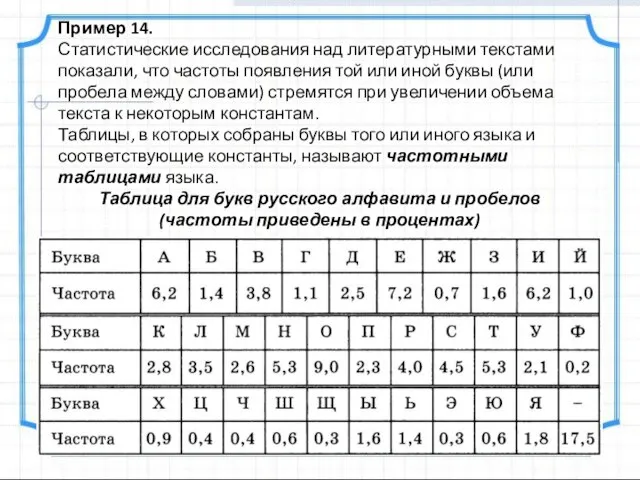
- 36. Пример 14. Статистические исследования над литературными текстами показали, что частоты появления той или иной буквы (или
- 37. Пример 15. До сегодняшнего дня не утихают споры об авторстве «Тихого Дона». Многие считают, что в
- 38. Пример 16. В середине 60-х годов в одной из стран Западной Европы были опубликованы «очерняющие прогрессивный
- 40. Скачать презентацию

















 Аrcsin
Аrcsin Свойства средней арифметической
Свойства средней арифметической Аттестационная работа. Эссе Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС
Аттестационная работа. Эссе Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС Зачетная система в старших классах как средство предупреждения неуспеваемости
Зачетная система в старших классах как средство предупреждения неуспеваемости Интерактивный тренажёр «Осенний». Математика 1 класс. Сложение и вычитание в пределах 5
Интерактивный тренажёр «Осенний». Математика 1 класс. Сложение и вычитание в пределах 5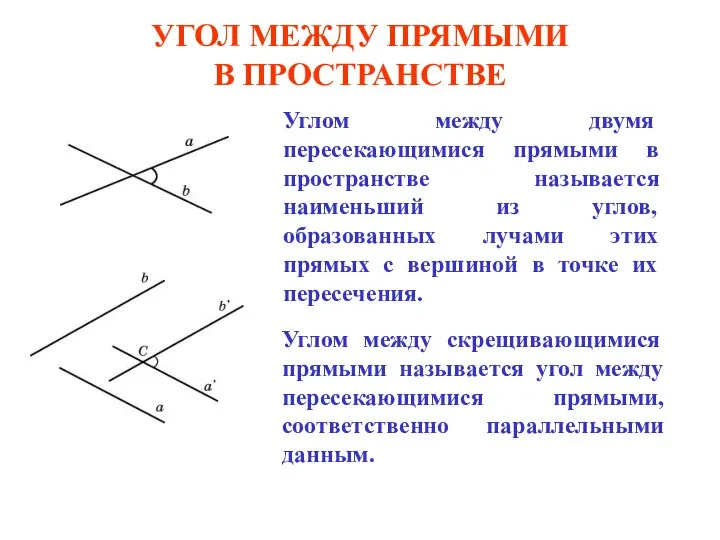 Угол между прямыми в пространстве
Угол между прямыми в пространстве Топологические опыты. Мини-урок
Топологические опыты. Мини-урок Подготовка к ЕГЭ – 2014 по математике. Нахождение площади сечения через площадь его ортогональной проекции. Задание С2
Подготовка к ЕГЭ – 2014 по математике. Нахождение площади сечения через площадь его ортогональной проекции. Задание С2 Теория пределов. Лекция 1
Теория пределов. Лекция 1 Векторы 9 класс
Векторы 9 класс Презентация на тему Уравнения математика 3 класс
Презентация на тему Уравнения математика 3 класс Путешествие в сказку математика
Путешествие в сказку математика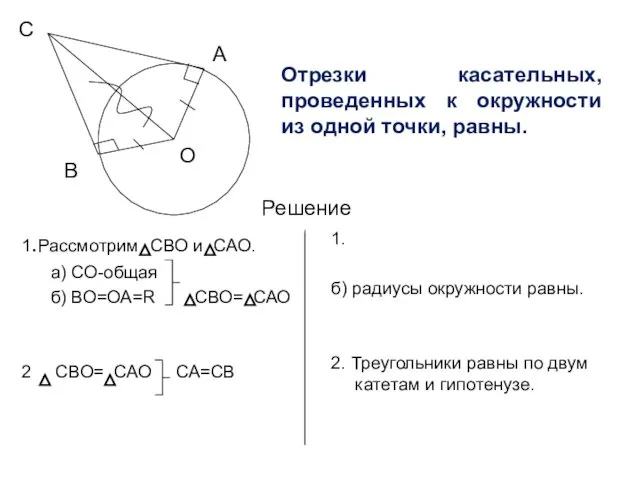 Отрезки касательных, проведенных к окружности из одной точки
Отрезки касательных, проведенных к окружности из одной точки Симметрия в нашей жизни
Симметрия в нашей жизни Правильные многогранники
Правильные многогранники Призма и её элементы. Прямая и правильная призмы
Призма и её элементы. Прямая и правильная призмы Урок математики в 5 классе по учебнику Н.Я.Виленкина, В.И.Жохова, А.С. Чеснокова, С.И.Шварцбурда Учитель: Тихая Наталья Анатольевна, М
Урок математики в 5 классе по учебнику Н.Я.Виленкина, В.И.Жохова, А.С. Чеснокова, С.И.Шварцбурда Учитель: Тихая Наталья Анатольевна, М Неравенства с двумя переменными
Неравенства с двумя переменными Делимость чисел 8 класс - Презентация_
Делимость чисел 8 класс - Презентация_ Раскраска вершин графа. Глава 7
Раскраска вершин графа. Глава 7 Сложение и вычитание дробей
Сложение и вычитание дробей Единицы измерений
Единицы измерений Тема: Плоскость, прямая, луч
Тема: Плоскость, прямая, луч  Путешествие в мир десятичных дробей
Путешествие в мир десятичных дробей Тренажёр «Сложение в пределах 100»
Тренажёр «Сложение в пределах 100» Полный дифференциал функции нескольких переменных. (Лекция 2)
Полный дифференциал функции нескольких переменных. (Лекция 2) Общее повторение алгебры
Общее повторение алгебры Елементи трикутників та чорикутників, їх види. Периметр, сума кутів
Елементи трикутників та чорикутників, їх види. Периметр, сума кутів