Содержание
- 2. 7.1. Постановка задачи
- 3. Постановка задачи Раскраска называется правильной, если никакие две смежные вершины на окрашены в один цвет. Раскраска
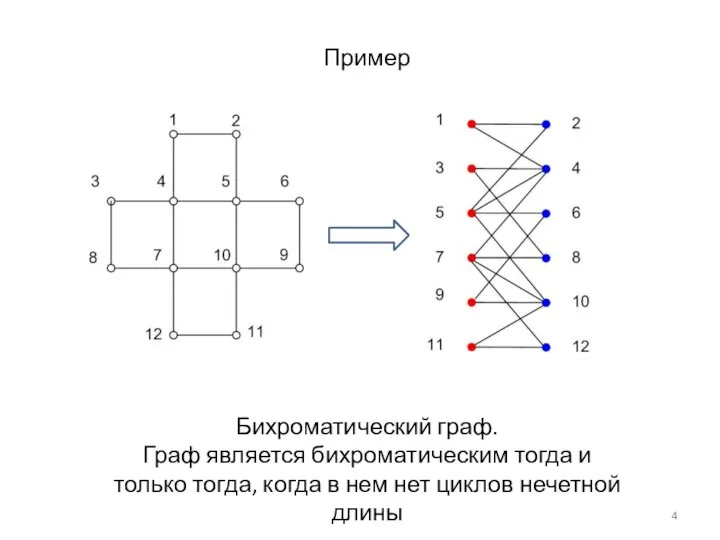
- 4. Бихроматический граф. Граф является бихроматическим тогда и только тогда, когда в нем нет циклов нечетной длины
- 5. Приложения Календарное планирование: вершины соответствуют работам, смежность вершин означает конфликт по использованию ресурсов. Распределение памяти в
- 6. 7.2. Точный алгоритм раскраски
- 7. Граф является k-хроматическим, если существует такое разбиение множества его вершин на k непересекающихся классов , что
- 8. Алгоритм раскраски вершин графа тогда сводится к следующему. Каким-либо методом находятся все максимальные пустые под-графы (например,
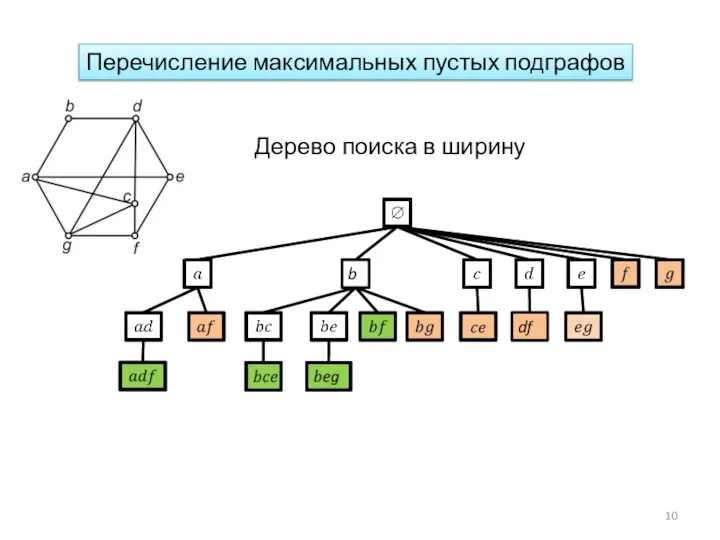
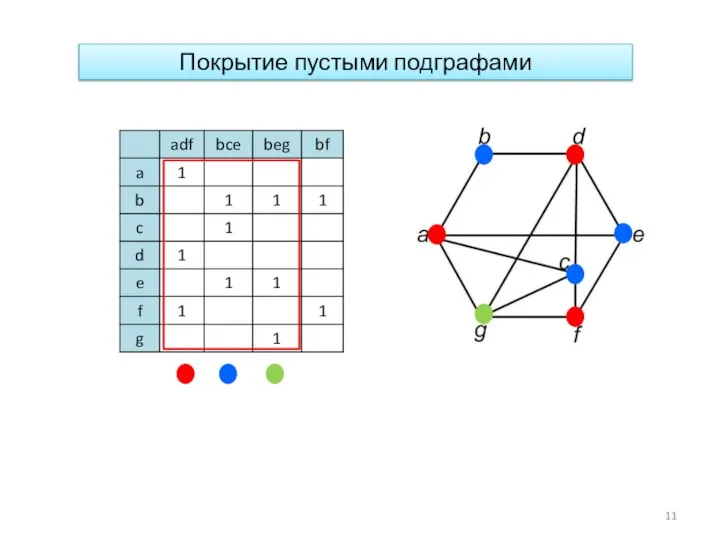
- 9. Этап 1. Выявление всех максимальных пустых подграфов Этап 2. Нахождение наименьшего покрытия вершин максимальными пустыми подграфами
- 10. b df Перечисление максимальных пустых подграфов Дерево поиска в ширину
- 11. Покрытие пустыми подграфами
- 12. 7.3. Приближенный алгоритм
- 13. Во многих приложениях размерность графа является довольно большой (сотни и тысячи вершин), однако нет жестких требований
- 14. Точный шаг: поглощение соцветных вершин Размерность раскрашиваемого графа можно уменьшить, если воспользоваться алгоритмом поиска и поглощения
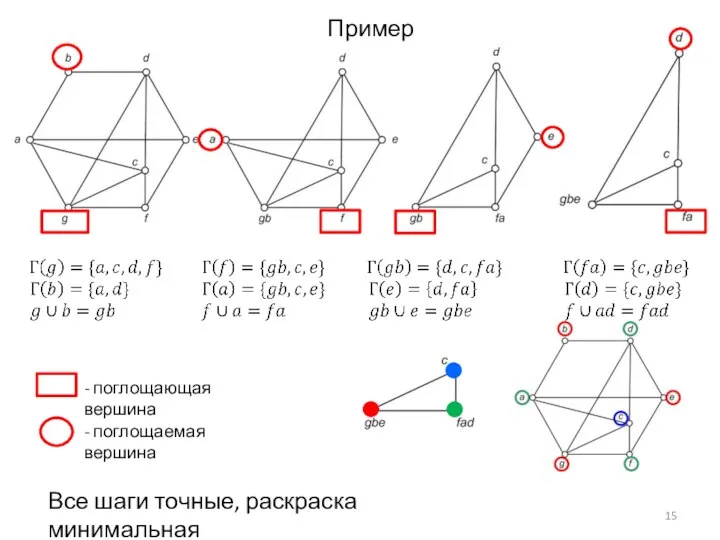
- 15. - поглощающая вершина - поглощаемая вершина Пример Все шаги точные, раскраска минимальная
- 16. Эвристический шаг: стягивание вершин Описанный выше шаг поглощения соцветных вершин является оптимальным с точки зрения раскраски,
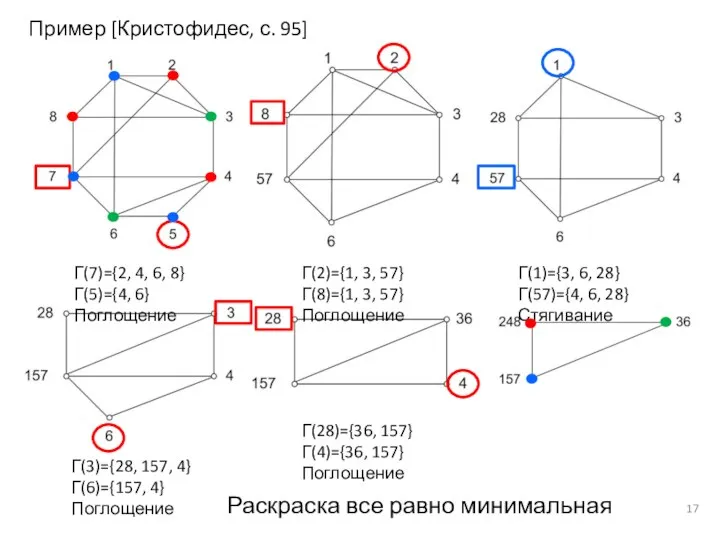
- 17. Г(7)={2, 4, 6, 8} Г(5)={4, 6} Поглощение Г(2)={1, 3, 57} Г(8)={1, 3, 57} Поглощение Г(1)={3, 6,
- 18. 7.4. Раскраска планарных графов
- 19. Планарные (плоские) графы Хотя на чертеже ребра граф можно изобразить любыми линиями, существуют свойства, зависящие от
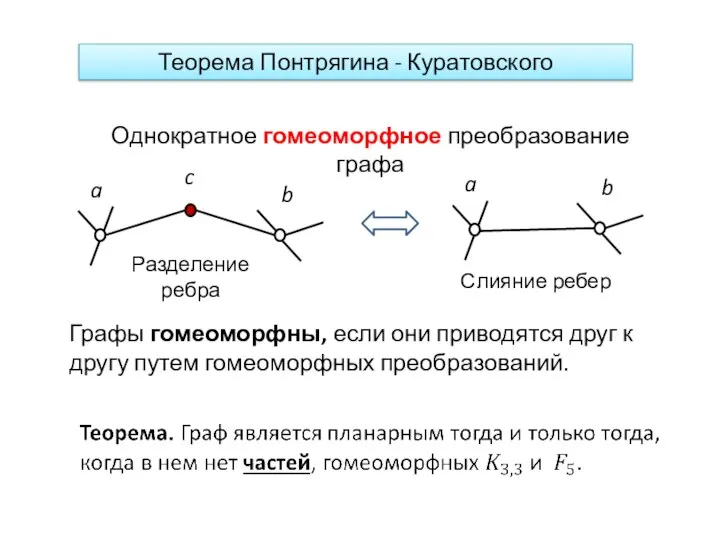
- 21. Теорема Понтрягина - Куратовского Однократное гомеоморфное преобразование графа Разделение ребра Графы гомеоморфны, если они приводятся друг
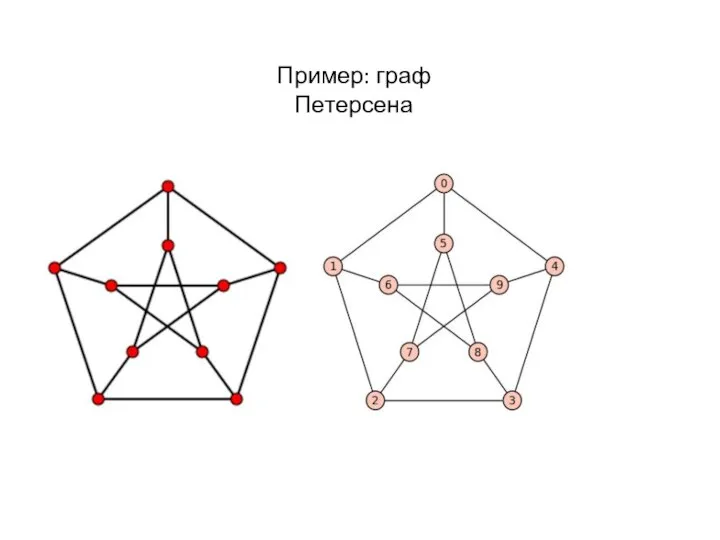
- 22. Пример: граф Петерсена
- 23. Понтрягин, Лев Семенович (1908-1988). Советский математик, один из крупнейших математиков 20 века. Академик АН СССР, Герой
- 24. Проблема четырех красок Теорема о четырёх красках утверждает, что всякую распо-ложенную на сфере карту можно раскрасить
- 29. Скачать презентацию



















 Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Подготовка к ЕГЭ, ГИА. Задачи на часы
Подготовка к ЕГЭ, ГИА. Задачи на часы Площади фигур в свете подготовки к ГИА - 9 класс
Площади фигур в свете подготовки к ГИА - 9 класс Презентация по математике "Состязание юных Матемптиков" - скачать
Презентация по математике "Состязание юных Матемптиков" - скачать  Линейная функция у=кх
Линейная функция у=кх Тела вращения. Использование ИКТ
Тела вращения. Использование ИКТ Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Умножение одночленов. Возведение одночлена в степень
Умножение одночленов. Возведение одночлена в степень Планиметрия и стереометрия
Планиметрия и стереометрия КвадратныйКорень_урок3-4!
КвадратныйКорень_урок3-4! Основы теории графов
Основы теории графов «….по одной капле воды… «….по одной капле воды… человек, умеющий мыслить логически, может сделать вывод о существовании Атлантического океана или Ниагарского водопада, даже если он не видел ни того, ни другого и никогда о них не слыхал… По ногтям
«….по одной капле воды… «….по одной капле воды… человек, умеющий мыслить логически, может сделать вывод о существовании Атлантического океана или Ниагарского водопада, даже если он не видел ни того, ни другого и никогда о них не слыхал… По ногтям Деление. Неправильные дроби
Деление. Неправильные дроби Поворот. (Геометрія. 9 клас)
Поворот. (Геометрія. 9 клас) Конкретный смысл умножения
Конкретный смысл умножения Современные ЦОР как условие эффективного обучения математике и информатике
Современные ЦОР как условие эффективного обучения математике и информатике В мире плоскостей
В мире плоскостей Высшая математика. Глава 1. Элементы линейной алгебры. Матрицы и определители
Высшая математика. Глава 1. Элементы линейной алгебры. Матрицы и определители Тригонометрический круг
Тригонометрический круг Основные понятия интеллектуальных систем. Знания. (Лекция 1)
Основные понятия интеллектуальных систем. Знания. (Лекция 1) Влияние математических действий на аликвоты
Влияние математических действий на аликвоты Сложение однозначных чисел с переходом через десяток
Сложение однозначных чисел с переходом через десяток Презентация по математике "Как построить симметричную фигуру" - скачать бесплатно
Презентация по математике "Как построить симметричную фигуру" - скачать бесплатно Геометрия. Решение задач
Геометрия. Решение задач Учитель математики Мацанова Ирина Александровна Олайнская средняя школа №2 г.Олайне Олайнский край, Латвия
Учитель математики Мацанова Ирина Александровна Олайнская средняя школа №2 г.Олайне Олайнский край, Латвия Первый признак подобия треугольников
Первый признак подобия треугольников Урок математики с элементами театрализации
Урок математики с элементами театрализации Вычисление площади фигур на клетчатой бумаге
Вычисление площади фигур на клетчатой бумаге