Содержание
- 2. Определение 1. Говорят, что задано отображение f: A → B, если заданы, во-первых, множество А (называемое
- 3. Упражнение 1. Петя сопоставил каждому городу России, где он бывал, число 1, каждому городу России, где
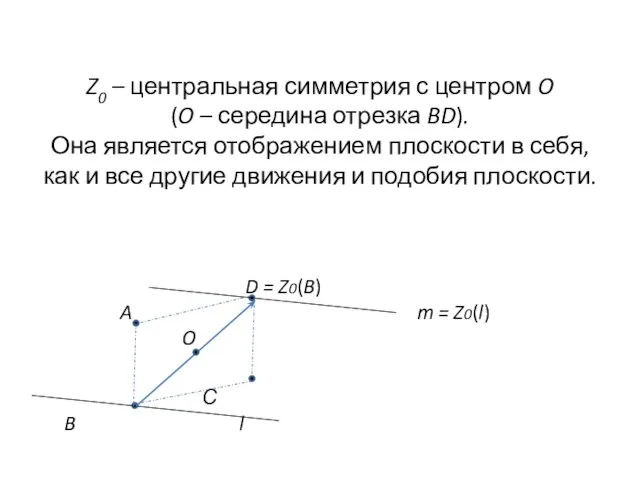
- 4. Упражнение 2 «Вершины A и C параллелограмма ABCD жестко закреплены, а вершина B пробегает прямую l.
- 5. Z0 – центральная симметрия с центром O (O – середина отрезка BD). Она является отображением плоскости
- 6. Упражнение 3 «a1 = 1, an+1 = an+1/n(n+1) при всех n ≥ 1. Чему равно a2018?»
- 7. Отображение, область определения которого --- множество всех натуральных чисел, называется последовательностью. У последовательностей аргумент по традиции
- 8. Упражнение 4 Задайте формулами последовательности: а) 2, 5, 8, 11, …; б) 2, 5, 10, 17,
- 9. Упражнение 5 Имеются три автомата. Первый прибавляет к любому введённому в него числу единицу, второй —
- 10. f(x) = x+1, g(y) = y2, h(z) = z-3. h(g(f(x))) = (x+1)2-3 Отображение из числового множества
- 11. Определение 2. Пусть заданы отображения f: A → B и g: B → C. Сопоставим каждому
- 12. Отображения из числовых множеств в числовые называют числовыми функциями. В упражнении 5 функции были заданы описаниями.
- 13. Тождественное отображение Последовательность г) из упражнения 4 — пример тождественного отображения, при котором каждый элемент переходит
- 14. Упражнение 7 Докажите, что все точки графика арифметической прогрессии an = a+nd (n = 0, 1,
- 15. Доказательство: Это график линейной функции y = dx+a. Как видим, графики у арифметической прогрессии и функции
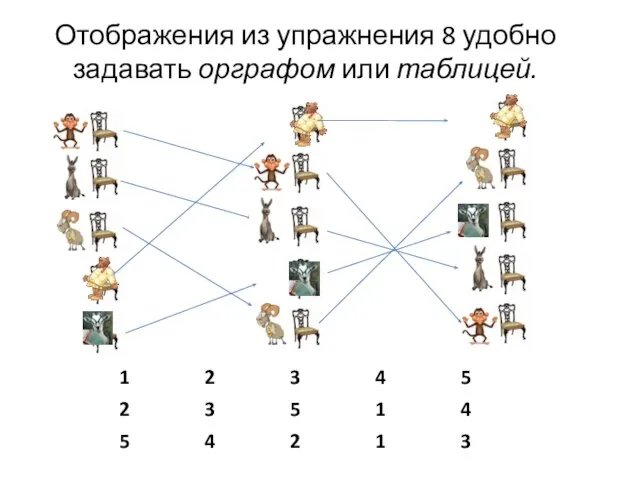
- 16. Упражнение 8 Проказница Мартышка, Осел, Козел и косолапый Мишка, а также Коза с баяном расселись, чтобы
- 17. Отображения из упражнения 8 удобно задавать орграфом или таблицей.
- 18. Определение 3 Если развернуть все стрелочки на их графах, задающих отображения в упражнении 8, то снова
- 19. Упражнение 9 Докажите следующие свойства обратных отображений: а) Если отображение f обратимо, то обратимо и отображение
- 20. Очевидно, отображение f: A → B обратимо тогда и только тогда, когда одновременно обладает двумя свойствами:
- 21. Определение 4 Отображение f: A → B называется инъективным/сюръективным, если в при этом отображении каждый элемент
- 22. Упражнение 10. Обратима ли композиция отображений h(g(f(x))) = (x+1)2-3 из упражнения 5?
- 23. Упражнение 11 Подберите в качестве областей определения и значений такие числовые множества, чтобы формула f(x) =
- 24. Упражнение 12 Многие комбинаторные задачи можно понимать как задачи о подсчёте тех или иных отображений. Так
- 26. Скачать презентацию





















 Сравнение, сложение и вычитание дробей с разными знаменателями. Урок-путешествие
Сравнение, сложение и вычитание дробей с разными знаменателями. Урок-путешествие Основные понятия теории вероятности
Основные понятия теории вероятности Тренажер. Счет в пределах 20. 1 класс
Тренажер. Счет в пределах 20. 1 класс Деление и дроби
Деление и дроби Решение задач на проценты. 5 класс. Урок № 5
Решение задач на проценты. 5 класс. Урок № 5 Сочетания
Сочетания Интерактивный тренажёр Реши уравнения
Интерактивный тренажёр Реши уравнения Аттестационная работа. Образовательная программа по внеурочной деятельности Наглядная геометрия
Аттестационная работа. Образовательная программа по внеурочной деятельности Наглядная геометрия Измерение площади и объёма
Измерение площади и объёма Элементы комбинаторики
Элементы комбинаторики Пересечение поверхностей
Пересечение поверхностей Готовимся к ГИА, 9 класс. Тест 4, часть 2
Готовимся к ГИА, 9 класс. Тест 4, часть 2 Обратные тригонометрические функции
Обратные тригонометрические функции Многоугольники, описанные около окружности. Геометрия, 8 класс
Многоугольники, описанные около окружности. Геометрия, 8 класс Уравнения. 5 класс
Уравнения. 5 класс Линейные ДУ n-го порядка
Линейные ДУ n-го порядка Теорема Виета. Алгебра 8 класс
Теорема Виета. Алгебра 8 класс Решение задач на основные теоремы теории вероятностей и на формулу полной вероятности
Решение задач на основные теоремы теории вероятностей и на формулу полной вероятности Деление на двузначное число. Решение задач (4 класс)
Деление на двузначное число. Решение задач (4 класс) Презентация на тему Вектор
Презентация на тему Вектор Показательные уравнения
Показательные уравнения Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Разведочный анализ данных. Цель и задачи. Обнаружение аномальных наблюдений. Критерий проверки
Разведочный анализ данных. Цель и задачи. Обнаружение аномальных наблюдений. Критерий проверки Квадрат
Квадрат Свойства чисел
Свойства чисел Симметрия относительно точки
Симметрия относительно точки Степень с натуральным показателем и ее свойства. Обобщение. 7 класс
Степень с натуральным показателем и ее свойства. Обобщение. 7 класс Двуполостный гиперболоид
Двуполостный гиперболоид