Содержание
- 2. План. Поняття функції. Способи задання. Загальні властивості функцій: 2.1. Область визначення. 2.2. Область значень. 2.3. Парність.
- 3. Означення функції Функція – це залежність змінної у від змінної х, при якій кожному значенню х
- 4. Функцію позначають: латинськими буквами f, g, h... (або f(х), g(х), h(х)...) рівностями у = f(х), у
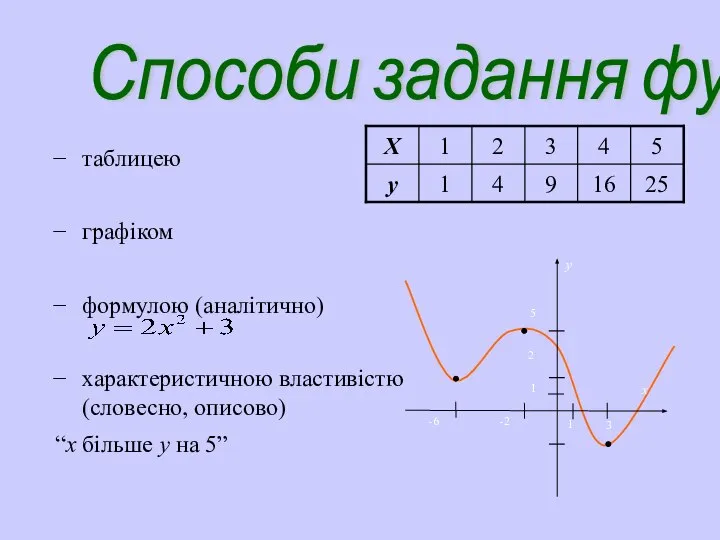
- 5. Способи задання функції таблицею графіком формулою (аналітично) характеристичною властивістю (словесно, описово) “х більше у на 5”
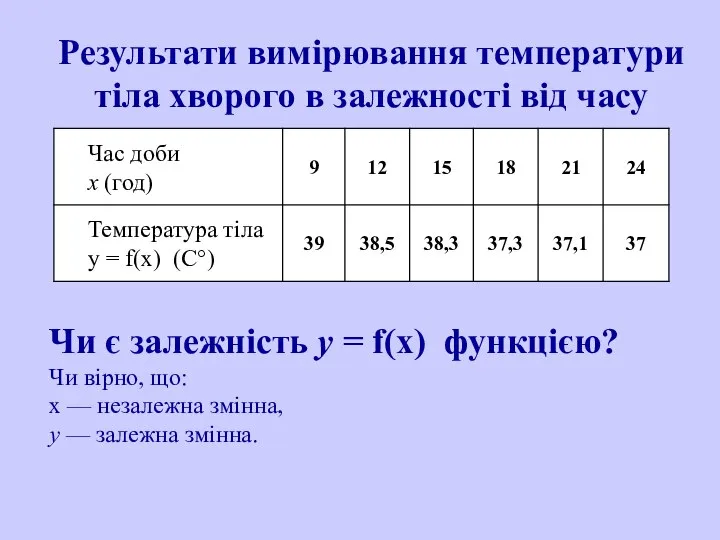
- 6. Результати вимірювання температури тіла хворого в залежності від часу Чи є залежність у = f(х) функцією?
- 7. Графіком функції у = f(х) називається множина всіх точок площини з координатами (х;f(х)), де перша координата
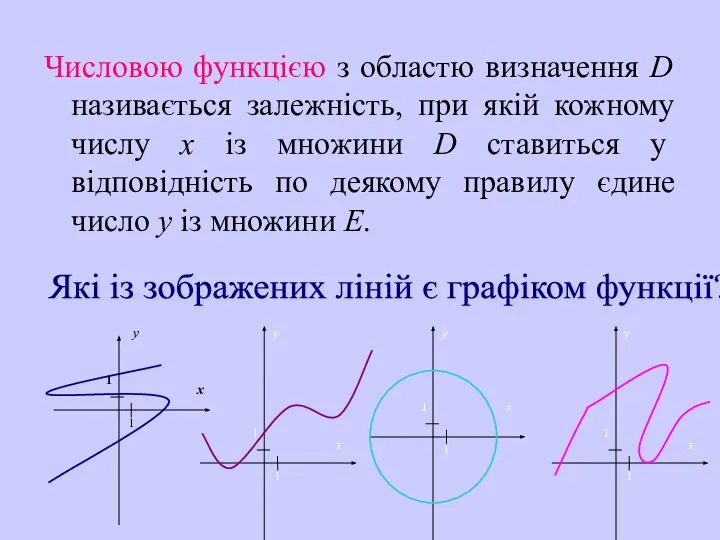
- 8. Числовою функцією з областю визначення D називається залежність, при якій кожному числу х із множини D
- 9. Існує декілька основних видів функцій: лінійна функція; пряма пропорційність; звернена пропорційність; квадратична функція; кубічна функція; функція
- 10. Область визначення функції у = f(х), яка задана формулою, називається множина тих значень, які може приймати
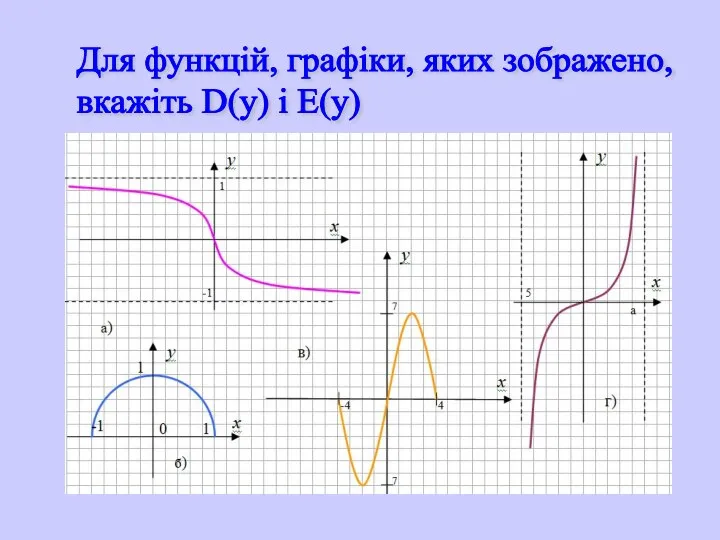
- 11. Для функцій, графіки, яких зображено, вкажіть D(y) і E(y)
- 12. 1) Якщо f(x) = P(x), де Р(х)- многочлен, ціла раціональна функція, то D (у) = (-∞;
- 13. Приклад. Знайти область визначення функції 1) f (х) = 2х + 3 D(f)=R або D(f) =
- 14. Для наступних функцій знайдіть D( f )
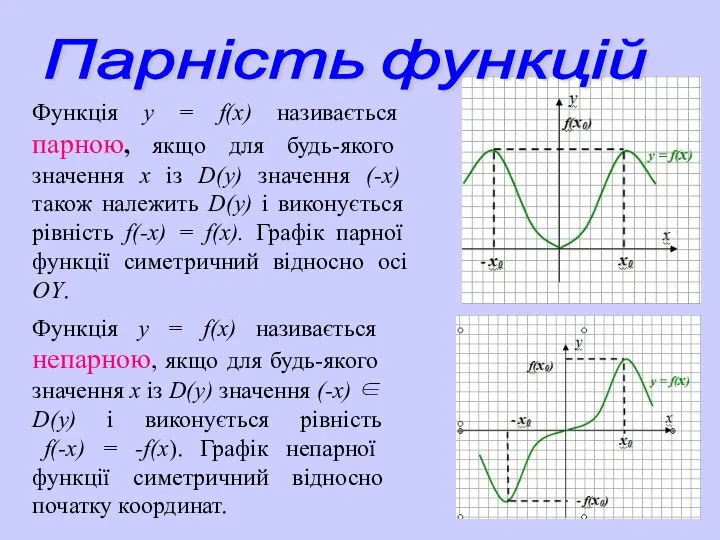
- 15. Функція у = f(х) називається парною, якщо для будь-якого значення х із D(у) значення (-х) також
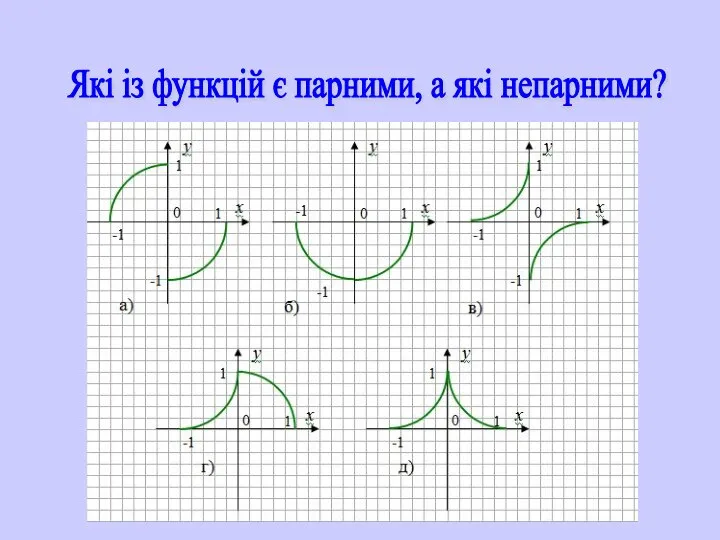
- 16. Які із функцій є парними, а які непарними?
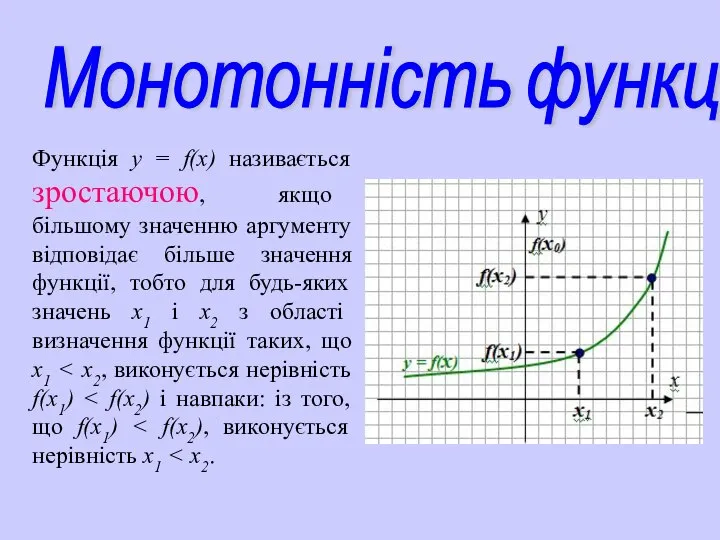
- 17. Функція у = f(х) називається зростаючою, якщо більшому значенню аргументу відповідає більше значення функції, тобто для
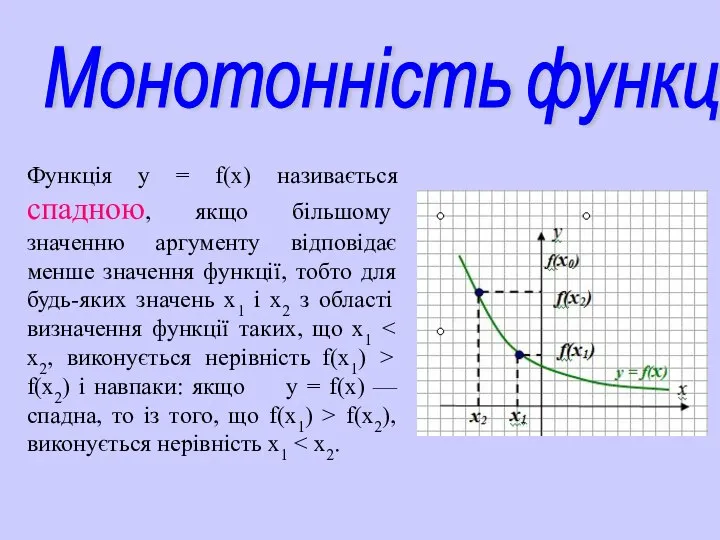
- 18. Монотонність функцій Функція у = f(х) називається спадною, якщо більшому значенню аргументу відповідає менше значення функції,
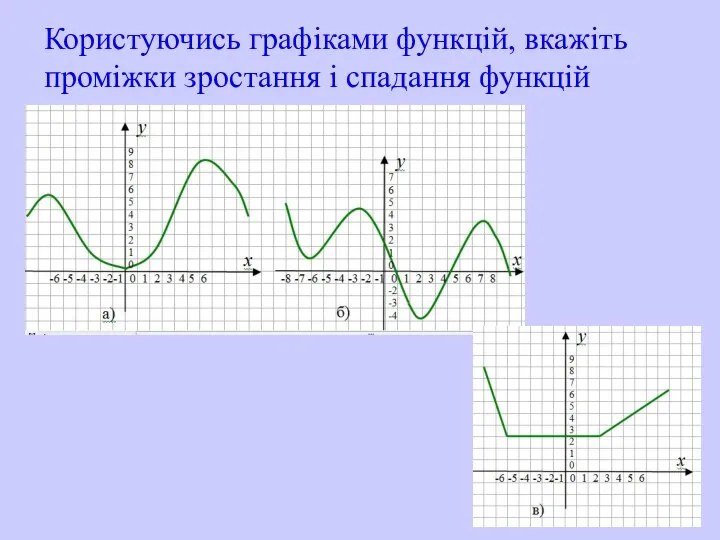
- 19. Користуючись графіками функцій, вкажіть проміжки зростання і спадання функцій
- 20. Взаємно обернені функції Дві функції f(х) та g(y) називаються взаємно оберененими, якщо формули у= f(х) та
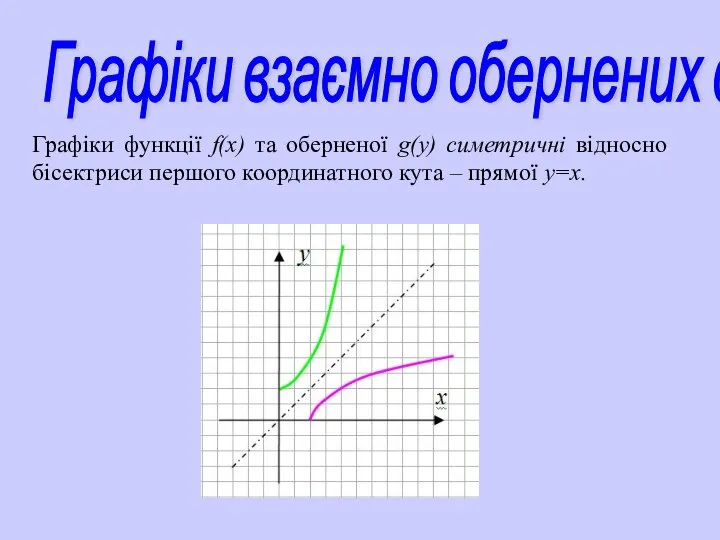
- 21. Графіки взаємно обернених функцій Графіки функції f(х) та оберненої g(y) симетричні відносно бісектриси першого координатного кута
- 22. Властивості взаємно обернених функцій Якщо f(х) та g(y) обернені функції, то область визначення функції f(х) співпадає
- 23. функция вида y = k х 1) D( f ) = R; 2) E( f )
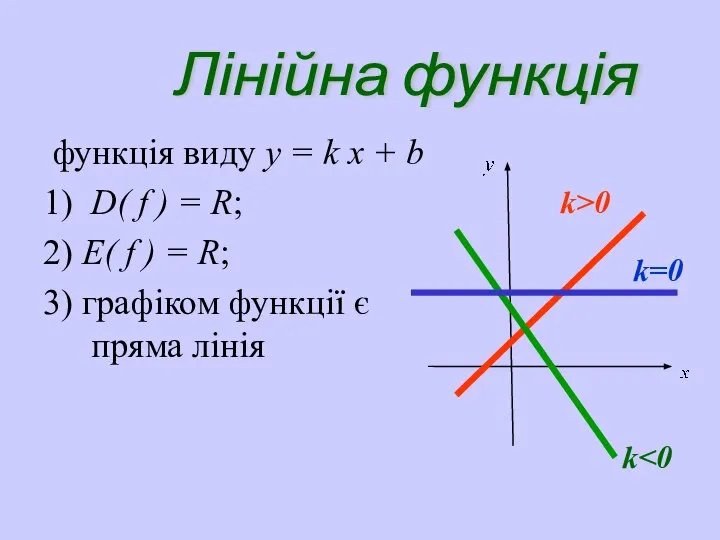
- 24. Лінійна функція функція виду y = k х + b 1) D( f ) = R;
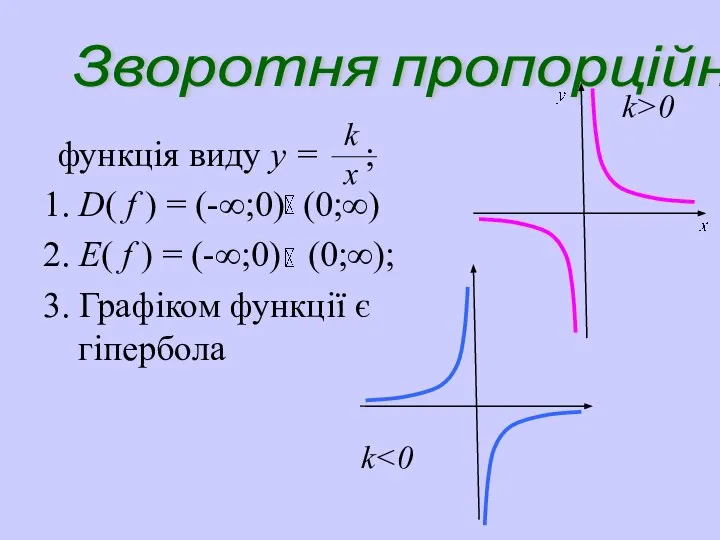
- 25. Зворотня пропорційність функція виду y = ; 1. D( f ) = (-∞;0) (0;∞) 2. E(
- 26. Квадратична функція функція виду y = x² ; D( f ) = R; 2. E( f
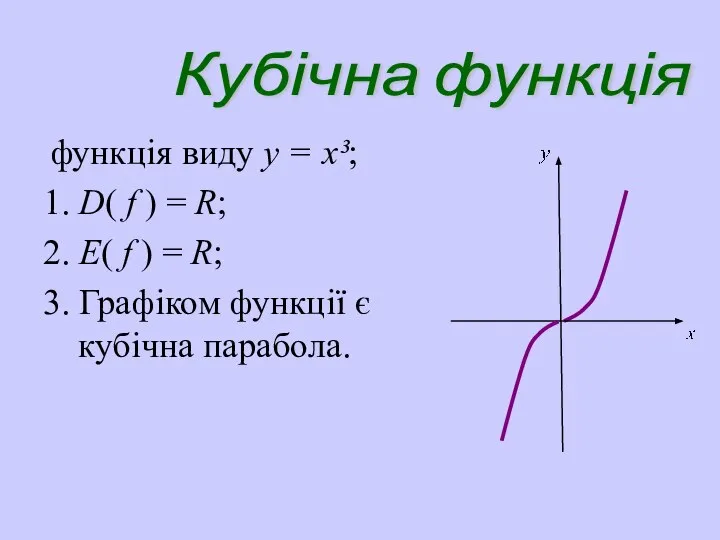
- 27. функція виду y = x³; 1. D( f ) = R; 2. E( f ) =
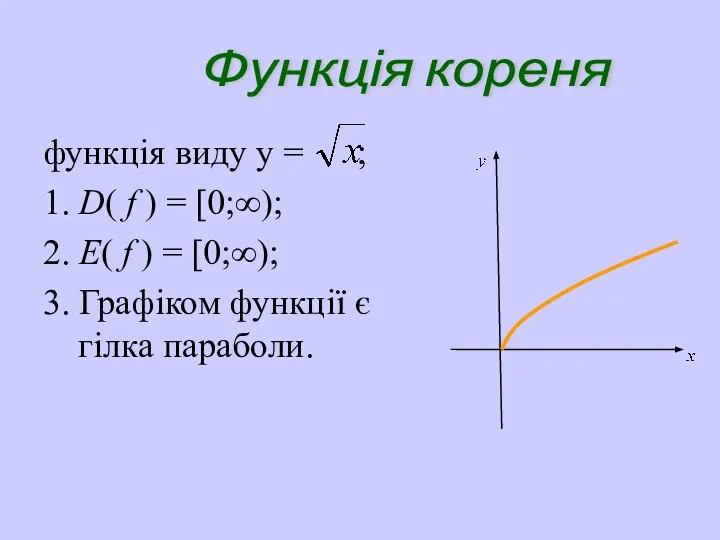
- 28. функція виду y = ; 1. D( f ) = [0;∞); 2. E( f ) =
- 29. функція виду y = |x|; 1. D( f ) = R; 2. E( f ) =
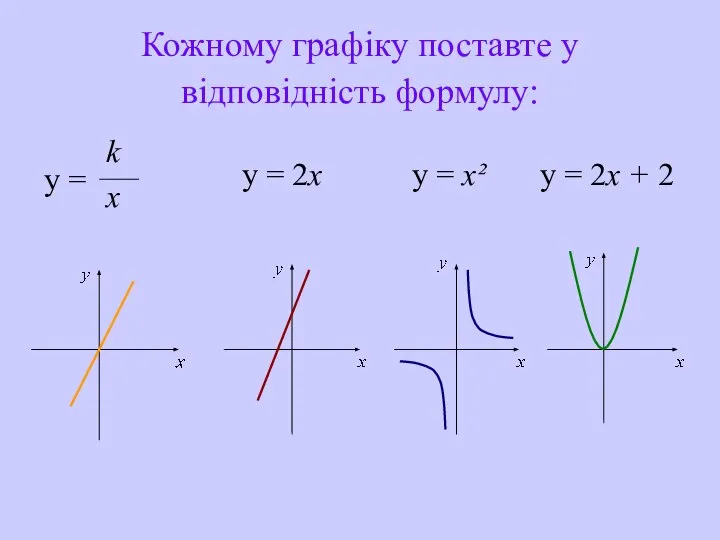
- 30. Кожному графіку поставте у відповідність формулу: y = k x y = x² y = 2x
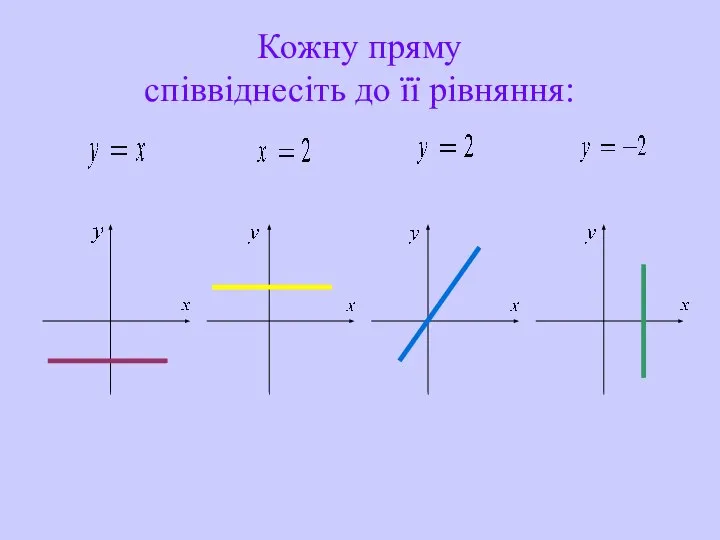
- 31. Кожну пряму співвіднесіть до її рівняння:
- 33. Скачать презентацию














 Проверка статистических гипотез
Проверка статистических гипотез Теория в области нечеткой логики и нечеткого множества
Теория в области нечеткой логики и нечеткого множества Формирование познавательного интереса школьников к учению на уроках математики
Формирование познавательного интереса школьников к учению на уроках математики Основы теории нечетких множеств
Основы теории нечетких множеств Рационал сандарды қорытындылау
Рационал сандарды қорытындылау Смежные и вертикальные углы. Задачи
Смежные и вертикальные углы. Задачи Деление с остатком
Деление с остатком Матрицы. Определители и их свойства (лекция № 1)
Матрицы. Определители и их свойства (лекция № 1) Активизация мыслительной деятельности учащихся на уроках математики
Активизация мыслительной деятельности учащихся на уроках математики Однородное уравнение повышенной сложности
Однородное уравнение повышенной сложности Квадратные уравнения. Повторение. 8 класс
Квадратные уравнения. Повторение. 8 класс История возникновения геометрии как науки
История возникновения геометрии как науки Решение задач с помощью уравнений. Устные вычисления
Решение задач с помощью уравнений. Устные вычисления Множества. Эквивалентные множества
Множества. Эквивалентные множества Презентация на тему Приведение дробей к общему знаменателю (урок в 6 классе)
Презентация на тему Приведение дробей к общему знаменателю (урок в 6 классе) Тригонометрические формулы. Диктант
Тригонометрические формулы. Диктант Параллельные прямые
Параллельные прямые Линии второго порядка
Линии второго порядка Математический аукцион (6 класс)
Математический аукцион (6 класс) Треугольник. Медиана, биссектриса, высота. Первый признак равенства треугольников
Треугольник. Медиана, биссектриса, высота. Первый признак равенства треугольников Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления
Сложение и вычитание многозначных чисел. Алгоритм письменного вычисления Решение рациональных уравнений
Решение рациональных уравнений Свойства квадарата
Свойства квадарата Презентация по математике "Путешествие в мир чисел" - скачать
Презентация по математике "Путешествие в мир чисел" - скачать  Фалес Милетский - один из первых геометров
Фалес Милетский - один из первых геометров "Веселый счет" (овощи)
"Веселый счет" (овощи) Численное решение обыкновенных дифференциальных уравнений
Численное решение обыкновенных дифференциальных уравнений Метод вспомогательной окружности
Метод вспомогательной окружности