Содержание
- 2. Если функции f(x) и g(x) непрерывны и дифференцируемы в окрестности точки x0 кроме, быть может, самой
- 3. Если дифференцируемая на интервале (a,b) функция y=f(x) возрастает (убывает), то для . Теорема Возрастание и убывание
- 4. Выпуклость функции Отрезком называется множество точек, удовлетворяющих равенству Определение
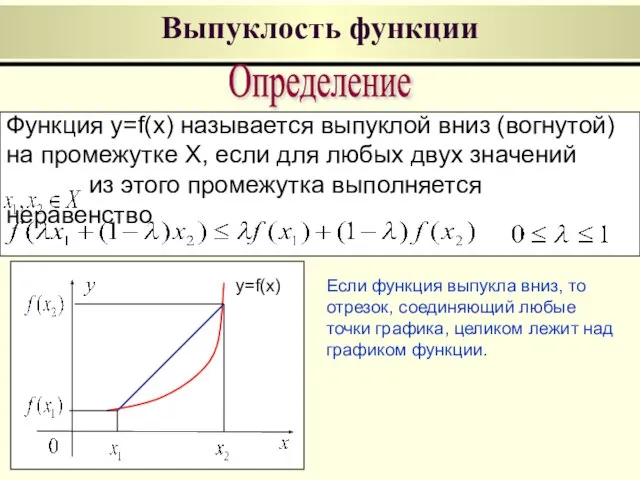
- 5. Выпуклость функции Функция y=f(x) называется выпуклой вниз (вогнутой) на промежутке X, если для любых двух значений
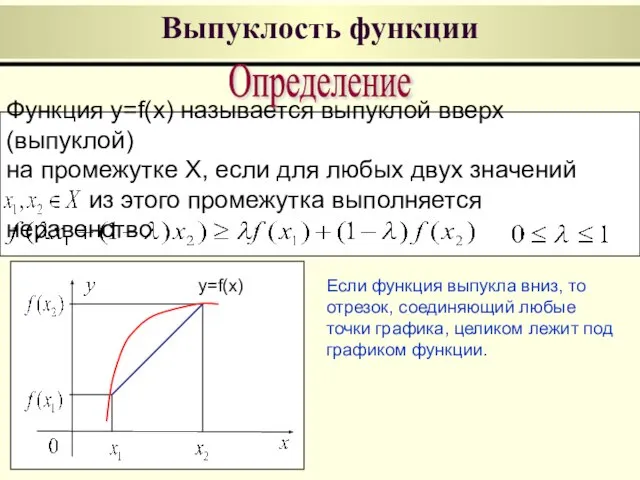
- 6. Выпуклость функции Функция y=f(x) называется выпуклой вверх (выпуклой) на промежутке X, если для любых двух значений
- 7. Если функция y=f(x) имеет то эта функция выпукла вниз(вверх) на интервале (a,b). Теорема Выпуклость функции (достаточное
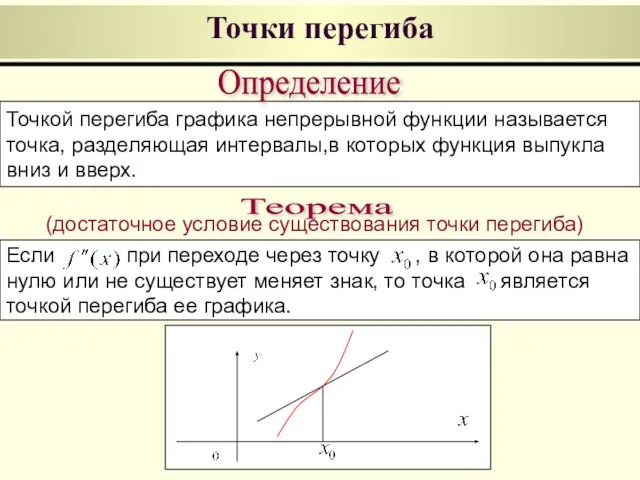
- 8. Точки перегиба Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы,в которых функция выпукла вниз и
- 9. Максимум и минимум функции Точка называется точкой максимума функции y=f(x), если Определение Точка называется точкой минимума
- 10. Для того, чтобы функция y=f(x) имела экстремум в точке необходимо, чтобы ее производная в этой точке
- 11. Если непрерывная функция y=f(x) дифференцируема в некоторой - окрестности критической точки и при переходе через нее
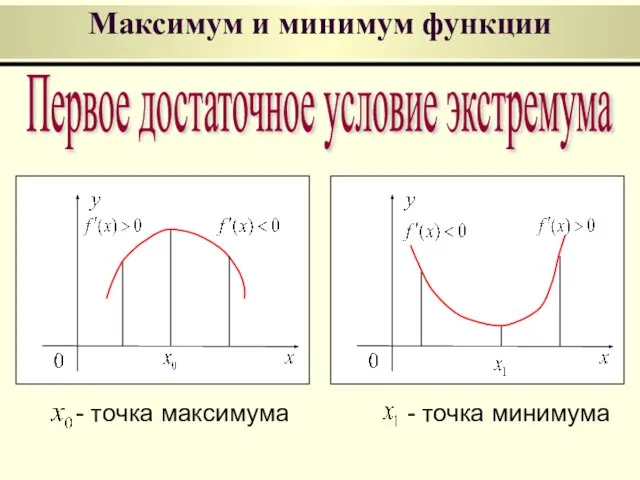
- 12. Первое достаточное условие экстремума Максимум и минимум функции - точка максимума - точка минимума
- 13. Выбрать те, которые являются внутренними точками области определения функции Максимум и минимум функции Найти критические точки
- 14. Найти экстремум функции не существуют при и + + - - точка максимума - максимум функции
- 15. Если в точке , а существует и , то если , то в точке функция имеет
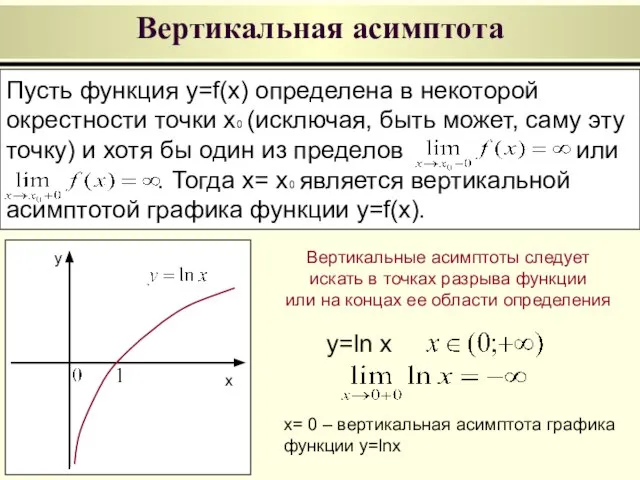
- 16. Вертикальная асимптота Пусть функция y=f(x) определена в некоторой окрестности точки x0 (исключая, быть может, саму эту
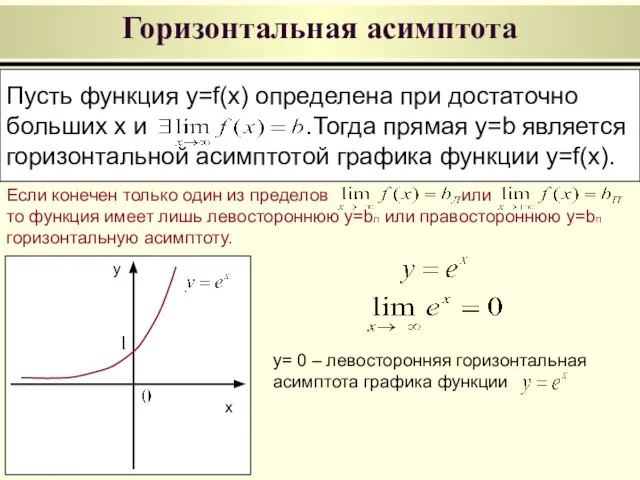
- 17. Горизонтальная асимптота Пусть функция y=f(x) определена при достаточно больших x и .Тогда прямая y=b является горизонтальной
- 18. Наклонная асимптота Пусть функция y=f(x) определена при достаточно больших x и существуют конечные пределы и .
- 19. Исследование на наличие асимптот y=0 – горизонтальная левосторонняя асимптота Так как , то вертикальных асимптот нет
- 20. Исследование на наличие асимптот x=1 – вертикальная асимптота при Так как и , то y=x+1 –
- 21. Найти (если возможно) точки пересечения графика с осями координат Общая схема исследования функции и построения графика
- 22. Исследовать функцию и построить ее график Точки пересечения с осями координат OX: y=0 - точки пересечения
- 23. Исследовать функцию и построить ее график Вертикальных асимптот нет, так как функция непрерывна - функция ни
- 24. Исследовать функцию и построить ее график при не существует при + + - - точка максимума
- 25. Исследовать функцию и построить ее график не существует при - точки перегиба + - -
- 27. Скачать презентацию


















 Решение уравнений, неравенств и их систем с модулями, 9 класс
Решение уравнений, неравенств и их систем с модулями, 9 класс Решение задач
Решение задач Решение уравнений (2 класс)
Решение уравнений (2 класс) Основы цифровой обработки сигналов (лекция 12)
Основы цифровой обработки сигналов (лекция 12) Inscribed and circumscribed circles of a triangle
Inscribed and circumscribed circles of a triangle Квадратные уравнения. Способы их решения. 8 класс
Квадратные уравнения. Способы их решения. 8 класс Теорема Пифагора. Урок 23
Теорема Пифагора. Урок 23 Решение задач на применение аксиом стереометрии и их следствий. Урок 3
Решение задач на применение аксиом стереометрии и их следствий. Урок 3 Методы математической обработки результатов исследования
Методы математической обработки результатов исследования Арифметический квадратный корень. Свойства квадратного корня Автор: ученик 8-а класса Гимназии №1 Сычев Алексей. Руководитель: Ил
Арифметический квадратный корень. Свойства квадратного корня Автор: ученик 8-а класса Гимназии №1 Сычев Алексей. Руководитель: Ил Основы сетевого планирования и управления (СПУ) разработками
Основы сетевого планирования и управления (СПУ) разработками урок Простейшие задачи в координатах
урок Простейшие задачи в координатах Площадь и периметр прямоугольника
Площадь и периметр прямоугольника Куля та сфера. (11 клас)
Куля та сфера. (11 клас) Счастливый случай Урок – семинар “Функции и их графики” 9 класс
Счастливый случай Урок – семинар “Функции и их графики” 9 класс Математическая карусель (начальная школа)
Математическая карусель (начальная школа) Угол. Прямой и развернутый угол. Чертежный треугольник. Транспортир
Угол. Прямой и развернутый угол. Чертежный треугольник. Транспортир Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Признаки делимости. Мультимедийный комбинированный урок. 5 класс
Признаки делимости. Мультимедийный комбинированный урок. 5 класс Письменное умножение на числа, оканчивающиеся нулями
Письменное умножение на числа, оканчивающиеся нулями Сравнение чисел. 6 класс
Сравнение чисел. 6 класс Логические функции
Логические функции Площадь трапеции
Площадь трапеции Балака Інна Петрівна Вчитель математики Кваліфікаційна категорія - спеціаліст 2 категорії Кобринівський НВК
Балака Інна Петрівна Вчитель математики Кваліфікаційна категорія - спеціаліст 2 категорії Кобринівський НВК  Векторы. Скалярные величины
Векторы. Скалярные величины Замечательные числа
Замечательные числа Обобщающий урок по теме: «Синус, косинус, тангенс суммы и разности аргументов. Презентация выполнена для уроков по алгебре и на
Обобщающий урок по теме: «Синус, косинус, тангенс суммы и разности аргументов. Презентация выполнена для уроков по алгебре и на Теория графов: основные понятия и определения
Теория графов: основные понятия и определения