Содержание
- 2. Тема 7. Дискретные случайные процессы 7. Дискретные случайные процессы 7.1. О характеристиках случайных величин 7.2. О
- 3. Дискретные случайные процессы При решении задач предыдущих разделов предполагалось, что входы в системы являются детерминированными функциями,
- 4. 7.1. О характеристиках случайных величин Случайной называют величину, которая в результате испытания примет одно числовое значение,
- 5. О характеристиках случайных величин Сначала рассмотрим дискретные случайные величины. Дискретная случайная величина Х случайным образом может
- 6. О характеристиках случайных величин Таким образом закон распределения дискретной случайной величины – это соответствие между возможными
- 7. О характеристиках случайных величин Если закон распределения одной случайной величины не зависит от того, какие значения
- 8. О характеристиках случайных величин Для вычисления вероятности совместного появления заданной пары значений двух случайных величин из
- 9. О характеристиках случайных величин Моментом К-го порядка случайной величины называется среднее значение Хk: Момент первого порядка
- 10. О характеристиках случайных величин Дисперсия характеризует размах – амплитуду отклонения случайной величины от среднего значения (т.е.
- 11. О характеристиках случайных величин Непрерывная случайная величина может принимать случайным образом любое значение внутри заданного конечного
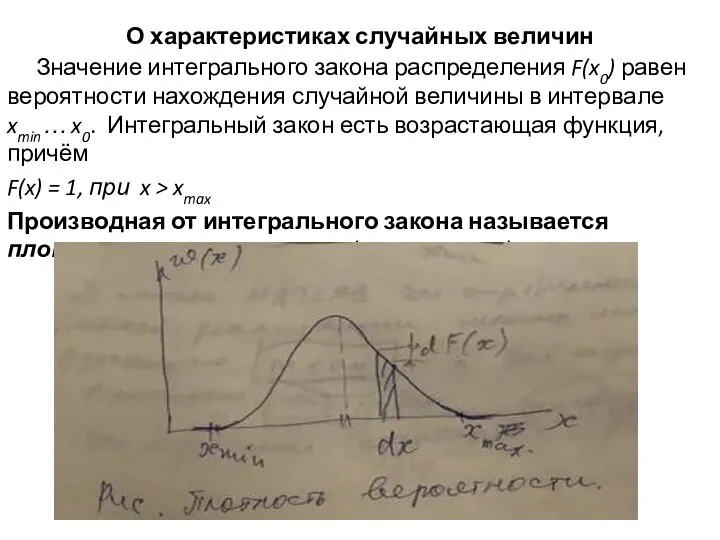
- 12. О характеристиках случайных величин Значение интегрального закона распределения F(x0) равен вероятности нахождения случайной величины в интервале
- 13. О характеристиках случайных величин Заштрихованная площадь на рис. выше равна вероятности попадания значений случайной величины на
- 14. О характеристиках случайных величин Для определения стандарта (т.е. среднеквадратичное отклонение ) – функцию std. Две непрерывные
- 15. О характеристиках случайных величин Если случайные величины независимы, априорные и условные плотности вероятности одинаковы, а плотность
- 16. О характеристиках случайных величин Если случайные величины независимы, то w(x|y) = w(x) w(y|x) = w(y) w(x,y)
- 17. О характеристиках случайных величин Действительно, в этом случае приведенное выше выражение для Rxy можно записать Случайные
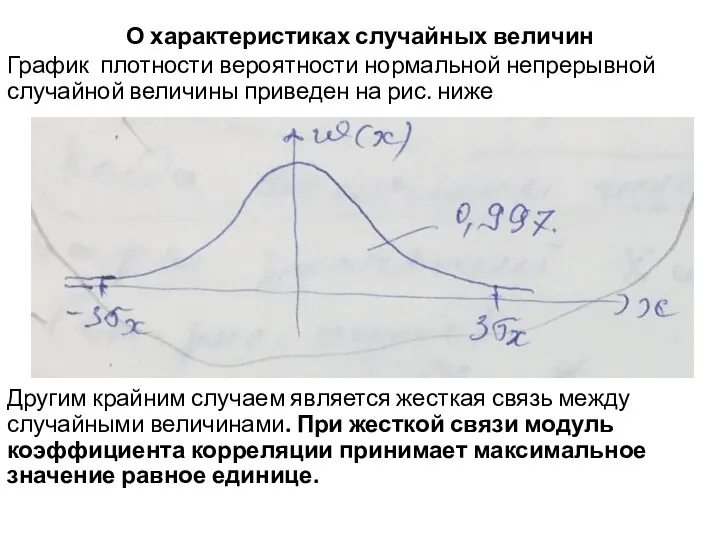
- 18. О характеристиках случайных величин График плотности вероятности нормальной непрерывной случайной величины приведен на рис. ниже Другим
- 19. О характеристиках случайных величин Рассмотрим выражение Матожидание неотрицательно, т.к. осредняется неотрицательная величина. Преобразуем Положив rxy =
- 20. Тогда из приведенных выше двух выражений следует, что: во- первых, матожидание равно нулю, поскольку матожидание берётся
- 21. Следовательно, рассмотрены крайние случаи. Когда величины жёстко связна (rxy = 1), пары значений x и y
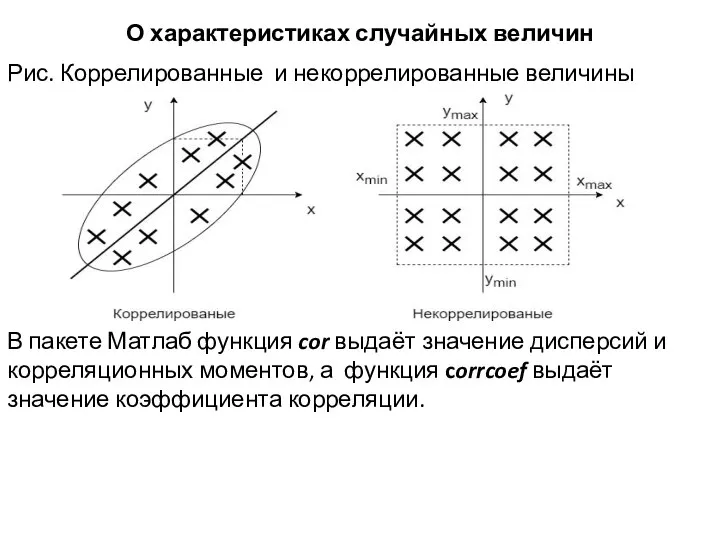
- 22. О характеристиках случайных величин Рис. Коррелированные и некоррелированные величины В пакете Матлаб функция cor выдаёт значение
- 23. 7.2. О характеристиках случайных процессов Случайные процессы являются частными случаями случайных функций. Случайные функции меняют своё
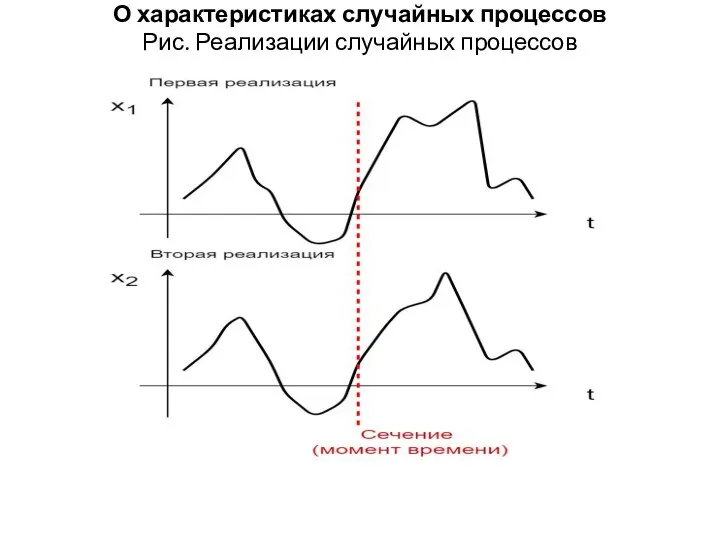
- 24. О характеристиках случайных процессов Рис. Реализации случайных процессов (
- 25. О характеристиках случайных процессов (на рис. выше внести изменения: обозначения осей ординат заменить x1 на x1(t),
- 26. О характеристиках случайных процессов Второй способ описания случайных процессов заключается в определении обычных и центрированных моментов.
- 27. О характеристиках случайных процессов Описание случайного процесса с помощью моментов не упрощает задачу, т.к. требует бесконечное
- 28. О характеристиках случайных процессов Случайные процессы называются нормальными, если закон распределения совокупности любого числа n его
- 30. Скачать презентацию























 Единицы массы
Единицы массы Основное свойство дроби
Основное свойство дроби Практикум по теме «Решение планиметрических задач из банка заданий ОГЭ № 24-25»
Практикум по теме «Решение планиметрических задач из банка заданий ОГЭ № 24-25» Решение заданий ЕГЭ В6 (часть 2)
Решение заданий ЕГЭ В6 (часть 2) Взаимодействие начальной школы и детского сада как условие творческого развития личности.
Взаимодействие начальной школы и детского сада как условие творческого развития личности. Приближенные вычисления
Приближенные вычисления Площадь треугольника
Площадь треугольника Деление и умножение десятичной дроби (6 класс)
Деление и умножение десятичной дроби (6 класс) Графическое решение уравнений с двумя переменными
Графическое решение уравнений с двумя переменными Квадратный корень из степени
Квадратный корень из степени Числовые ряды. Признаки сходимости числовых рядов. Лекция 12
Числовые ряды. Признаки сходимости числовых рядов. Лекция 12 Свойства сложения. Формула и свойство
Свойства сложения. Формула и свойство Работа с текстом на уроках математики
Работа с текстом на уроках математики Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Семинар 36)
Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Семинар 36) Аттестационная работа. Проектная деятельность по математике в 5-х классах
Аттестационная работа. Проектная деятельность по математике в 5-х классах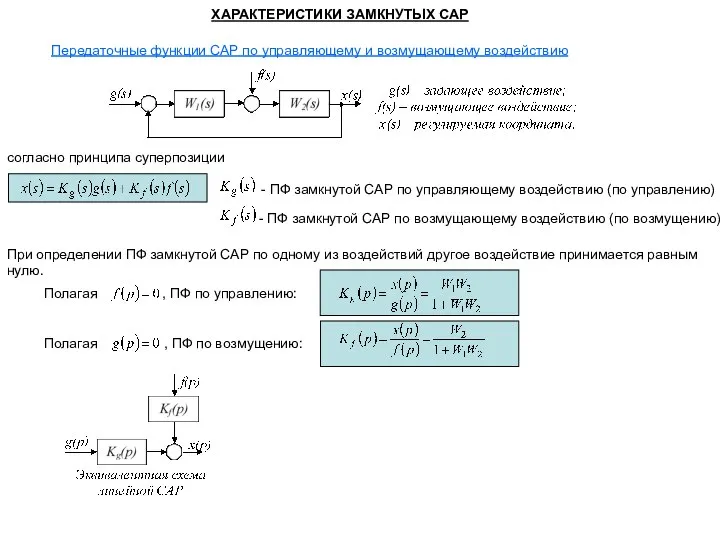 Характеристики замкнутых САР
Характеристики замкнутых САР Понятие о кривой распределения в психологии. (Лекция 3)
Понятие о кривой распределения в психологии. (Лекция 3) Исследовательская работа. Теорема Пифагора
Исследовательская работа. Теорема Пифагора Дробно-рациональные уравнения
Дробно-рациональные уравнения Квадраттық функция
Квадраттық функция Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения Нестандартные задачи по теме «Прогрессии» Цель урока: расширить и углубить знания по теме «Прогрессии»
Нестандартные задачи по теме «Прогрессии» Цель урока: расширить и углубить знания по теме «Прогрессии» Решение систем двух линейных уравнений с двумя неизвестными
Решение систем двух линейных уравнений с двумя неизвестными Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости Тригонометрические уравнения. Методы решения тригонометрических уравнений
Тригонометрические уравнения. Методы решения тригонометрических уравнений Статистика. Понятие, предмет и метод статистики. (Лекция 1)
Статистика. Понятие, предмет и метод статистики. (Лекция 1) Матриці та дії над ними. Поняття і види матриць
Матриці та дії над ними. Поняття і види матриць Пропорция. Решение задач с помощью пропорции
Пропорция. Решение задач с помощью пропорции