Содержание
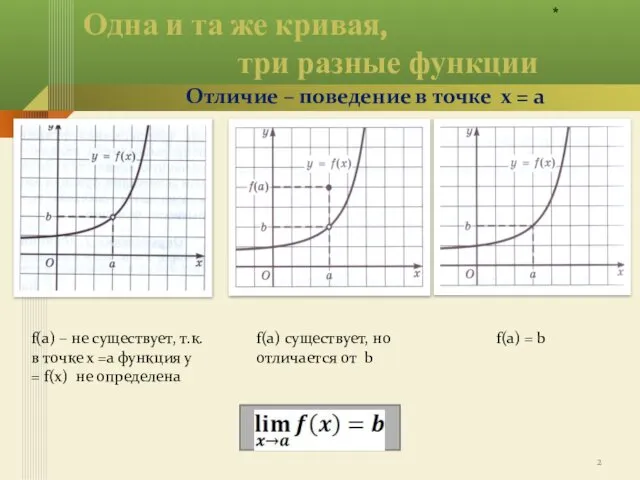
- 2. Одна и та же кривая, три разные функции Отличие – поведение в точке х = а
- 3. Какую из трех функций естественно считать непрерывной? Определение. Функцию у = f(х) называют непрерывной в точке
- 4. Если , , то Предел суммы равен сумме пределов. + = b+c ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИИ 2.
- 5. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
- 6. Вычисление пределов Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов: Эти
- 7. Примеры вычисления пределов *
- 8. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель
- 9. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить
- 10. Раскрытие неопределенностей Раскрытие неопределенности Умножим и разделим функцию на сопряженное выражение.
- 11. Первый замечательный предел
- 12. Выполнить задания В классе: №39.23(а,б)- №39.25(а,б); № 39.29(а,б) Дома: №39.23(в,г); № 39.27(в,г); №39.29(в) *
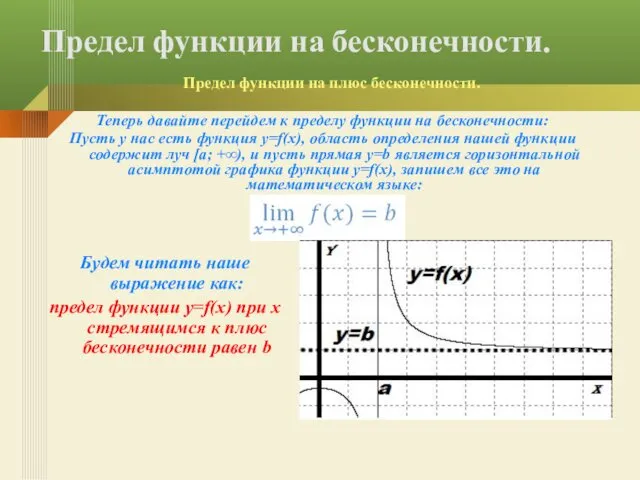
- 13. Теперь давайте перейдем к пределу функции на бесконечности: Пусть у нас есть функция y=f(x), область определения
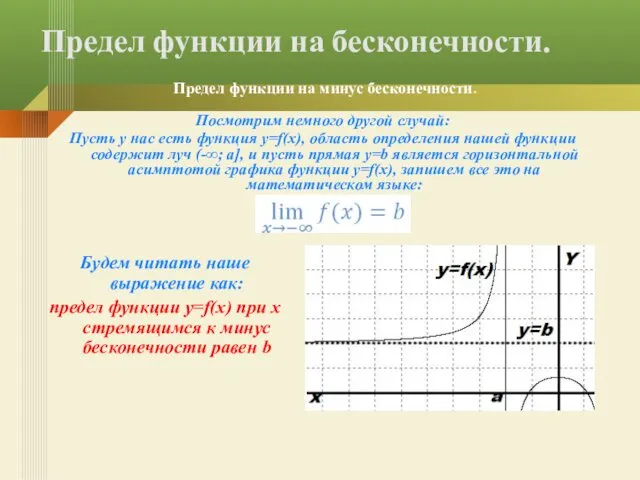
- 14. Посмотрим немного другой случай: Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч
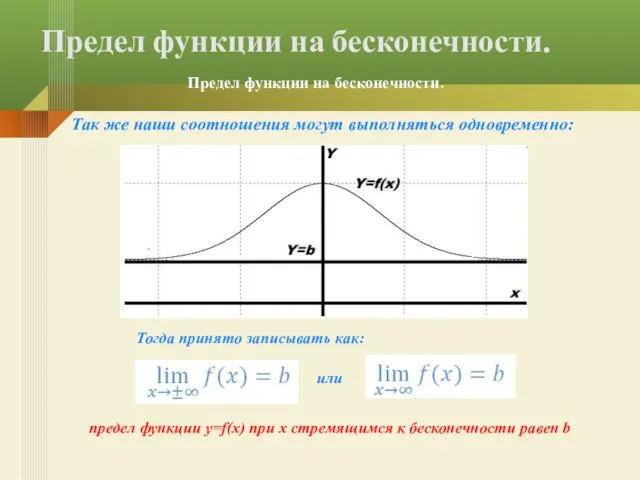
- 15. Так же наши соотношения могут выполняться одновременно: Предел функции на бесконечности. Предел функции на бесконечности. Тогда
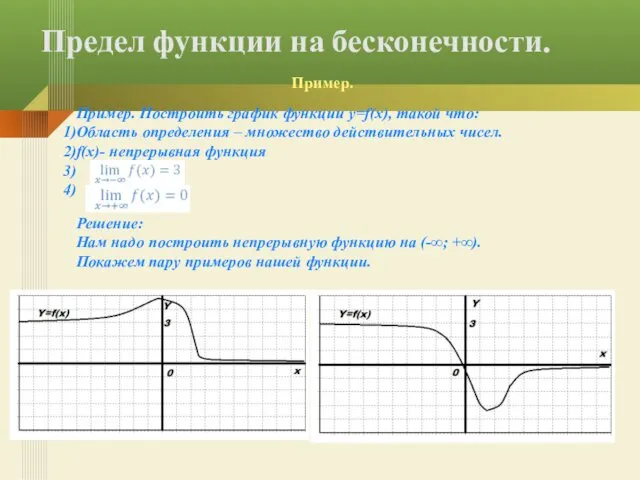
- 16. Предел функции на бесконечности. Пример. Пример. Построить график функции y=f(x), такой что: Область определения – множество
- 17. Предел функции на бесконечности. Для вычисления предела на бесконечности пользуются несколькими утверждениями: 1) Для любого натурально
- 18. Предел функции на бесконечности. Пример. Найти Решение. Разделим числитель и знаменатель дроби на x. Воспользуемся свойством
- 19. Предел функции на бесконечности. Пример. Найти предел функции y=f(x), при x стремящимся к бесконечности. Решение. Разделим
- 20. Предел функции на бесконечности. Пример. Найти предел функции y=f(x), при x стремящимся к бесконечности. Решение. Разделим
- 21. Задачи для самостоятельного решения. Предел функции на бесконечности. Построить график непрерывной функции y=f(x). Такой что предел
- 23. Скачать презентацию















 Сложение чисел с разными знаками
Сложение чисел с разными знаками Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна
Яковлева Ксения ученица 11 класса МБОУ «СОШ№22» г. Анжеро-Судженск, Кемеровской области Научный руководитель: Лилия Геннадьевна Функциональная грамотность на уроках математики
Функциональная грамотность на уроках математики Начальные сведения по теории вероятностей
Начальные сведения по теории вероятностей Координаты вектора
Координаты вектора Презентация на тему Перестановка слагаемых
Презентация на тему Перестановка слагаемых Чертежи разверток поверхностей геометрических тел
Чертежи разверток поверхностей геометрических тел Ребусы по математике
Ребусы по математике Математика, 5 класс Автор - Логунова Л.В.
Математика, 5 класс Автор - Логунова Л.В.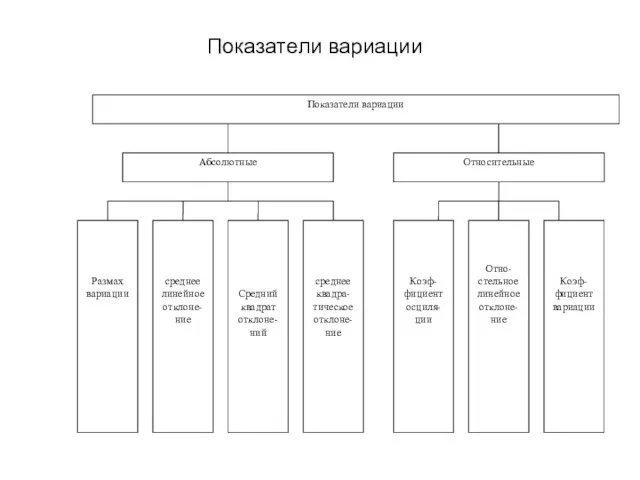 Показатели вариации
Показатели вариации пределы (1)
пределы (1) Эквивалентные отношения. Свойства эквивалентности
Эквивалентные отношения. Свойства эквивалентности Тренажер по графикам функций
Тренажер по графикам функций Случаи сложения и вычитания основанные на знаниях нумерации
Случаи сложения и вычитания основанные на знаниях нумерации Задачи на движение
Задачи на движение Начинаем мы опять решать, отгадывать, считать
Начинаем мы опять решать, отгадывать, считать Комбинаторика. Правило суммы
Комбинаторика. Правило суммы Построение таблиц истинности. Решение логических задач
Построение таблиц истинности. Решение логических задач Решение задач по математике
Решение задач по математике Solution methods for bilevel optimization
Solution methods for bilevel optimization Презентация к уроку алгебры Презентация к уроку алгебры в 10 классе по теме «Формулы суммы и разности синуса и косинуса.» Учит
Презентация к уроку алгебры Презентация к уроку алгебры в 10 классе по теме «Формулы суммы и разности синуса и косинуса.» Учит Умножение десятичной дроби на натуральное число
Умножение десятичной дроби на натуральное число Ломаные линии и многоугольники
Ломаные линии и многоугольники Устная работа (5m)2 (а4)3 57.63
Устная работа (5m)2 (а4)3 57.63  Выражения, тождества, уравнения
Выражения, тождества, уравнения Открытия Гаусса, Абеля и Галуа
Открытия Гаусса, Абеля и Галуа Презентация Учет инфляции в финансовых вычислениях
Презентация Учет инфляции в финансовых вычислениях Аттестационная работа. Исследовательская деятельность учащихся при построении доказательств по математике. (5-6 класс)
Аттестационная работа. Исследовательская деятельность учащихся при построении доказательств по математике. (5-6 класс)