Содержание
- 2. Основною задачею диференціального числення є задача диференціювання, тобто задача відшукання швидкості змінювання деякої функції. Але на
- 4. Нехай G(x) теж первісна для функції f (x) , тобто G′(x) = f (x) , але
- 5. Означення. Якщо F(x) первісна для функції f (x) , то вираз F(x) + C , де
- 6. З геометричної точки зору невизначений інтеграл - це сім’я кривих (інтегральних кривих), кожна з яких отримується
- 7. ТЕОРЕМА (про існування первісної). Якщо функція f (x) неперервна на деякому інтервалі, то для цієї функції
- 8. 1. Невизначений інтеграл від диференціала деякої функції дорівнює цій функції плюс довільна стала ∫dF(x) = F(x)
- 9. 3. ∫c ⋅ f (x) dx = c ⋅ ∫ f (x)dx , де c ≠
- 10. 3. ТАБЛИЦЯ НЕВИЗНАЧЕНИХ ІНТЕГРАЛІВ
- 11. 6. ∫cos xdx = sin x + C. 7. 8. 9.
- 13. Скачать презентацию










 Определители
Определители Знакомство детей с математическими знаками и монетами
Знакомство детей с математическими знаками и монетами Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств Расстояния в пространстве
Расстояния в пространстве Занимательная математика. Арифметика Л.Н.Толстого
Занимательная математика. Арифметика Л.Н.Толстого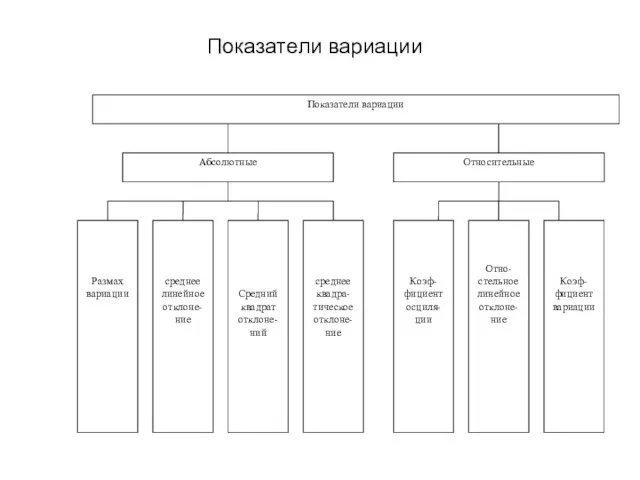 Показатели вариации
Показатели вариации Задачи на части. 5 класс
Задачи на части. 5 класс Векторы
Векторы Понятие логарифма. Определение логарифма
Понятие логарифма. Определение логарифма Рациональные числа. Математический диктант
Рациональные числа. Математический диктант Аналитическая геометрия
Аналитическая геометрия Поверхности второго порядка
Поверхности второго порядка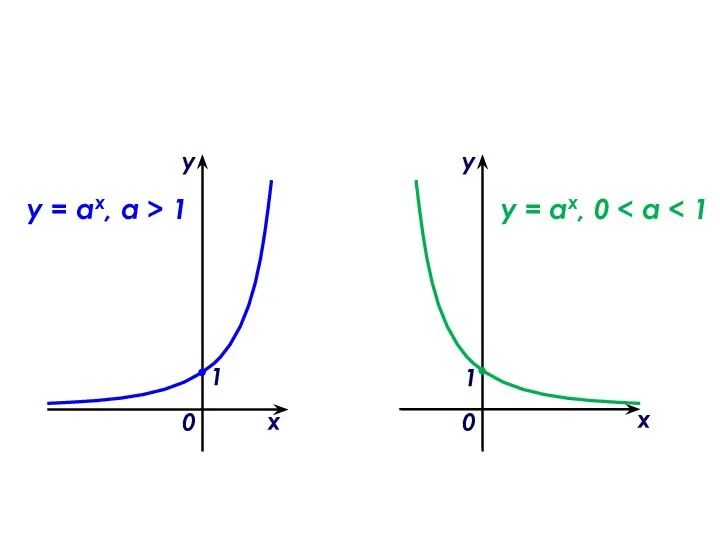 Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Деление и дроби
Деление и дроби Решение задач: «Первый признак подобия треугольников»
Решение задач: «Первый признак подобия треугольников»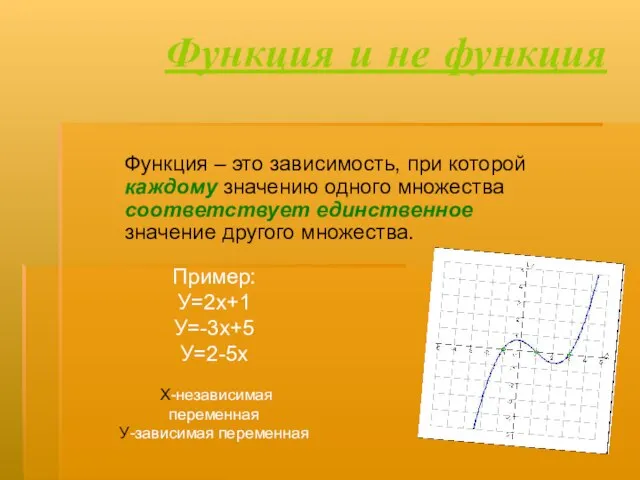 Функция и не функция Функция – это зависимость, при которой каждому значению одного множества соответствует единственное значен
Функция и не функция Функция – это зависимость, при которой каждому значению одного множества соответствует единственное значен Математика вокруг нас
Математика вокруг нас Комбинаторика и элементы теории вероятностей
Комбинаторика и элементы теории вероятностей Задания из открытого банка ЕГЭ
Задания из открытого банка ЕГЭ тренажер «Сложение в пределах 20»
тренажер «Сложение в пределах 20» Применение методов статистического анализа для изучения общественного здоровья
Применение методов статистического анализа для изучения общественного здоровья Свойство медиан треугольника
Свойство медиан треугольника Площадь треугольника
Площадь треугольника Работа в программе Excel на уроках математики. Составление таблиц и диаграмм, анализ статистических данных
Работа в программе Excel на уроках математики. Составление таблиц и диаграмм, анализ статистических данных Степень с натуральным показателем и его свойства (7 кл)
Степень с натуральным показателем и его свойства (7 кл) Электронное пособие для подготовки к ЕГЭ 2012 год. Подготовка к ЕГЭ
Электронное пособие для подготовки к ЕГЭ 2012 год. Подготовка к ЕГЭ Правильные многоугольники в нашей жизни
Правильные многоугольники в нашей жизни Упрощение выражений
Упрощение выражений