Содержание
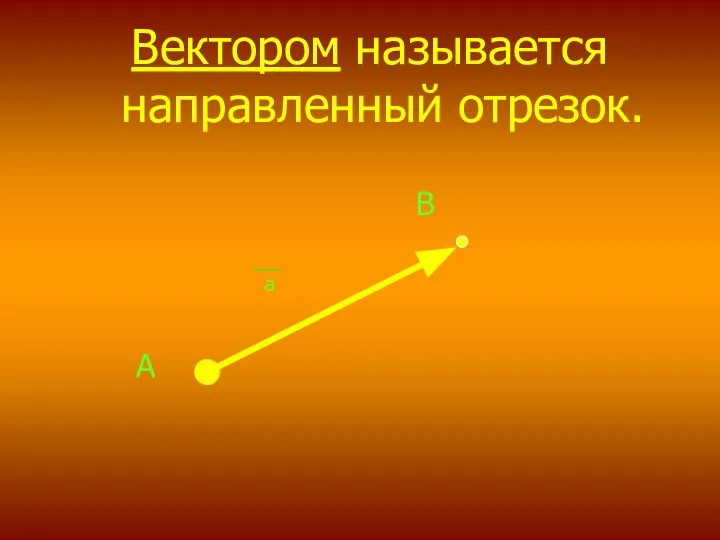
- 2. Вектором называется направленный отрезок. В а А
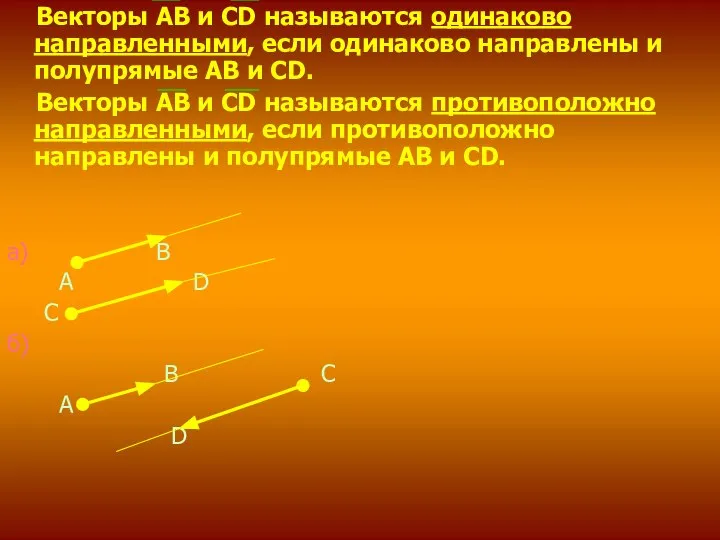
- 3. Векторы АВ и СD называются одинаково направленными, если одинаково направлены и полупрямые АВ и CD. Векторы
- 4. Абсолютной величиной (или модулем) вектора называется длина отрезка, задающего вектор. Абсолютная величина нуль – вектора равна
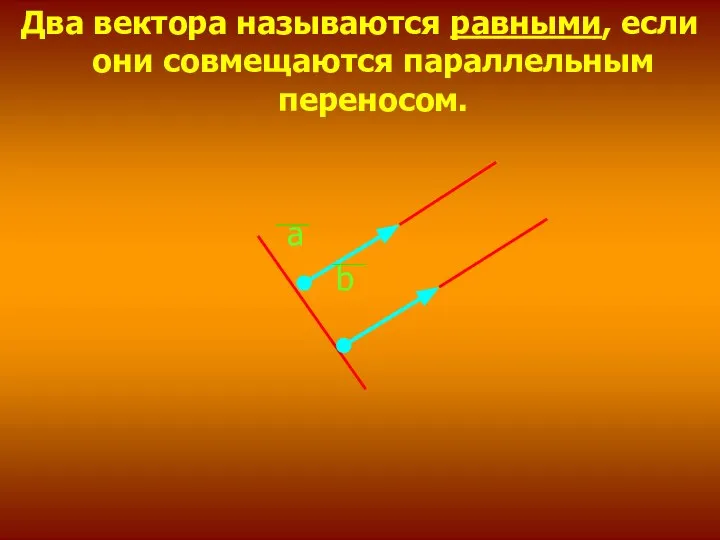
- 5. Два вектора называются равными, если они совмещаются параллельным переносом. а b
- 6. Равные векторы одинаково направлены и равны по абсолютной величине. И наоборот, если векторы одинаково направлены и
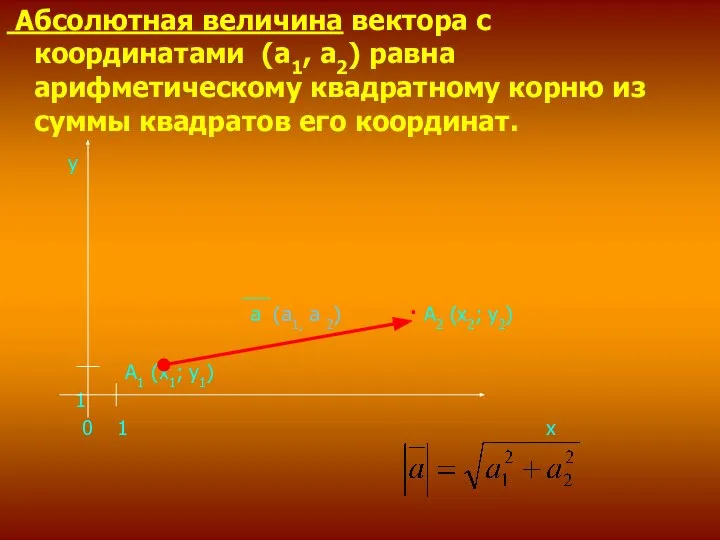
- 7. Пусть вектор а имеет началом точку А1(х1; у1), а концом – точку А2(х2; у2). Координатами вектора
- 8. Абсолютная величина вектора с координатами (а1, а2) равна арифметическому квадратному корню из суммы квадратов его координат.
- 9. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
- 10. Суммой векторов а и b с координатами (а1, а2 ) и (b1, b2) называется вектор с
- 11. ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ a + 0 = а a + b = b + a a
- 12. ПРАВИЛО ТРЕУГОЛЬНИКОВ Какими бы ни были точки А, В, С, подтверждается векторное равенство: АВ + ВС
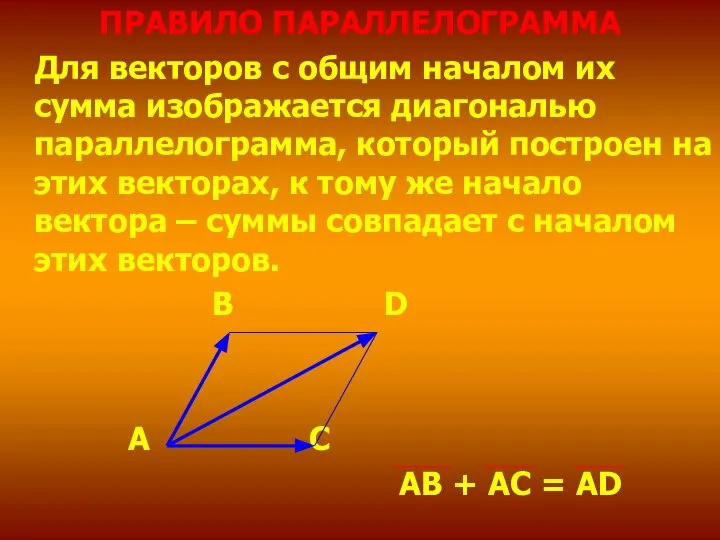
- 13. ПРАВИЛО ПАРАЛЛЕЛОГРАММА Для векторов с общим началом их сумма изображается диагональю параллелограмма, который построен на этих
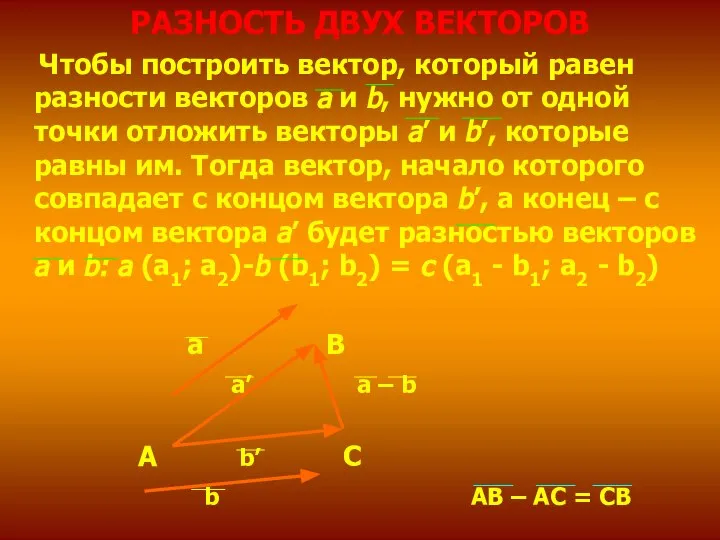
- 14. РАЗНОСТЬ ДВУХ ВЕКТОРОВ Чтобы построить вектор, который равен разности векторов а и b, нужно от одной
- 15. Произведением вектора (а1; а2) на число λ называется вектор (λа1; λа2), то есть (а1; а2)λ =
- 16. ЗАКОНЫ УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО Для любого вектора а и чисел λ, μ (λ + μ)а
- 17. СВОЙСТВА УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО Абсолютная величина вектора λа равна ⎢λ ⎢× ⎢а ⎢. Направление вектора
- 18. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. а) a
- 19. Если векторы коллинеарны, то их соответствующие координаты пропорциональны, и наоборот, если соответствующие координаты двух векторов пропорциональны,
- 20. РАЗЛОЖЕНИЕ ВЕКТОРА ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ Любой вектор с можно разложить по двум неколлинеарным векторам а
- 21. СКАЛЯРНЫМ ПРОИЗВЕДЕНИЕМ ВЕКТОРОВ a(a1; a2) и b(b1; b2) НАЗЫВАЕТСЯ ЧИСЛО a1b1 + a2b2.
- 22. СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 1. Скалярный квадрат вектора равен квадрату его абсолютной величины, a то есть
- 24. Скачать презентацию















 Методы интегрирования
Методы интегрирования Решение задач по теме «Параллелограмм»
Решение задач по теме «Параллелограмм» Многогранники. Гимнастика ума
Многогранники. Гимнастика ума Табличное сложение и вычитание
Табличное сложение и вычитание Решение задач Выполнила Хижняк Светлана Анатольевна Учитель МБОУ СОШ №9, город Златоуст, Челябинская область. 2010 год
Решение задач Выполнила Хижняк Светлана Анатольевна Учитель МБОУ СОШ №9, город Златоуст, Челябинская область. 2010 год  Геометрическая прогрессия
Геометрическая прогрессия Алгоритм нахождения наименьшего и наибольшего значений показательной функции
Алгоритм нахождения наименьшего и наибольшего значений показательной функции Циклический алгоритм на QBASIC. Вложенные циклы
Циклический алгоритм на QBASIC. Вложенные циклы Вычитание смешанных дробей
Вычитание смешанных дробей Производная функции
Производная функции Теорема Пифагора. Задачи
Теорема Пифагора. Задачи Элективный курс «Алгебра модуля»
Элективный курс «Алгебра модуля» Наибольший общий делитель. 5 класс
Наибольший общий делитель. 5 класс Сложение и вычитание дробей с разными знаменателями. 6 класс
Сложение и вычитание дробей с разными знаменателями. 6 класс Математичні софізми
Математичні софізми Представьте числа в виде суммы разрядных слагаемых
Представьте числа в виде суммы разрядных слагаемых Использование триангуляции при моделировании сложных объектов
Использование триангуляции при моделировании сложных объектов Интегральные исчисления
Интегральные исчисления Загадочный мир фракталов
Загадочный мир фракталов Функции нескольких переменных
Функции нескольких переменных Математики и математика в годы Великой Отечественной войны
Математики и математика в годы Великой Отечественной войны Алгебра логики
Алгебра логики Параллелограмм
Параллелограмм Сфера. Сфеерическая геометрия
Сфера. Сфеерическая геометрия Пирамида. Усеченная пирамида
Пирамида. Усеченная пирамида Коэффициенты линейной функции
Коэффициенты линейной функции Відомі математики
Відомі математики Параллельные прямые
Параллельные прямые