Содержание
- 2. Overview Basic Probability Discrete Random Variables Continuous Random Variables Concepts Laws and Notation Conditional Probability Total
- 3. BASIC PROBABILITY CONCEPTS: ‘Experiments’ and ‘Events’ Experiment: an action whose outcome is uncertain (roll a die)
- 4. How to measure probability Probability: measure of how likely an event is to occur (between 0
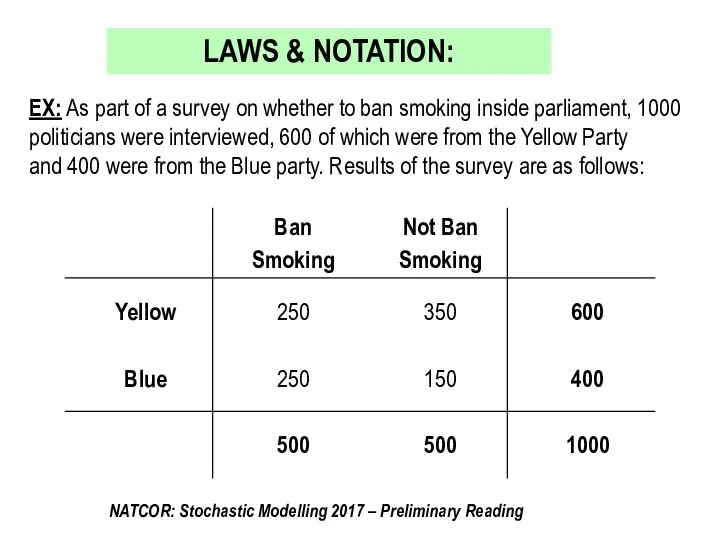
- 5. EX: As part of a survey on whether to ban smoking inside parliament, 1000 politicians were
- 6. Probability that a person chosen randomly (i.e. everyone has an equal chance of selection) from the
- 7. Probability that a person chosen randomly from the survey is a member of the Yellow Party
- 8. Probability that a person chosen is either from the Yellow Party ( Y ) or would
- 9. Addition Law for Probabilities (in general): A special case is when Events A and B are
- 10. The Conditional Probability that a randomly chosen person would ban smoking ( Ban ) given that
- 11. Multiplication Law for Probabilities (in general) or A special case is when Events A and B
- 12. Law of Total Probability EX: The results of the survey on whether to ban smoking inside
- 13. Law of Total Probability in general Suppose events A1, A2, A3, … An are mutually exclusive
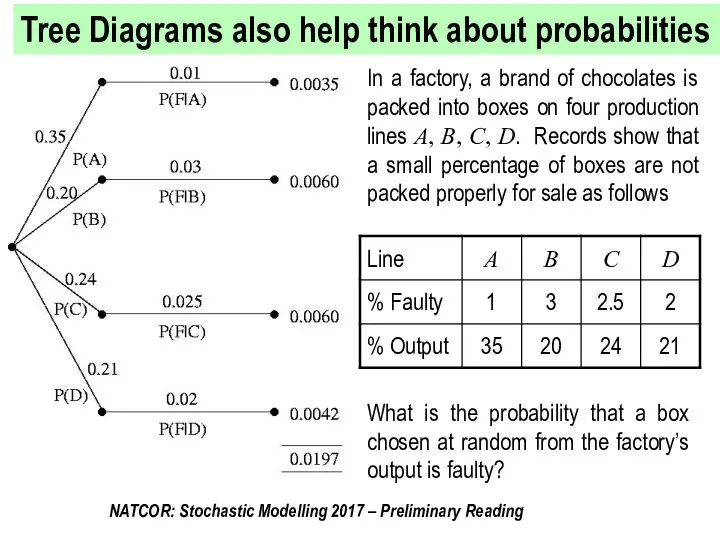
- 14. Tree Diagrams also help think about probabilities In a factory, a brand of chocolates is packed
- 15. Discrete Random Variables A random variable is a numerical description of the outcome of an experiment.
- 16. Probability Mass Function (pmf) of a discrete random variable The pmf, p(x), of a discrete random
- 17. Expected value and variance of discrete random variables The expected value, or mean, of a discrete
- 18. E.g. Sum of values when two dice are thrown:
- 19. Expected value and variance of combinations of discrete random variables If X and Y are random
- 20. Law of Total Probability for Expected Values of a discrete random variable Suppose events A1, A2,
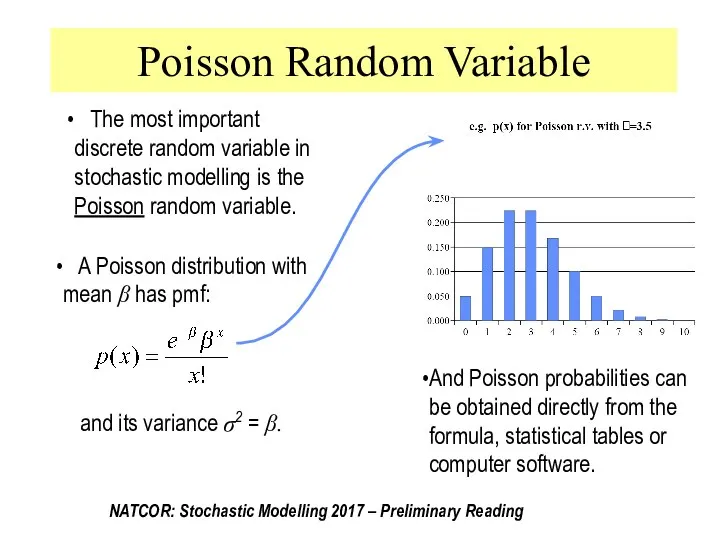
- 21. Poisson Random Variable The most important discrete random variable in stochastic modelling is the Poisson random
- 22. The General Theory: When ‘events’ of interest occur ‘at random’ at rate λ per unit time;
- 23. Example: If arrivals of customers to a bank are at random, at an average rate of
- 24. Continuous Random Variables A random variable is a numerical description of the outcome of an experiment.
- 25. Probability Density Functions (p.d.f.) The random behaviour of a continuous random variable X is captured by
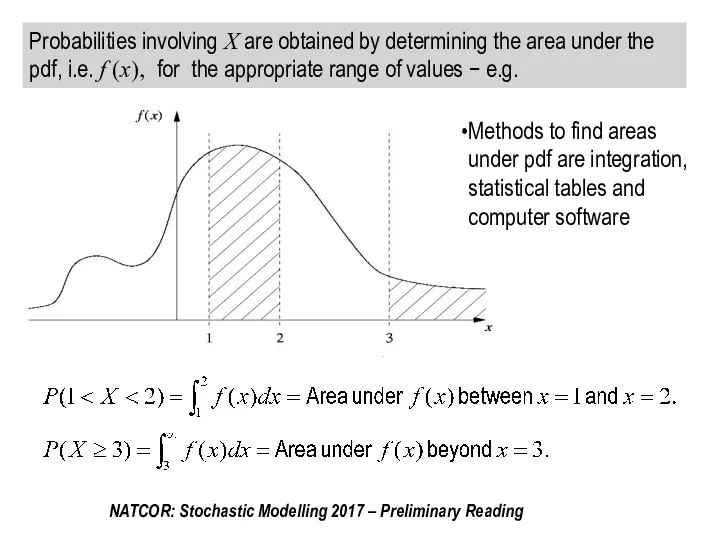
- 26. Probabilities involving X are obtained by determining the area under the pdf, i.e. f (x), for
- 27. Expected value and variance of continuous random variables The expected value, or mean, of a continuous
- 28. Expected value and variance of combinations of continuous random variables NB. Exactly same as for discrete
- 29. Law of Total Probability for Expected Values of a continuous random variable NB. Exactly same as
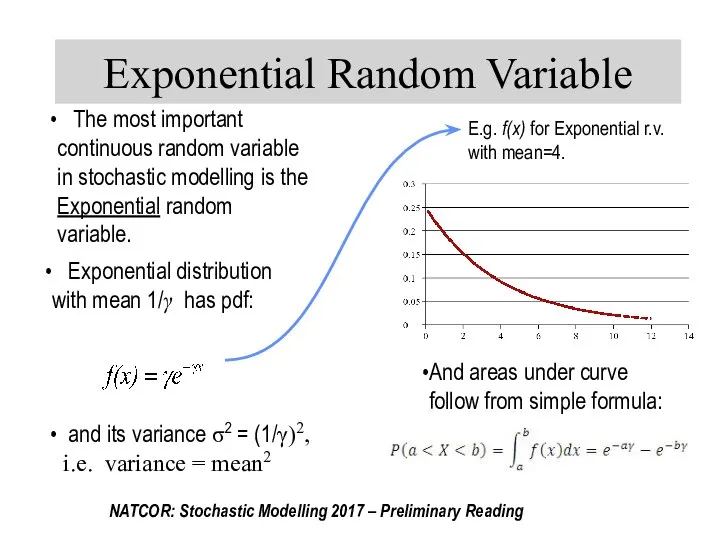
- 30. Exponential Random Variable The most important continuous random variable in stochastic modelling is the Exponential random
- 31. The General Theory: When ‘events’ of interest occur ‘at random’ at rate λ per unit time
- 32. Exponential Example THEORY IF Events occur ‘at random’, at rate A per unit time. THEN: Time
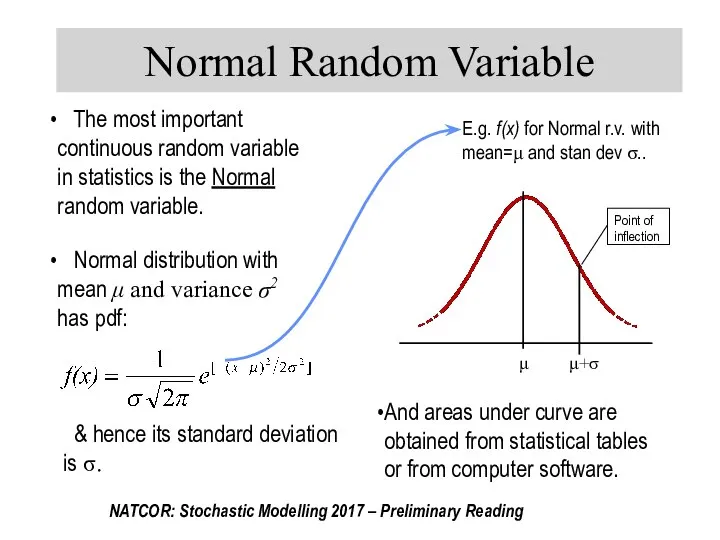
- 33. Normal Random Variable The most important continuous random variable in statistics is the Normal random variable.
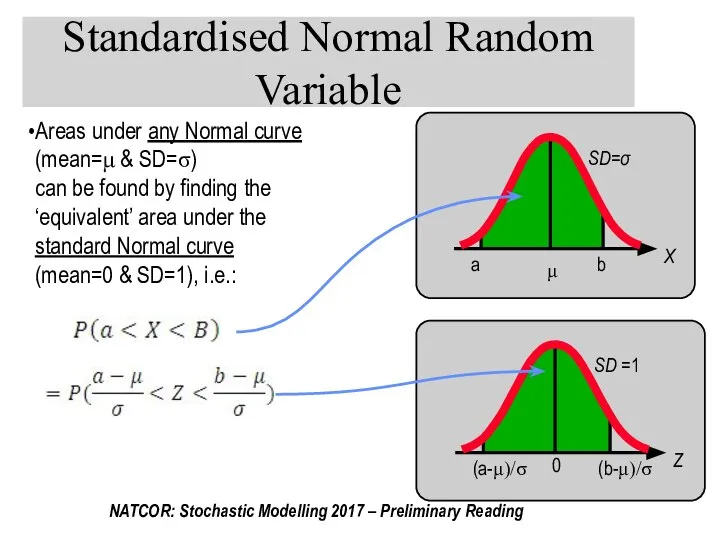
- 34. Standardised Normal Random Variable Areas under any Normal curve (mean=μ & SD=σ) can be found by
- 36. Скачать презентацию


























 Скрещивающиеся прямые
Скрещивающиеся прямые Исследование систем уравнений, содержащих параметр.
Исследование систем уравнений, содержащих параметр. Треугольник. Элементы треугольника
Треугольник. Элементы треугольника Вейвлет-преобразование изображений
Вейвлет-преобразование изображений Лекция 1. Дифференциальное исчисление функции одной переменной
Лекция 1. Дифференциальное исчисление функции одной переменной Векторы в пространстве
Векторы в пространстве Показательная функция, уравнения, неравенства
Показательная функция, уравнения, неравенства Двугранный угол. Задания для устного счета. Упражнение 8
Двугранный угол. Задания для устного счета. Упражнение 8 Отбор корней тригонометрического уравнения с помощью окружности
Отбор корней тригонометрического уравнения с помощью окружности Теорема синусов
Теорема синусов Случаи сложения вида +5, +6
Случаи сложения вида +5, +6 Алгебра. Исторический очерк
Алгебра. Исторический очерк Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений Параллельность прямых
Параллельность прямых Параллелограмм. (8 класс)
Параллелограмм. (8 класс) Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Параллелепипед. Куб
Параллелепипед. Куб Множества. Операции над множествами
Множества. Операции над множествами МАТЕМАТИКА
МАТЕМАТИКА  Презентация по математике "Числа от 1 до 100" - скачать бесплатно
Презентация по математике "Числа от 1 до 100" - скачать бесплатно Преобразование графиков функций
Преобразование графиков функций Бізді қоршаған әлемдегі үшбұрыштар
Бізді қоршаған әлемдегі үшбұрыштар Обыкновенные дроби. Правила сравнения дробей
Обыкновенные дроби. Правила сравнения дробей Линейная функция. Прямая пропорциональность, взаимное расположение графиков функций. 7 класс
Линейная функция. Прямая пропорциональность, взаимное расположение графиков функций. 7 класс Координаты на плоскости. 6 класс
Координаты на плоскости. 6 класс Различные способы решения тригонометрических неравенств
Различные способы решения тригонометрических неравенств Степень с натуральным показателем. Задания
Степень с натуральным показателем. Задания Математическая викторина. 5 – 6 классы
Математическая викторина. 5 – 6 классы