Содержание
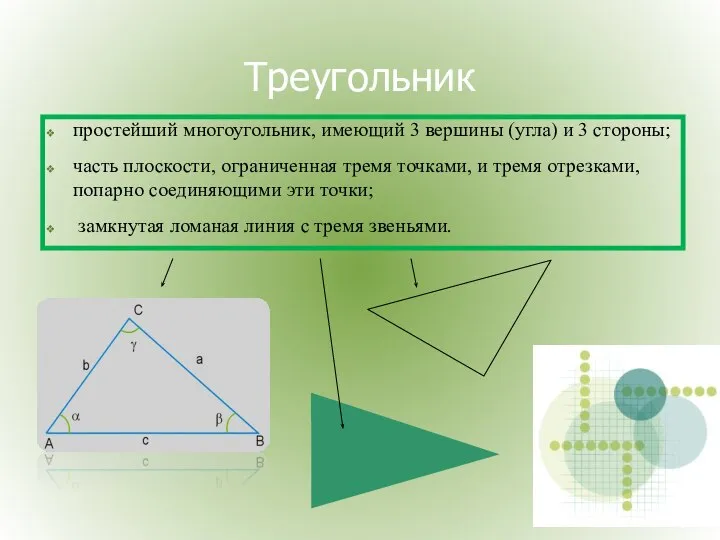
- 2. простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя
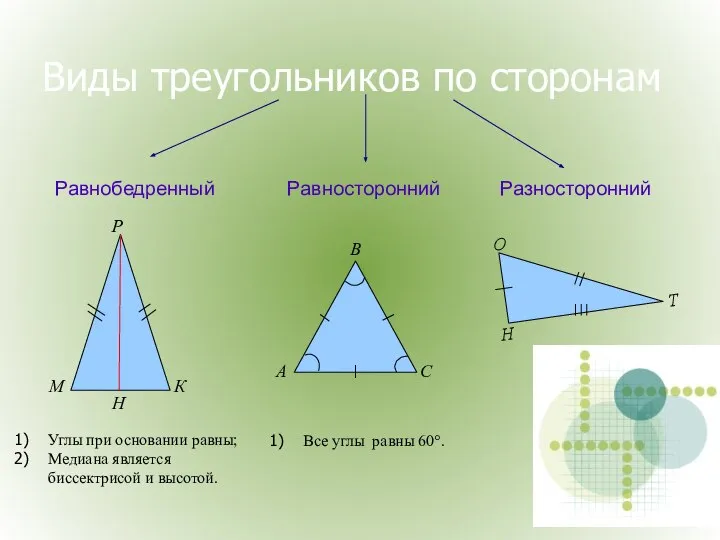
- 3. Виды треугольников по сторонам Равносторонний Равнобедренный Разносторонний Углы при основании равны; Медиана является биссектрисой и высотой.
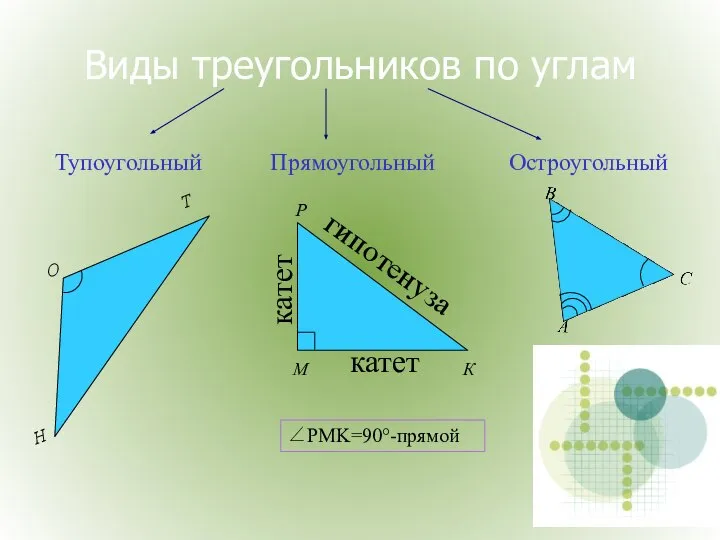
- 4. Виды треугольников по углам Прямоугольный Тупоугольный Н О Т Остроугольный катет катет гипотенуза ∠PMK=90°-прямой
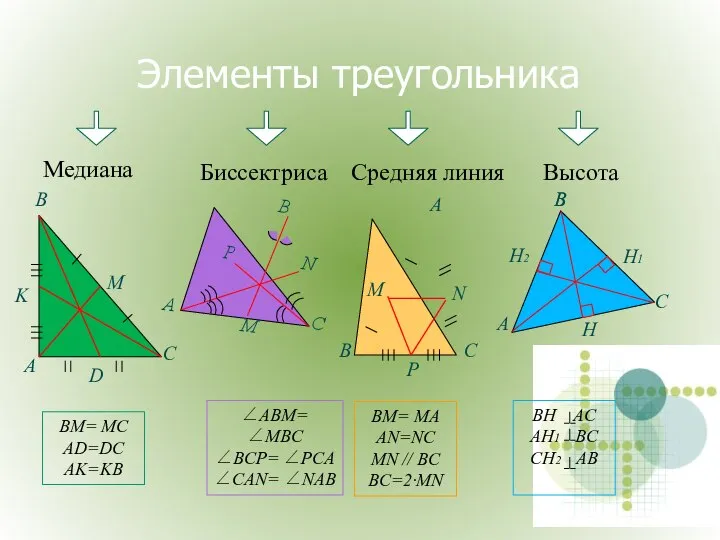
- 5. Элементы треугольника Медиана Высота Биссектриса Средняя линия BM= MC AD=DC AK=KB BM= MA AN=NC MN //
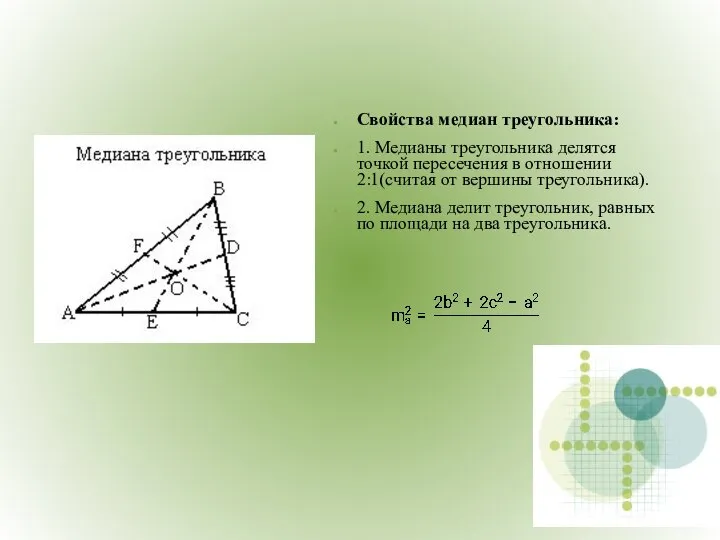
- 6. Свойства медиан треугольника: 1. Медианы треугольника делятся точкой пересечения в отношении 2:1(считая от вершины треугольника). 2.
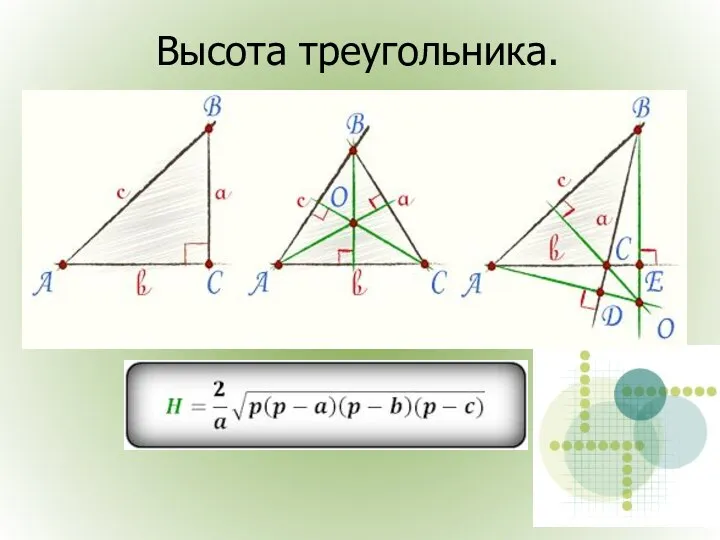
- 7. Высота треугольника.
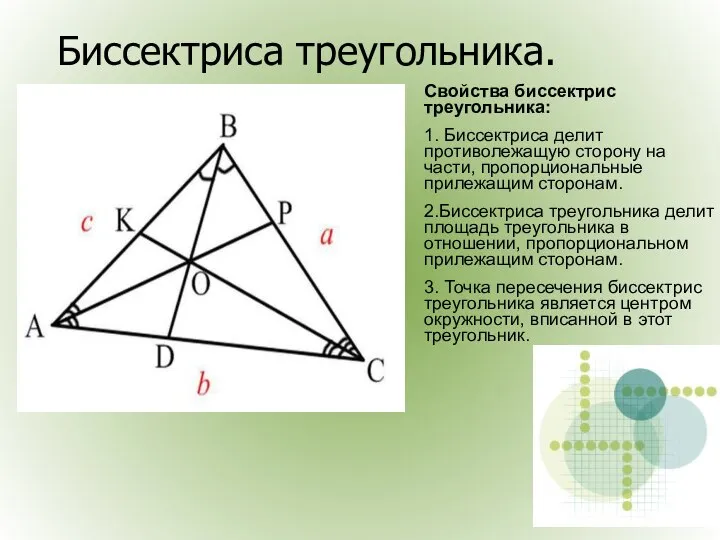
- 8. Биссектриса треугольника. Свойства биссектрис треугольника: 1. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. 2.Биссектриса
- 9. Средняя линия Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Свойство средней линии треугольника
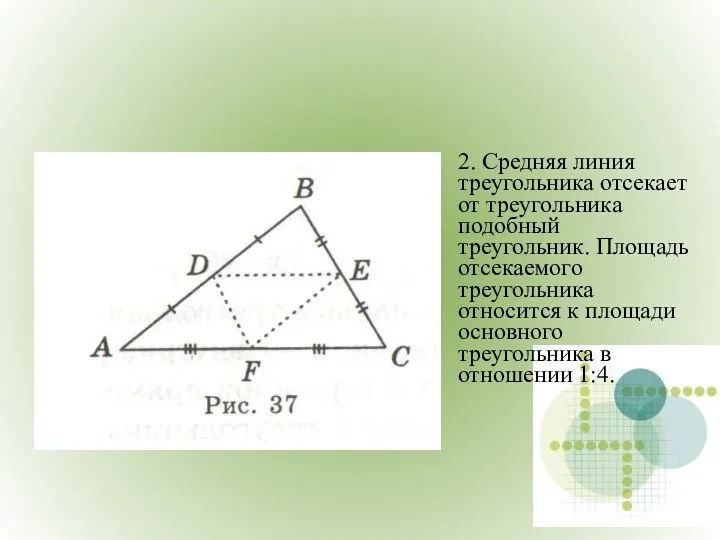
- 10. 2. Средняя линия треугольника отсекает от треугольника подобный треугольник. Площадь отсекаемого треугольника относится к площади основного
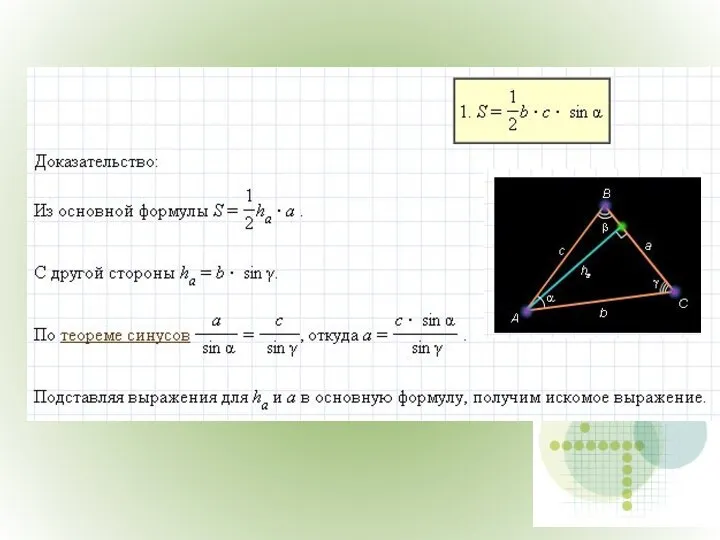
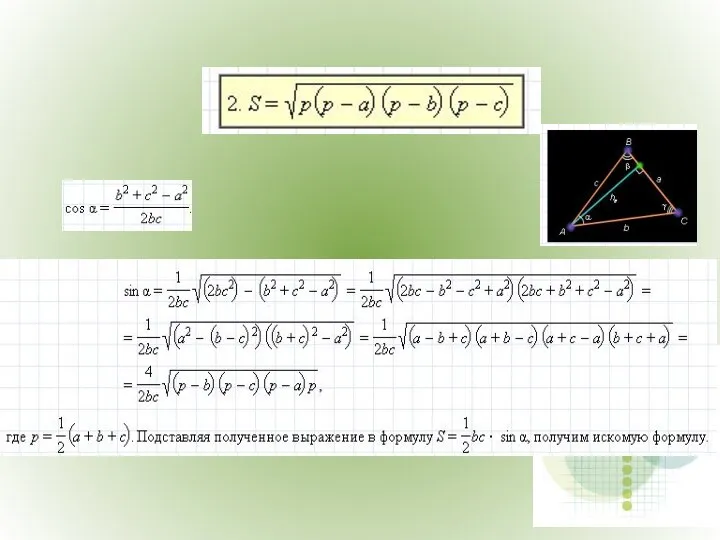
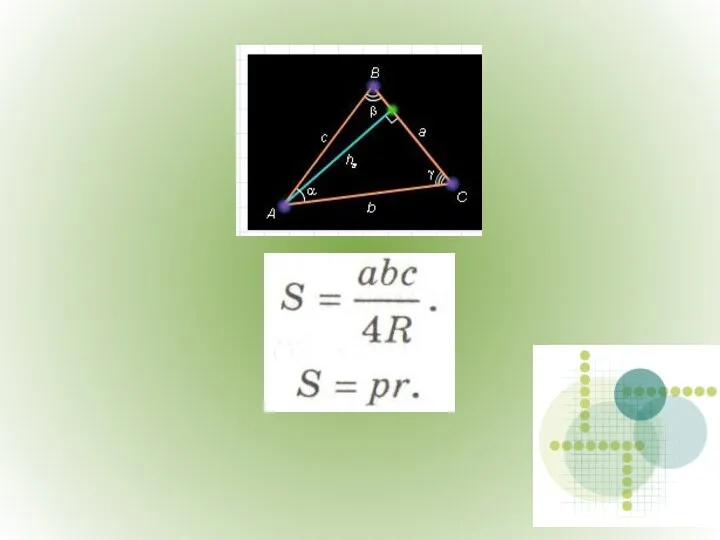
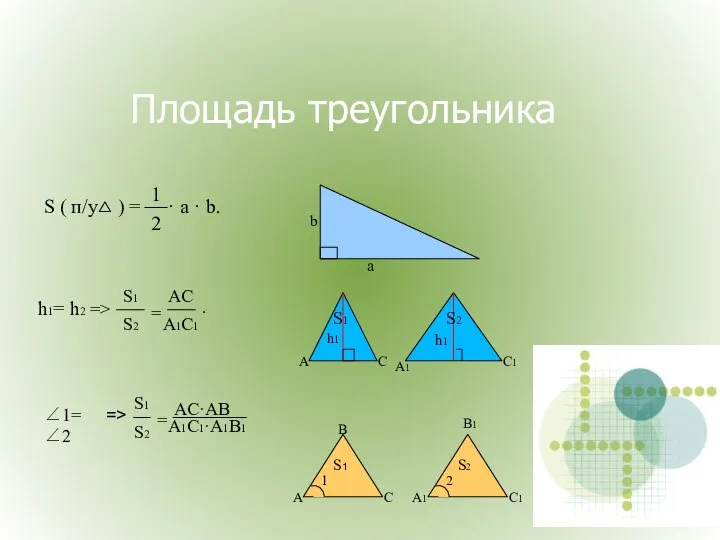
- 12. Площадь треугольника.
- 16. Площадь треугольника
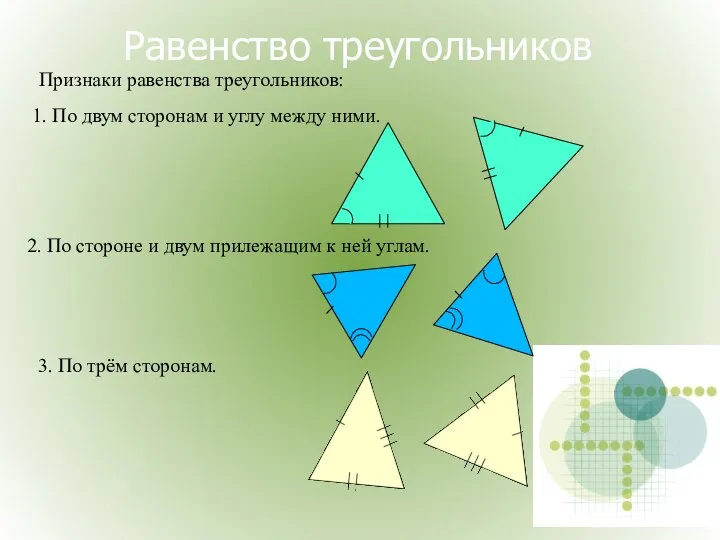
- 17. Равенство треугольников Признаки равенства треугольников: 2. По стороне и двум прилежащим к ней углам. 3. По
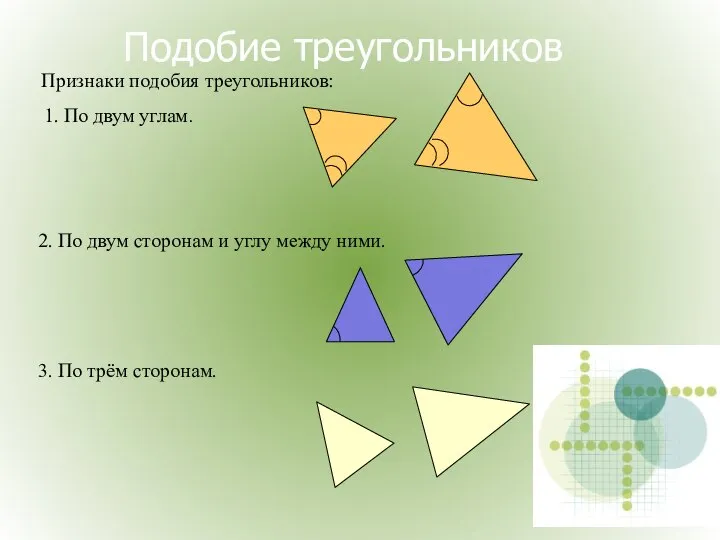
- 18. Подобие треугольников Признаки подобия треугольников: 1. По двум углам. 2. По двум сторонам и углу между
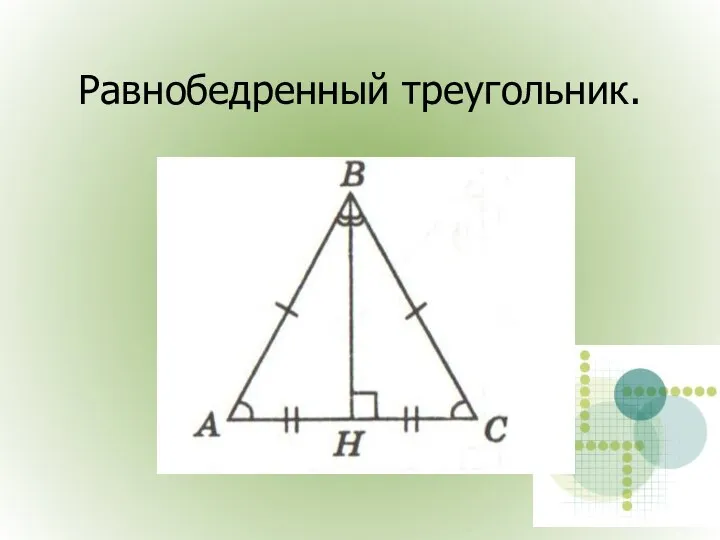
- 19. Равнобедренный треугольник.
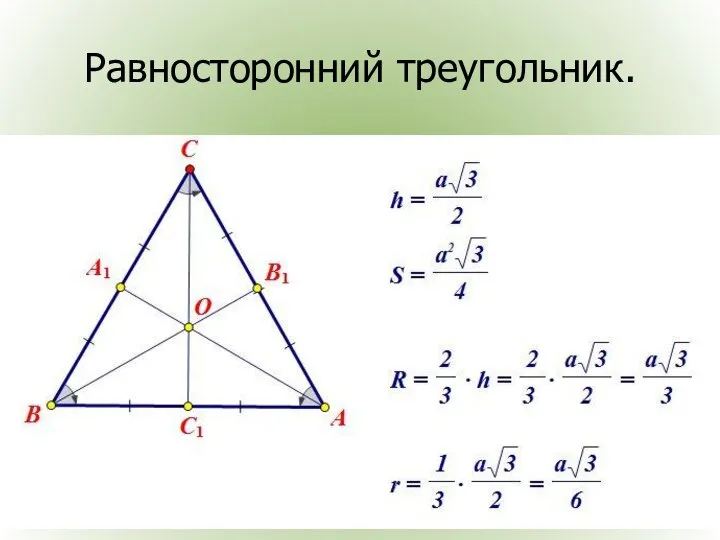
- 20. Равносторонний треугольник.
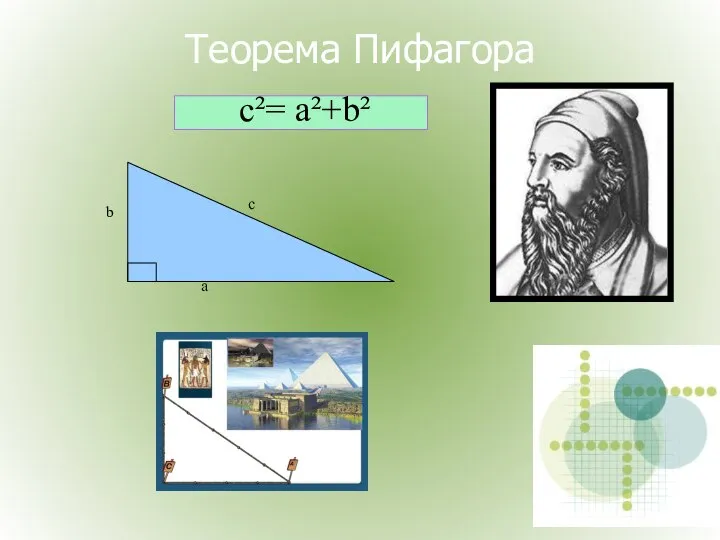
- 21. Теорема Пифагора c²= а²+b²
- 22. Доказательство теоремы Пифагора Дано: а,b- катеты, с-гипотенуза. Доказать: a2+b2=c2. Доказательство: Достроим до квадрата со стороной (a+b).
- 23. Вот задача индийского математика 12в. Бхаскары На берегу реки рос тополь одинокий. Вдруг ветра порыв его
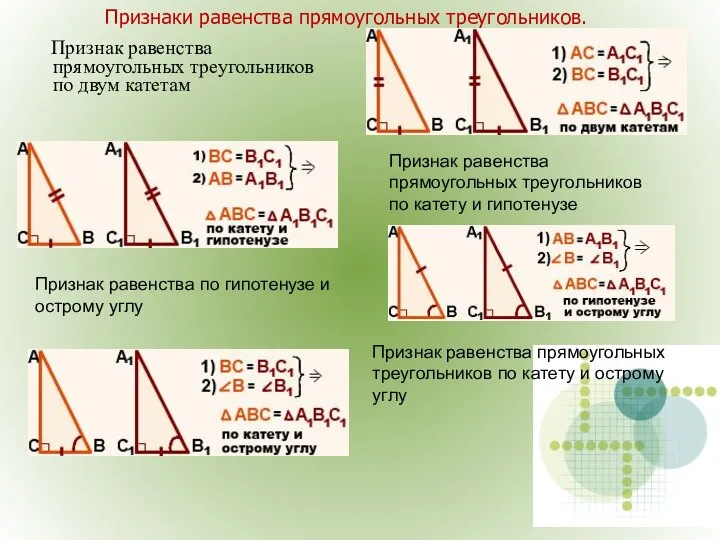
- 24. Признаки равенства прямоугольных треугольников. Признак равенства прямоугольных треугольников по двум катетам Признак равенства прямоугольных треугольников по
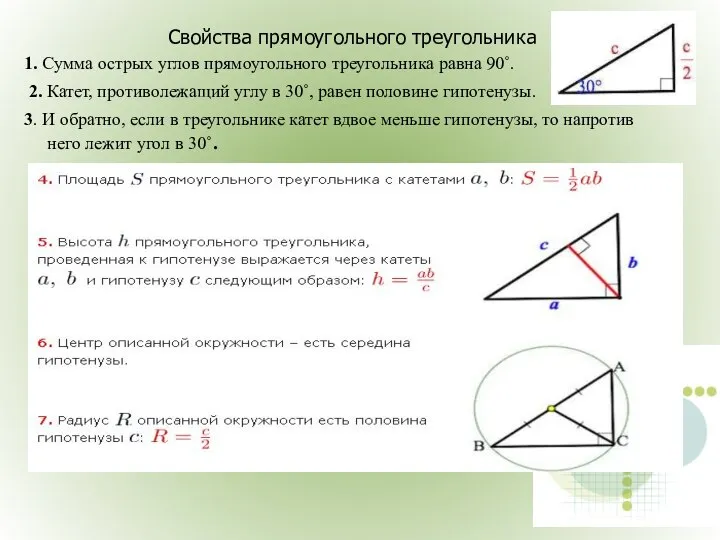
- 25. Свойства прямоугольного треугольника 1. Сумма острых углов прямоугольного треугольника равна 90˚. 2. Катет, противолежащий углу в
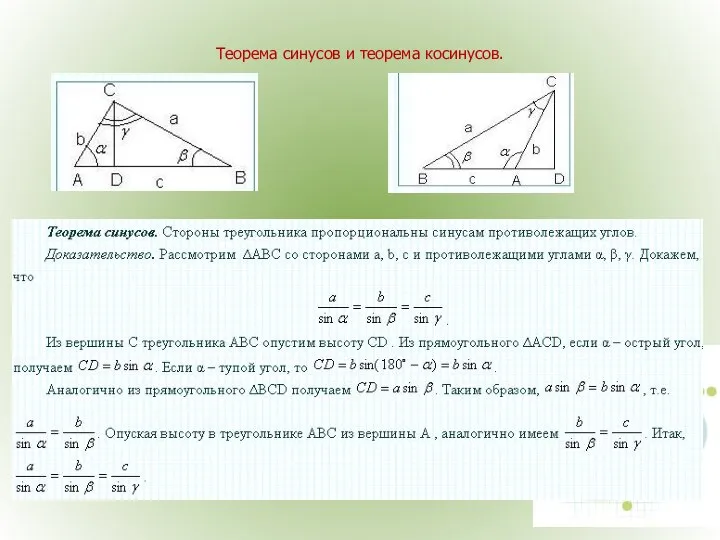
- 26. Теорема синусов и теорема косинусов.
- 27. Теорема косинусов.
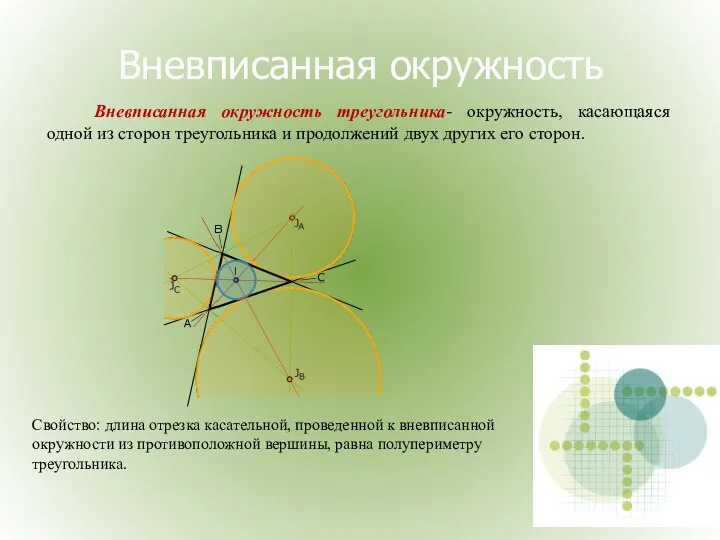
- 28. Вневписанная окружность Вневписанная окружность треугольника- окружность, касающаяся одной из сторон треугольника и продолжений двух других его
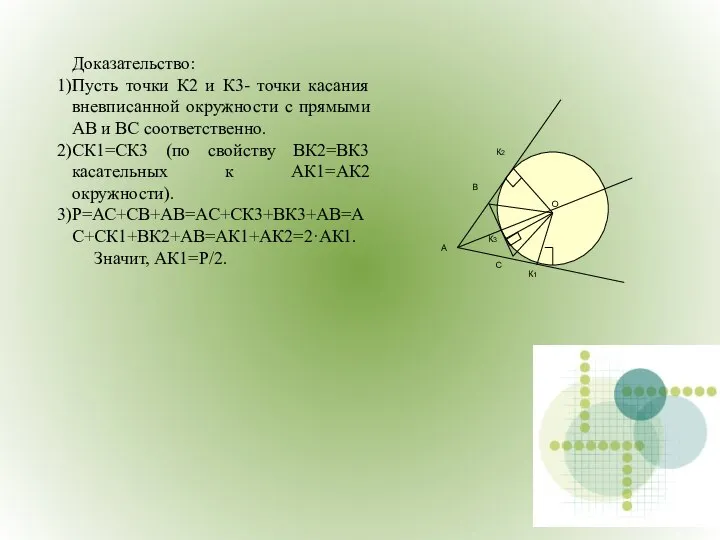
- 29. Доказательство: Пусть точки К2 и К3- точки касания вневписанной окружности с прямыми АВ и ВС соответственно.
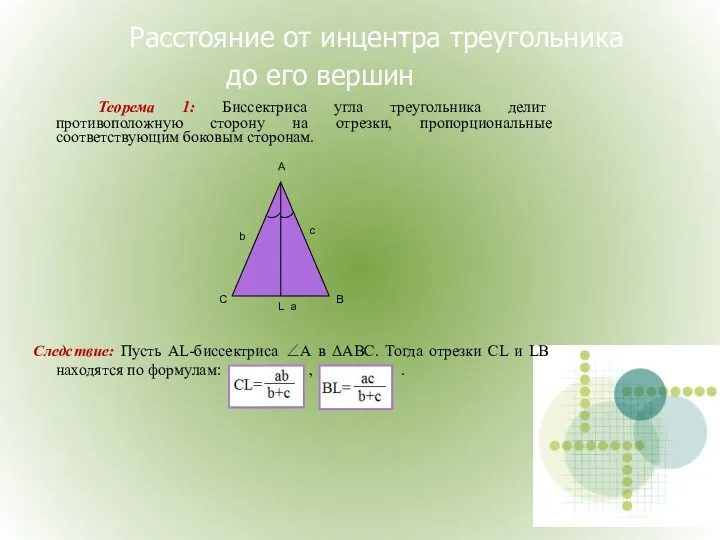
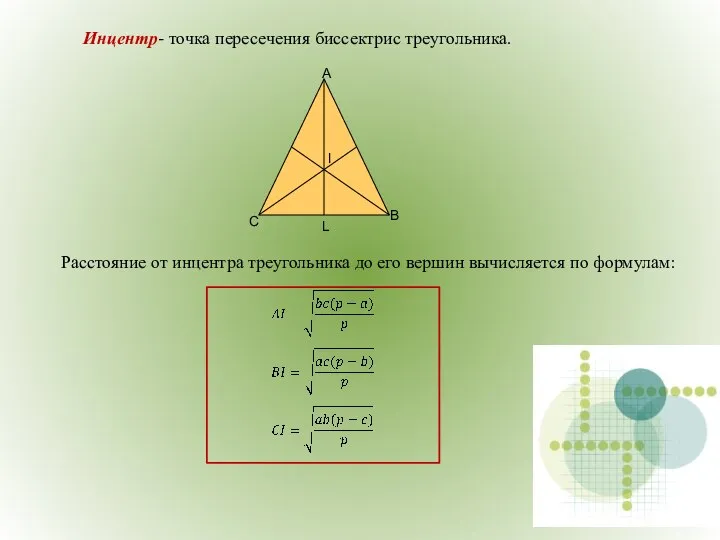
- 30. Расстояние от инцентра треугольника до его вершин Теорема 1: Биссектриса угла треугольника делит противоположную сторону на
- 31. Дано: ВК- биссектриса, СМ||ВК Доказательство: Так как ВК – биссектриса ∠АВС, то ∠АВК=∠КВС. Далее, ∠АВК=∠ВМС, как
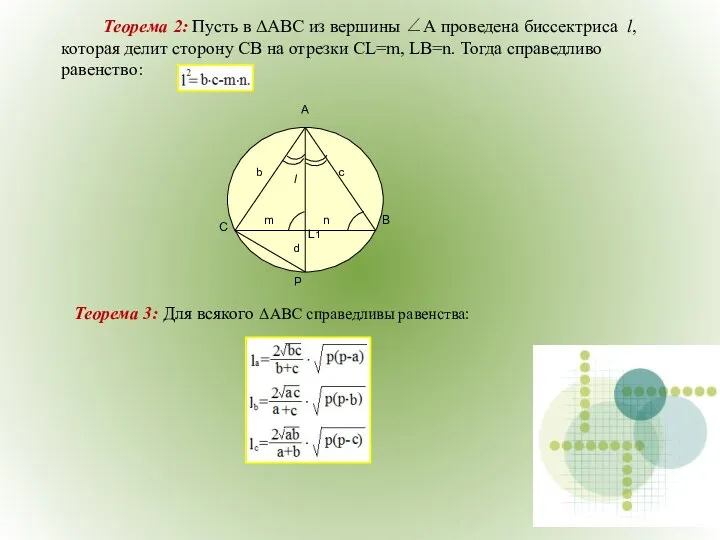
- 32. Теорема 2: Пусть в ΔАВС из вершины ∠А проведена биссектриса l, которая делит сторону СВ на
- 33. Инцентр- точка пересечения биссектрис треугольника. Расстояние от инцентра треугольника до его вершин вычисляется по формулам:
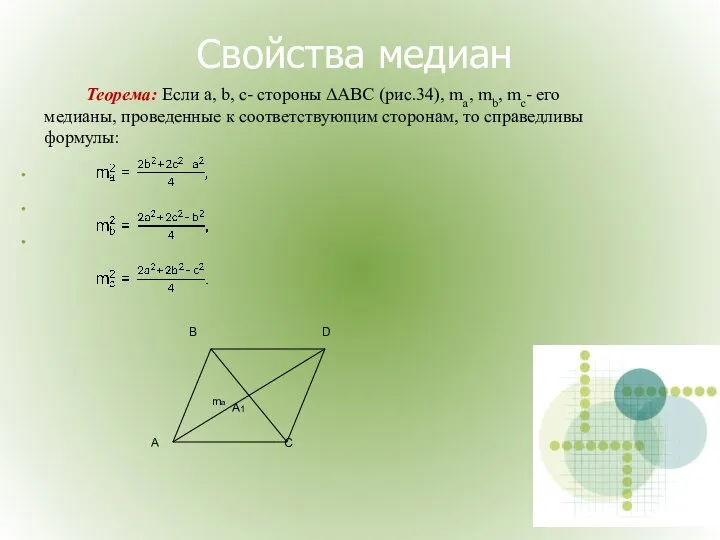
- 34. Свойства медиан Теорема: Если a, b, с- стороны ΔАВС (рис.34), ma, mb, mc- его медианы, проведенные
- 37. Задача
- 38. Спасибо за внимание!
- 40. Скачать презентацию











 Определенный интеграл
Определенный интеграл  Московский центр качества образования. Интернет-тестирование
Московский центр качества образования. Интернет-тестирование Презентация по математике "Муравьиные алгоритмы" - скачать
Презентация по математике "Муравьиные алгоритмы" - скачать  Десятичные дроби. 5 класс
Десятичные дроби. 5 класс Многогранники вокруг нас или мы внутри многогранника
Многогранники вокруг нас или мы внутри многогранника Решение систем линейных уравнений с двумя переменными. Способ подстановки
Решение систем линейных уравнений с двумя переменными. Способ подстановки Законы арифметических действий. Распределительный закон 5 класс
Законы арифметических действий. Распределительный закон 5 класс Қозғалыс жылдамдығы. Жылдамдықтың өлшем бірліктері
Қозғалыс жылдамдығы. Жылдамдықтың өлшем бірліктері Теория вероятностей. Задачи на вероятность
Теория вероятностей. Задачи на вероятность Математика. Закрепление. Внетабличное умножение и деление
Математика. Закрепление. Внетабличное умножение и деление Метод анализа иерархий. Методика метода МАИ
Метод анализа иерархий. Методика метода МАИ Открытый урок по алгебре в 11 классе по теме «Показательные уравнения»
Открытый урок по алгебре в 11 классе по теме «Показательные уравнения» Квадрат
Квадрат Логарифмические уравнения
Логарифмические уравнения Правильные многогранники и элементы их симметрии
Правильные многогранники и элементы их симметрии Решение задач на вычисление площади поверхности призмы
Решение задач на вычисление площади поверхности призмы Движение
Движение Площадь. Единицы площади
Площадь. Единицы площади Понятие вектора, его длины, коллинеарных и равных векторов
Понятие вектора, его длины, коллинеарных и равных векторов Проценты. 5 класс
Проценты. 5 класс Теория погрешностей, случайные и систематические погрешности
Теория погрешностей, случайные и систематические погрешности Определение значений коэффициентов квадратичной функции по графику
Определение значений коэффициентов квадратичной функции по графику Решение простейших задач по теории вероятности
Решение простейших задач по теории вероятности Презентация по математике "Логические задачи 1 класс" - скачать бесплатно
Презентация по математике "Логические задачи 1 класс" - скачать бесплатно Исследование алфавита знаков для кодирования информации
Исследование алфавита знаков для кодирования информации Решение задач с помощью уравнений
Решение задач с помощью уравнений Развивающая игра-конкурс для учащихся 5 классов
Развивающая игра-конкурс для учащихся 5 классов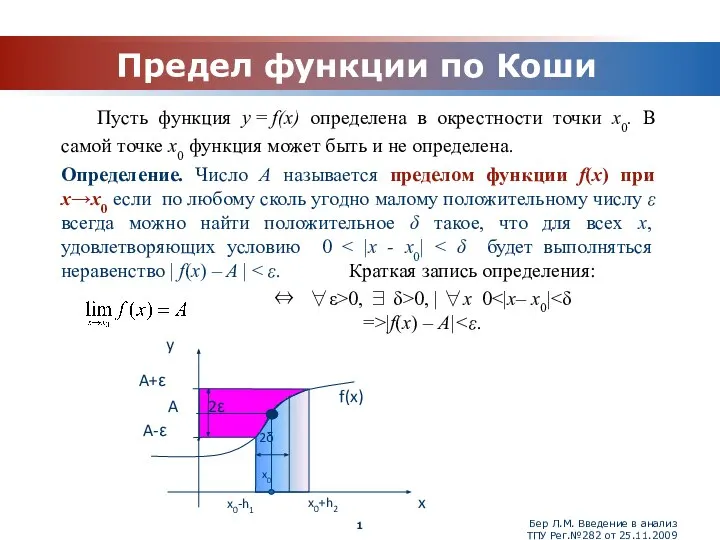 Предел функции по Коши
Предел функции по Коши