Содержание
- 2. Вопрос №1 Случайные погрешности и способы их обнаружения.
- 3. Случайные погрешности. Случайная погрешность – составная часть погрешности результата измерения, изменяющаяся случайно, незакономерно при проведении повторных
- 4. Формы задания закона распределения. Графическое изображение ряда распределения называют полигоном распределения случайной величины.
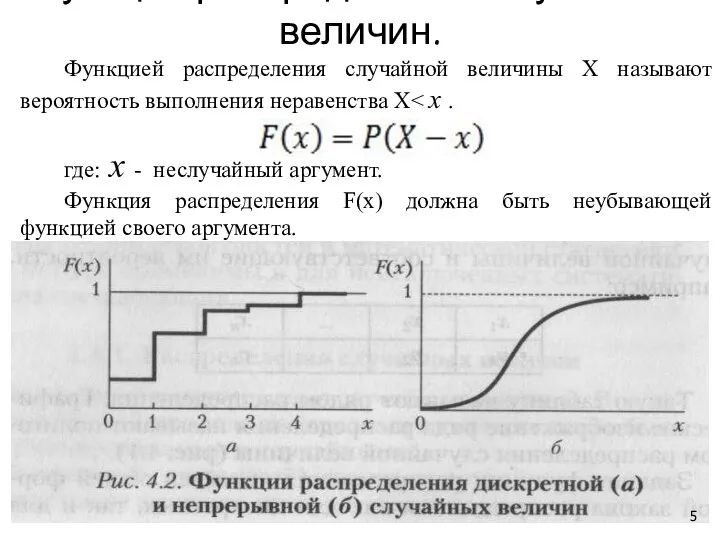
- 5. Функция распределения случайных величин. Функцией распределения случайной величины Х называют вероятность выполнения неравенства Х где: х
- 6. Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего предполагает знание аналитической модели
- 7. Числовые характеристики случайных величин. Для изучения распределения случайных величин пользуются рядом числовых характеристик: мер положения и
- 8. Закон нормального распределения. Теорема закона нормального распределения: если случайная величина Х представляет сумму очень большого числа
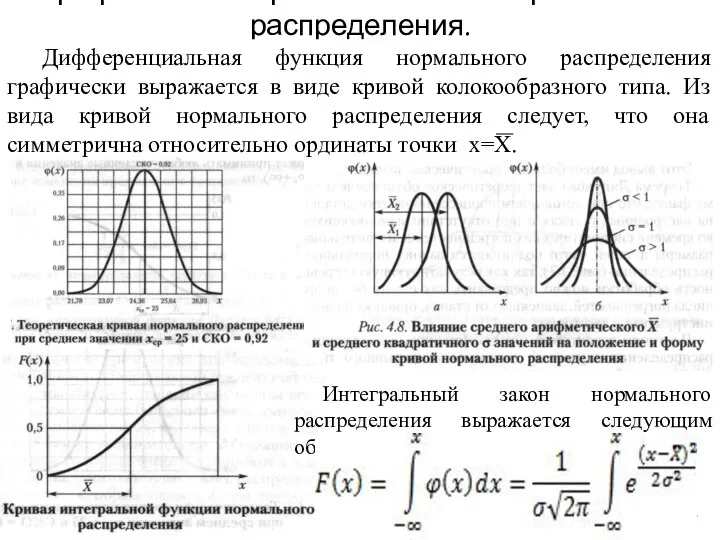
- 9. Графическое выражение закона нормального распределения. Дифференциальная функция нормального распределения графически выражается в виде кривой колокообразного типа.
- 10. Для оценки отклонений эмпирического распределения от нормального используются безразмерные характеристики: коэффициент асимметрии α и коэффициент эксцесса
- 11. Закон равномерного распределения. Равномерным распределением называют такое распределение случайной величины, когда она с одинаковой вероятностью может
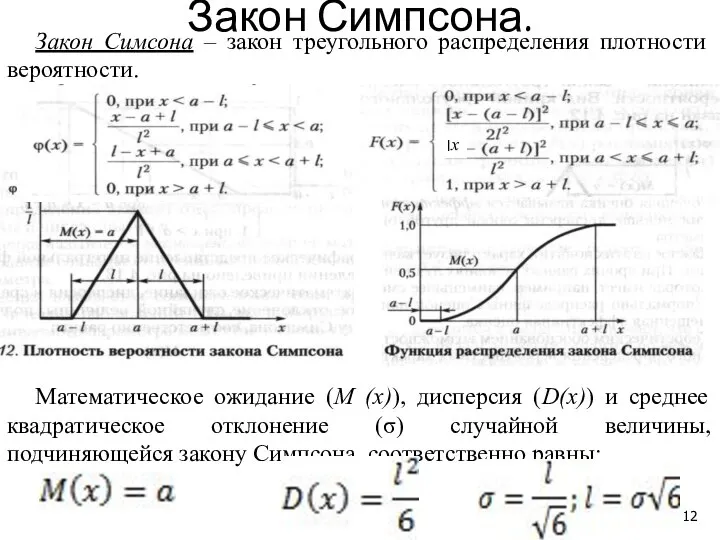
- 12. Закон Симсона – закон треугольного распределения плотности вероятности. Математическое ожидание (М (x)), дисперсия (D(x)) и среднее
- 13. Интервальные оценки числовых характеристик. Интервал значений случайной величины, внутри которого с заданной вероятностью находиться истинное значение
- 14. Интервальные оценки числовых характеристик. С достаточной для практических целей точностью значение tp можно определить по следующим
- 15. Пример интервальной оценки числовых характеристик. По выборке из n=20 найдено = 19,235 и s=0,08. Определить значение
- 16. Вопрос №2 Критерии для исключения систематических погрешностей.
- 17. Критерии для исключения систематических погрешностей. Способ последовательных разностей. Переменные систематические погрешности могут быть выявлены средствами статического
- 18. Расчеты критического значения критерия Аббе. Таблица критических значений критерия Аббе (Аq,n) Аппроксимирующие уравнения по расчету критических
- 19. Для некоторой величины имеем результаты измерений, выполненных через равные промежутки времени. Определяем значение D(x) и Q(x)
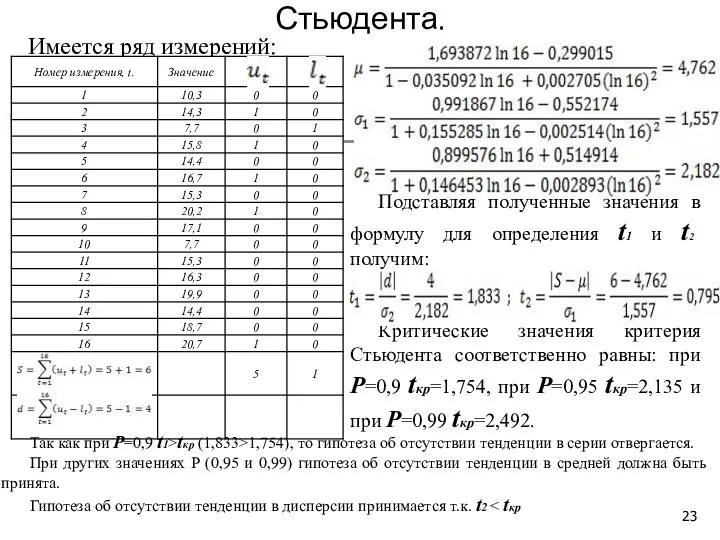
- 20. Одним из самых простых, дающих практически надежные результаты является метод, предложенный Фостером и Стьюдентом. Суть метода
- 21. Гипотеза о наличии тенденции проверяется с помощью критерия Стьюдента: где: μ – математическое ожидание величины S,
- 22. Критические значения критерия Стьюдента tкр определяются в зависимости от принятого значения доверительной вероятности Р. При Р=0,9
- 23. Имеется ряд измерений: Пример применения метода Фостера – Стьюдента. Подставляя полученные значения в формулу для определения
- 24. Вопрос №3 Формы представления результатов измерения.
- 25. Необходимо пользоваться основным правилом: погрешность, получаемая в результате вычислений, должна быть на порядок (в 10 раз)
- 27. Скачать презентацию




















 20180127_dm_8_koordinaty_na_pryamoy
20180127_dm_8_koordinaty_na_pryamoy Построение точек, линий и направлений
Построение точек, линий и направлений Математика в профессиональной деятельности
Математика в профессиональной деятельности Деление дробей
Деление дробей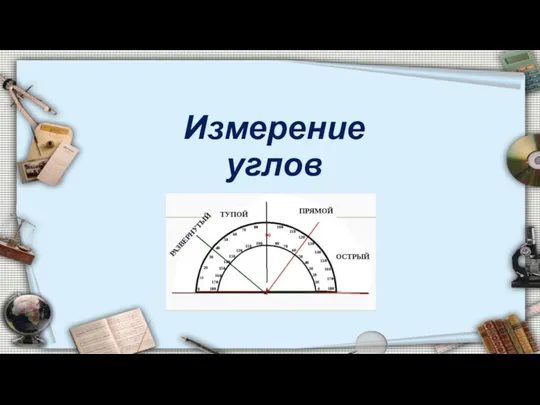 Измерение углов
Измерение углов Презентация по математике "Повторение курса математики." - скачать бесплатно
Презентация по математике "Повторение курса математики." - скачать бесплатно Центральный и вписанные углы
Центральный и вписанные углы Аттестационная работа. Математика и искусство
Аттестационная работа. Математика и искусство Конус та його елементи
Конус та його елементи Занимательная таблица умножения
Занимательная таблица умножения Projekts “Matemātika 6. klasei”
Projekts “Matemātika 6. klasei” Проецирование правильных треугольных и шестиугольных призм
Проецирование правильных треугольных и шестиугольных призм Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Systems of linear algebraic equations
Systems of linear algebraic equations Упрощение выражений (5 класс)
Упрощение выражений (5 класс)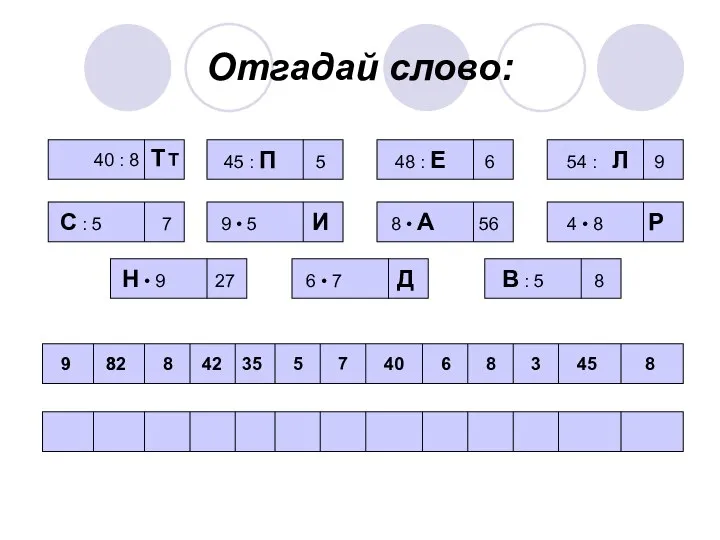 Математика
Математика Харди-Вайнберг заңы
Харди-Вайнберг заңы Летим в математическую галактику
Летим в математическую галактику Логические задачи
Логические задачи Объем призмы. Решение задач
Объем призмы. Решение задач презентация матеша
презентация матеша Лист Мёбиуса
Лист Мёбиуса Прибавление суммы к числу
Прибавление суммы к числу Решение задач с применением систем линейных уравнений
Решение задач с применением систем линейных уравнений Основные понятия Основные понятия Компоненты арифметических действий и нахождение неизвестных компонентов - при сложении - при
Основные понятия Основные понятия Компоненты арифметических действий и нахождение неизвестных компонентов - при сложении - при  Натуральные числа. Десятичная система счисления
Натуральные числа. Десятичная система счисления Симметрия и её виды
Симметрия и её виды