Содержание
- 2. Прямая задача теории погрешности. Пример. Найти предельную абсолютную и относительную погрешности объёма шара , если диаметр
- 3. Суть - оценивание погрешностей аргументов произвольной функции нескольких переменных, обеспечивающих заданную или меньшую погрешность функции. В
- 4. Обратная задача теории погрешности. Пример.
- 5. Тема: Вычисление значений функций 2. Вычисление значения алгебраического полинома. Схема Горнера. Рассмотрим полином Наша задача –
- 6. Сравним эффективность предложенного варианта вычислений (схемы Горнера) с прямым вычислением «в лоб». В качестве критерия будем
- 7. Тема: Вычисление значений функций Покажем, что числа являются коэффициентами полинома Q(x), полученного в качестве частного при
- 8. Определение. Числовой ряд называется сходящимся, если существует предел последовательности его частных сумм , где . Задача.
- 9. Процедура вычислений. Выбираем три положительных числа ε1, ε2, ε3, таких, что 1) остаточная погрешность (ε1) :
- 10. Тогда для частичной суммы погрешность действий (суммирования) удовлетворяет неравенству 3) Погрешность при округлении результата (ε3) .
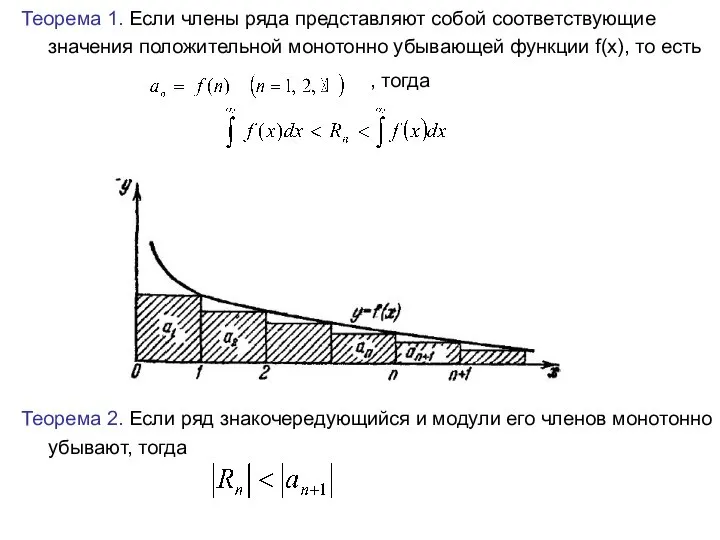
- 11. Теорема 1. Если члены ряда представляют собой соответствующие значения положительной монотонно убывающей функции f(x), то есть
- 12. Найти сумму ряда с точностью 0,004. Решение. Округлять результат и слагаемые не будем . Тогда погрешность
- 13. Функция f(x) аналитическая в точке x = ξ, если в окрестности этой точки она разлагается в
- 14. Если f(ξ) известно и требуется найти значение f(ξ + h), где h – «малая поправка», то
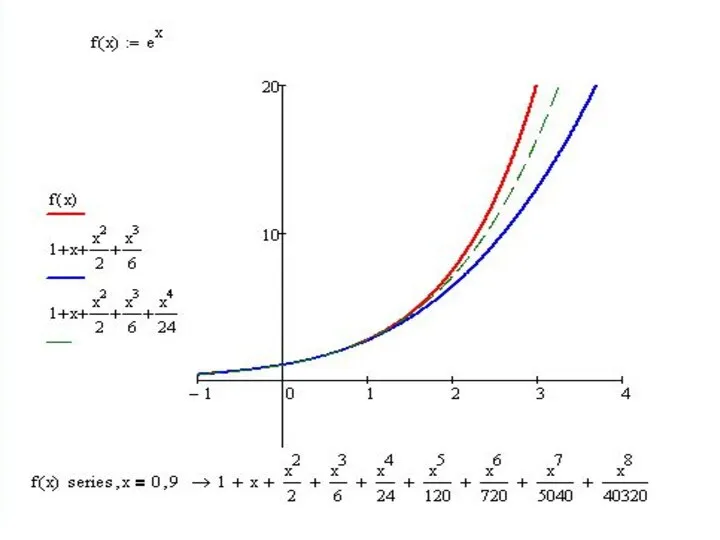
- 15. Вычисление экспоненты ( ех). Известно из курса математического анализа, что экспоненциальная функция в окрестности точки 0
- 17. Число е = 2.71828182… известно с очень высокой точностью. Поэтому величину еЕ(х) = е*е*е*…*е можно считать
- 18. Если учесть, что , то получим Если обозначить , un - последний сохраненный член частичной суммы,
- 20. Скачать презентацию















 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Понятие модели. Способы представления моделей. (Лекция 4)
Понятие модели. Способы представления моделей. (Лекция 4) Лента Мёбиуса
Лента Мёбиуса Time quiz
Time quiz Старинные системы мер
Старинные системы мер Признаки делимости на 2, 5, 10
Признаки делимости на 2, 5, 10 Вычитание из чисел 6, 7. Решение задач
Вычитание из чисел 6, 7. Решение задач Презентация Переменные процентные ставки В течение периода времени действует ставка простых процентов Начисленные проценты составят: В течение периода времени действует ставка простых процентов Начисленные проценты составят: ………………………………………
Презентация Переменные процентные ставки В течение периода времени действует ставка простых процентов Начисленные проценты составят: В течение периода времени действует ставка простых процентов Начисленные проценты составят: ………………………………………  Умножение отрицательных чисел. 6 класс
Умножение отрицательных чисел. 6 класс Сфера и шар. Решение задач
Сфера и шар. Решение задач Преобразования графиков функций
Преобразования графиков функций За страницами учебника 10 класс
За страницами учебника 10 класс Состав чисел первого десятка Автор: Акимова Елена Юрьевна учитель КОУ «Тарская гимназия №1 им. А.М.Луппова» Омско
Состав чисел первого десятка Автор: Акимова Елена Юрьевна учитель КОУ «Тарская гимназия №1 им. А.М.Луппова» Омско Наглядное представление статистической информации - диаграмма
Наглядное представление статистической информации - диаграмма Средние величины
Средние величины Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Деление на десятичную дробь
Деление на десятичную дробь Алгоритм решения биквадратного уравнения
Алгоритм решения биквадратного уравнения Элементы математической статистики. (Лекция 6)
Элементы математической статистики. (Лекция 6) Треугольники. Высота, медиана, биссектриса треугольника
Треугольники. Высота, медиана, биссектриса треугольника Математика и экономика. Задачи о наибольших и наименьших значениях величин
Математика и экономика. Задачи о наибольших и наименьших значениях величин Теория вероятностей. События. Виды событий. Вероятностное пространство. Вероятностные схемы: классическая, геометрическая
Теория вероятностей. События. Виды событий. Вероятностное пространство. Вероятностные схемы: классическая, геометрическая Этапы расчета прогнозных значений методом двойного скользящего среднего
Этапы расчета прогнозных значений методом двойного скользящего среднего Подготовка к контрольной работе №1
Подготовка к контрольной работе №1 Параллельные прямые. Работа на готовых чертежах
Параллельные прямые. Работа на готовых чертежах Окружающий нас мир – это мир геометрии
Окружающий нас мир – это мир геометрии Вписані та описані чотирикутники
Вписані та описані чотирикутники