Содержание
- 2. Подставляем найденные величины в ряд Маклорена:
- 3. Область сходимости ряда
- 4. 2
- 6. Производные четного порядка все равны нулю: Производные нечетного порядка равны: где Подставляем найденные величины в ряд
- 7. Область сходимости ряда
- 8. 3
- 10. Производные нечетного порядка все равны нулю: Производные четного порядка равны: где Подставляем найденные величины в ряд
- 11. Область сходимости ряда
- 12. 4
- 13. Следовательно:
- 14. Подставляем найденные величины в ряд Маклорена:
- 15. Интервал сходимости ряда
- 16. Этот ряд называется биномиальным. Если число m – целое и положительное, то биномиальный ряд представляет собой
- 17. 5
- 19. Область сходимости ряда
- 20. ПРИМЕР. Разложить в ряд функцию
- 22. Скачать презентацию


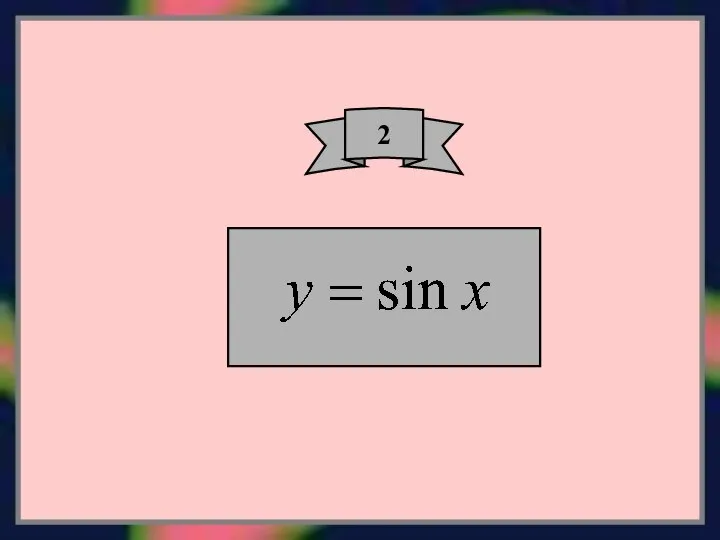
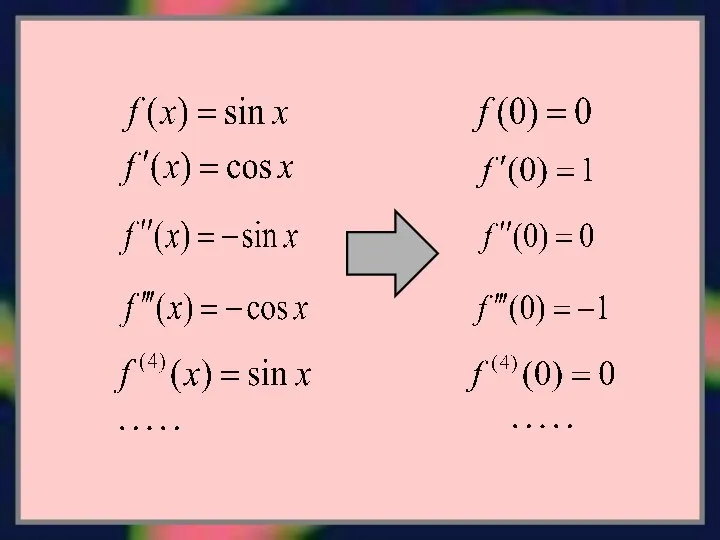


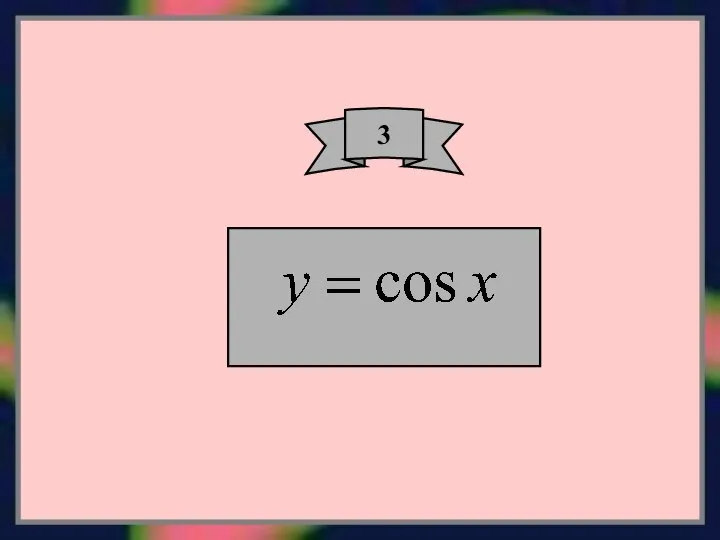
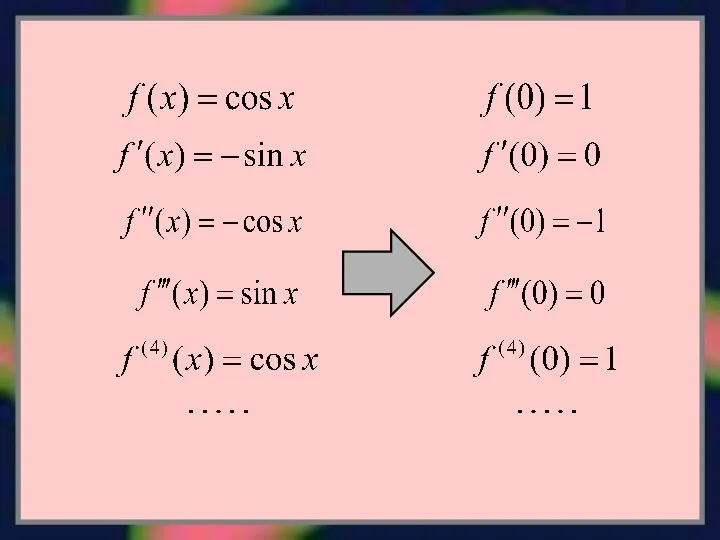


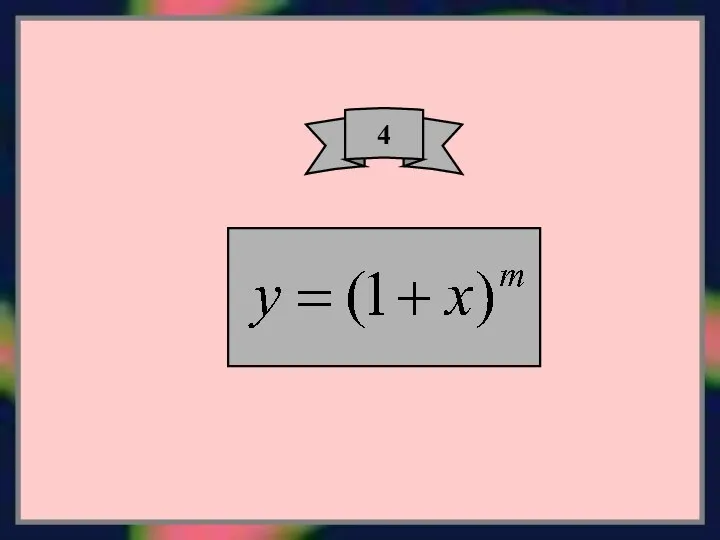




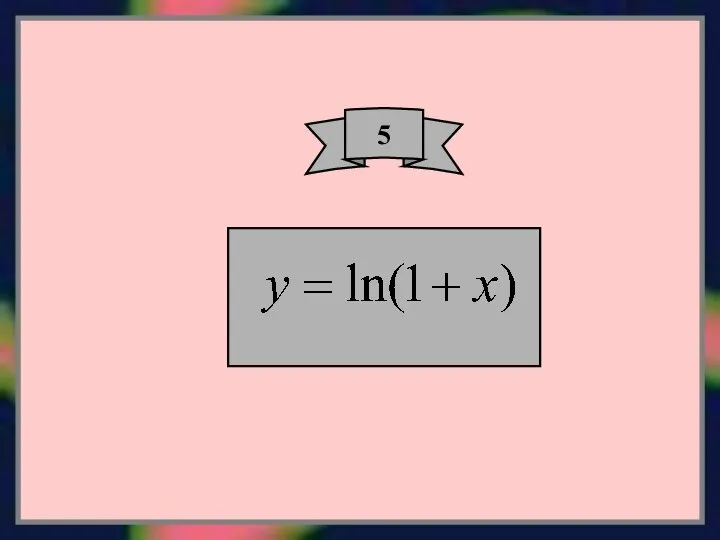



 Кто хочет стать математиком
Кто хочет стать математиком Закон больших чисел и центральная предельная теорема
Закон больших чисел и центральная предельная теорема Углы и диагонали многоугольников. 5 класс
Углы и диагонали многоугольников. 5 класс Формулы середины отрезка и расстояния между двумя точками
Формулы середины отрезка и расстояния между двумя точками Площадь криволинейной трапеции
Площадь криволинейной трапеции Схема Бернулли
Схема Бернулли Основні види моделювання. Формальні методи побудови моделей
Основні види моделювання. Формальні методи побудови моделей Теорема Виета
Теорема Виета Функциональное зонирование
Функциональное зонирование Решение систем уравнений методом введения новой переменной (9 класс)
Решение систем уравнений методом введения новой переменной (9 класс) Фунцияның туындысы мен дифференциалын қолдану
Фунцияның туындысы мен дифференциалын қолдану Теорема Пифагора
Теорема Пифагора Определение высоты здания
Определение высоты здания Число π (пи)
Число π (пи) Случаи вычитания 14 -
Случаи вычитания 14 - Натуральные числа
Натуральные числа Теорема Пифагора и ее применение при решении различных задач
Теорема Пифагора и ее применение при решении различных задач Признаки равенства треугольников
Признаки равенства треугольников Презентация по математике "Сложение дробей с одинаковыми знаменателями (5 класс)" - скачать
Презентация по математике "Сложение дробей с одинаковыми знаменателями (5 класс)" - скачать  Деление дробей. 8 класс
Деление дробей. 8 класс Третий признак равенства треугольников
Третий признак равенства треугольников Математика. Что такое периметр?
Математика. Что такое периметр? Ловушка фиктивных переменных
Ловушка фиктивных переменных Архитектура и геометрия
Архитектура и геометрия Презентация по математике "Нахождение наибольшего общего делителя чисел" - скачать
Презентация по математике "Нахождение наибольшего общего делителя чисел" - скачать  Пустыня ошибок
Пустыня ошибок Связь между суммой и слагаемыми
Связь между суммой и слагаемыми Использование ИКТ в обучении геометрии
Использование ИКТ в обучении геометрии