Содержание
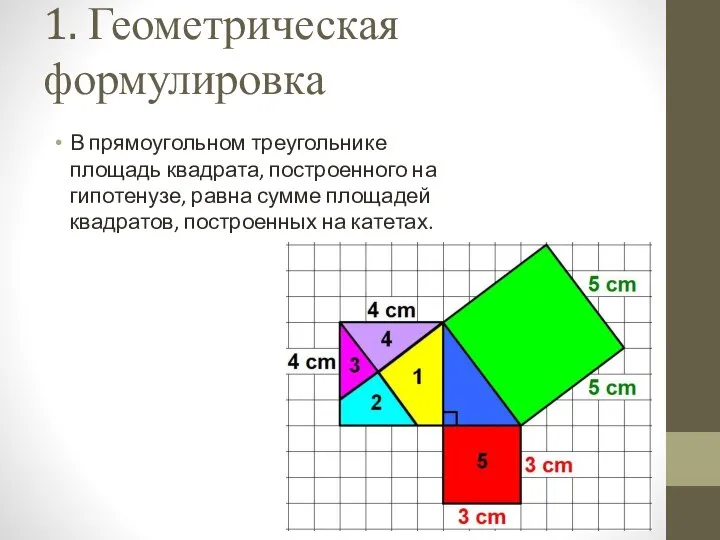
- 2. 1. Геометрическая формулировка В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных
- 3. 2.Алгебраический метод доказательства Площадь данного прямоугольного треугольника, с одной стороны, равна с другой , где p
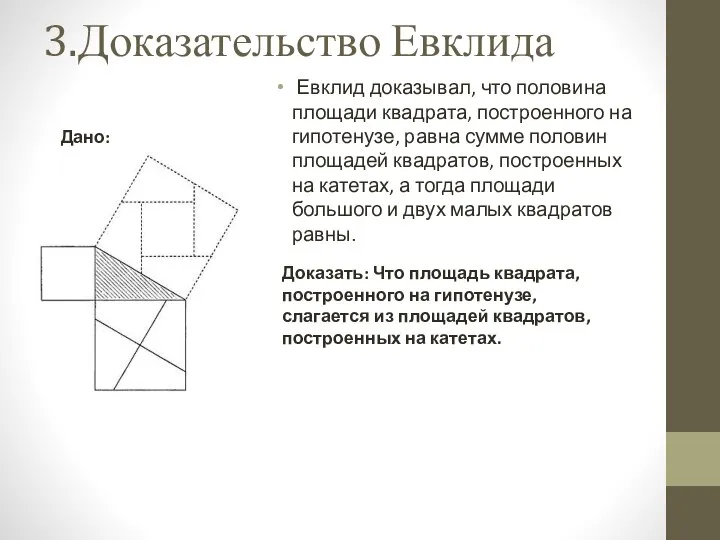
- 4. 3.Доказательство Евклида Евклид доказывал, что половина площади квадрата, построенного на гипотенузе, равна сумме половин площадей квадратов,
- 5. 3.Доказательство Евклида Рассмотрим чертёж => построены квадраты на сторонах прямоугольного треугольника и провели из вершины прямого
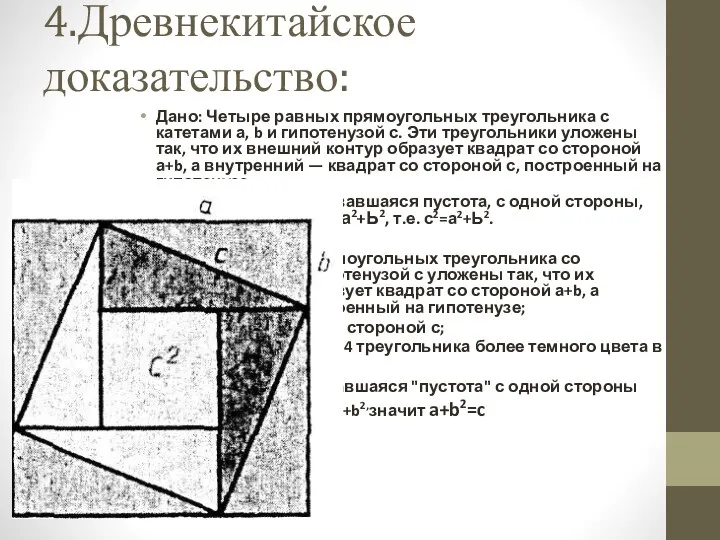
- 6. 4.Древнекитайское доказательство: Дано: Четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с. Эти треугольники
- 7. 5.Простейшее доказательство «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах». Простейшее
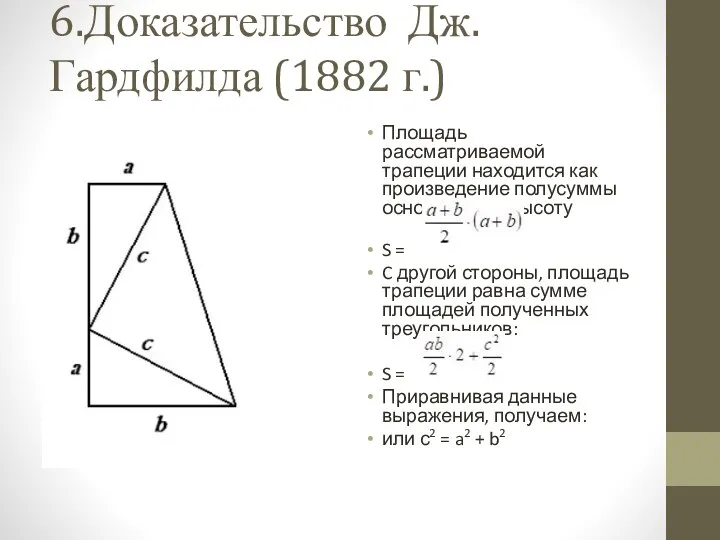
- 8. 6.Доказательство Дж. Гардфилда (1882 г.) Площадь рассматриваемой трапеции находится как произведение полусуммы оснований на высоту S
- 10. Скачать презентацию



 Тест по геометрии
Тест по геометрии Прямая и отрезок
Прямая и отрезок Треугольник. Правило треугольника
Треугольник. Правило треугольника Нахождение числа по его дроби
Нахождение числа по его дроби Проценты. 5 класс
Проценты. 5 класс признаки делимости на 10, на 5, на 2
признаки делимости на 10, на 5, на 2 Дискретная математика. Часть 4 Элементы математической логики
Дискретная математика. Часть 4 Элементы математической логики Умножение двузначного числа на однозначное
Умножение двузначного числа на однозначное Теория предикатов. Операции над предикатами
Теория предикатов. Операции над предикатами Сложение и вычитание натуральных чисел. (5 класс)
Сложение и вычитание натуральных чисел. (5 класс) Комбинаторика. Урок 151
Комбинаторика. Урок 151 Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю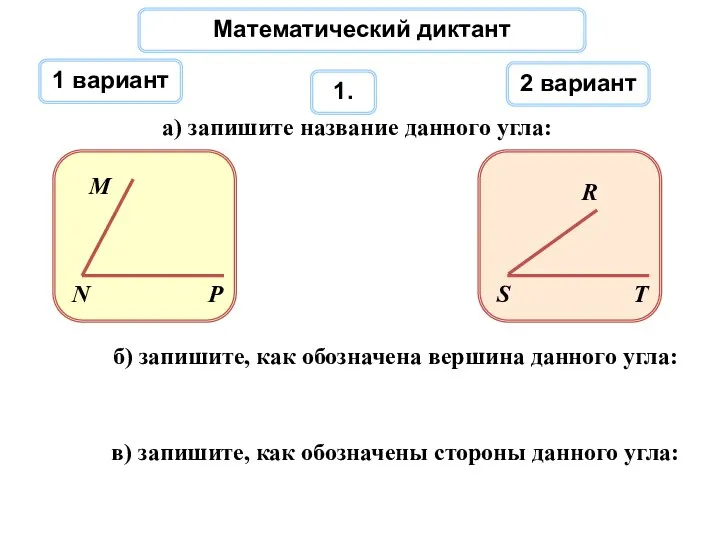 Углы. Математический диктант для 5а
Углы. Математический диктант для 5а Свойства и график функции y=sinх
Свойства и график функции y=sinх Исследовательская работа по теме: «Конус и его применение в быту»
Исследовательская работа по теме: «Конус и его применение в быту» Прикидка результата действий. Цифры разряда, до которого выполняется округление. (5 класс)
Прикидка результата действий. Цифры разряда, до которого выполняется округление. (5 класс) Змагання з усного рахунку. Міксіке
Змагання з усного рахунку. Міксіке Геометрия. Повторение
Геометрия. Повторение Построение двойственной задачи
Построение двойственной задачи Корреляция. Причинность. Детерминизм
Корреляция. Причинность. Детерминизм Математик - царица всех наук. Викторина
Математик - царица всех наук. Викторина Математическое ожидание
Математическое ожидание Прямая в пространстве
Прямая в пространстве  Открытый интегрированный урок математики с элементами Самопознания в 3-м «В» классе на тему: «Закрепление табличного умножени
Открытый интегрированный урок математики с элементами Самопознания в 3-м «В» классе на тему: «Закрепление табличного умножени Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Прямоугольник
Прямоугольник Раскрытие скобок. Коэффициент. Подобные слагаемые
Раскрытие скобок. Коэффициент. Подобные слагаемые Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями