- Главная
- Математика
- Решение нелинейного уравнения методом итерации

Содержание
- 2. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 3. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 4. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 5. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 6. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 7. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 8. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 9. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 10. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 11. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 12. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 13. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 14. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 15. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 16. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 17. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 18. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 19. 2.2.1 Решение нелинейного уравнения методом итерации Пусть дано уравнение f(x)=0. Для нахождения его корней методом итераций
- 21. Скачать презентацию
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
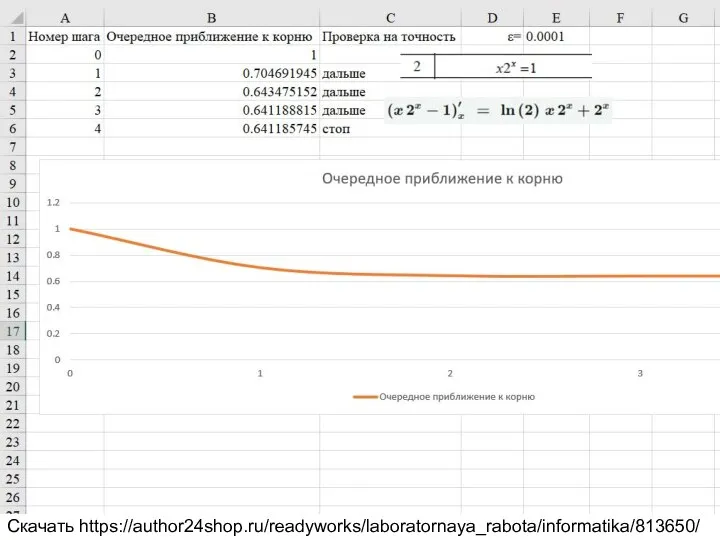
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 2.
x*2^x=1
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813650/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
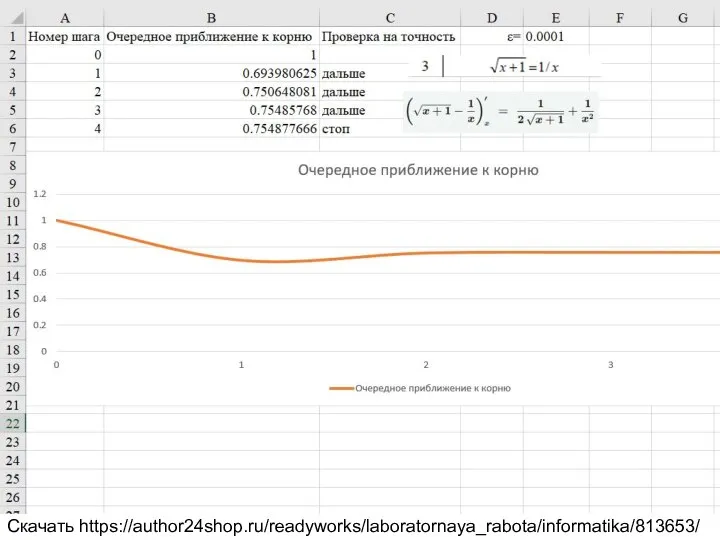
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 3.
√x+1=1/x
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813653/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
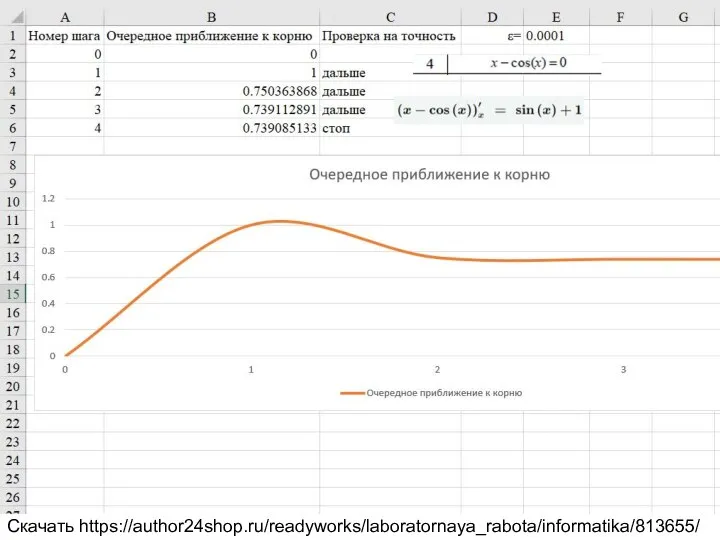
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 4.
x-cos(x)=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813655/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
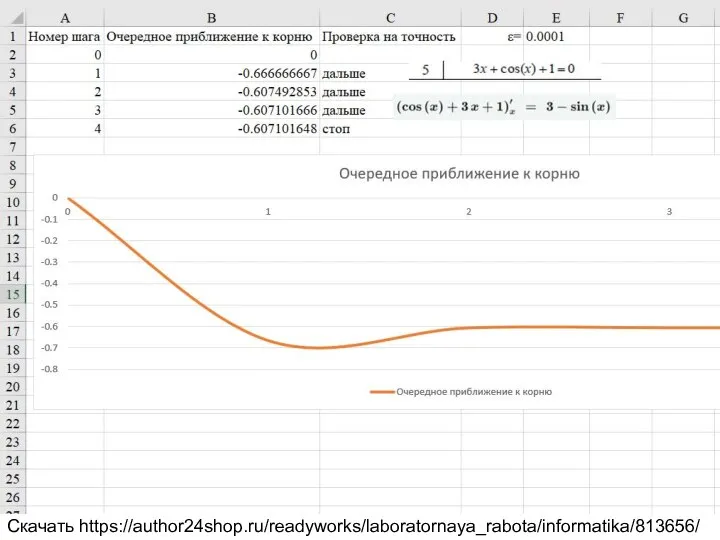
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 5.
3x+cos(x)+1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813656/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
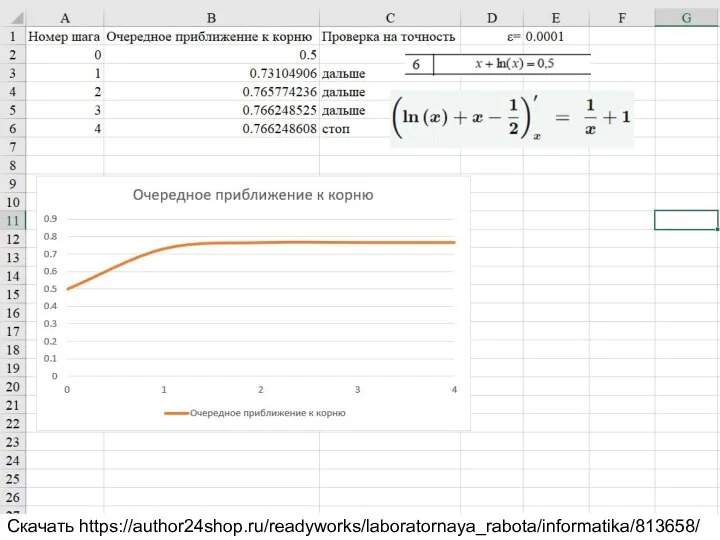
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 6.
x+ln(x)=0.5
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813658/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
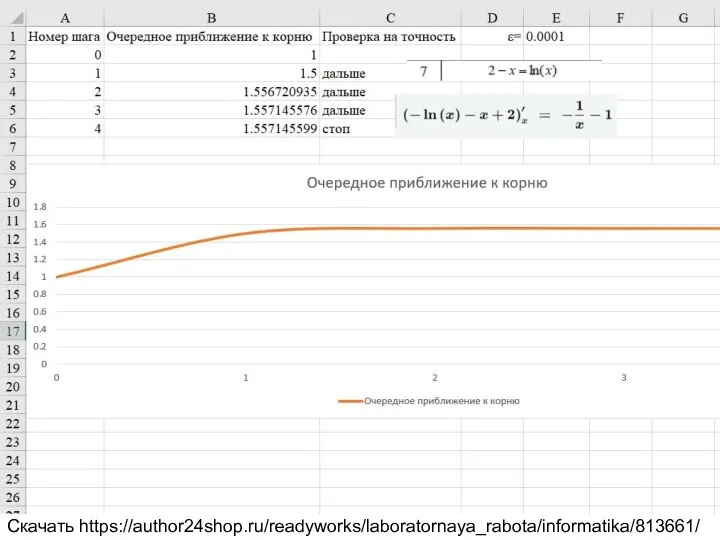
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 7.
2-x=ln(x)
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813661/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
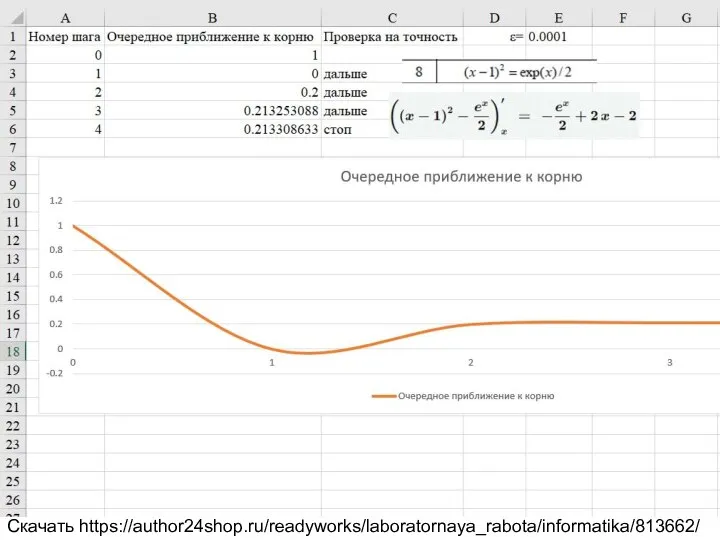
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 8.
(x-1)^2=exp(x)/2
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813662/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
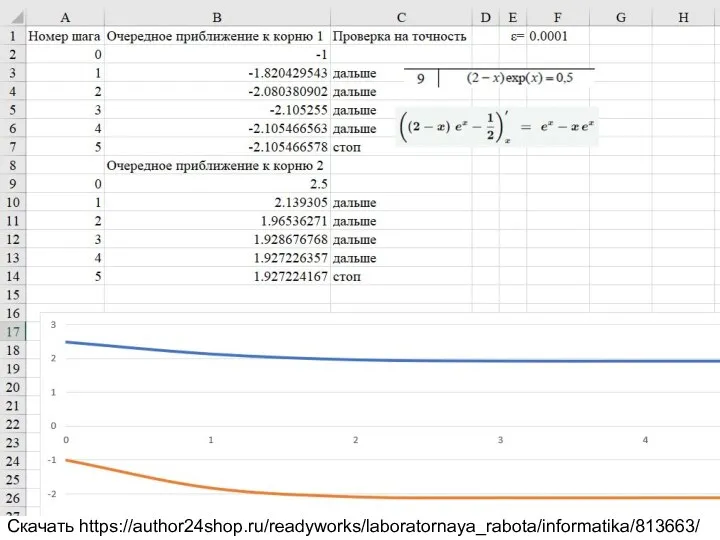
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 9.
(2-x)exp(x)=0.5
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813663/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 10.
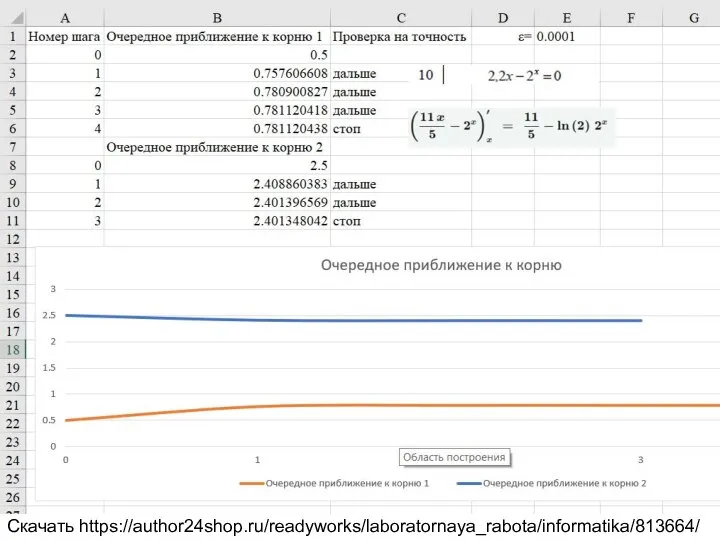
2.2x-2^x=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813664/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 11.
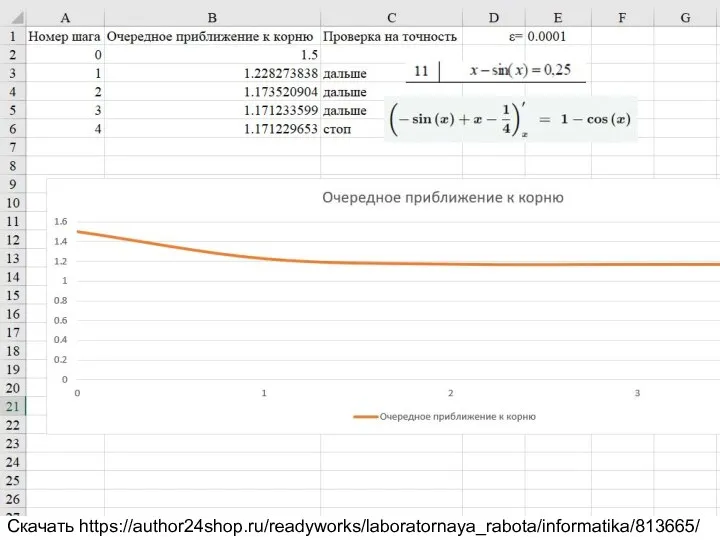
x-sin(x)=0.25
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813665/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 12.
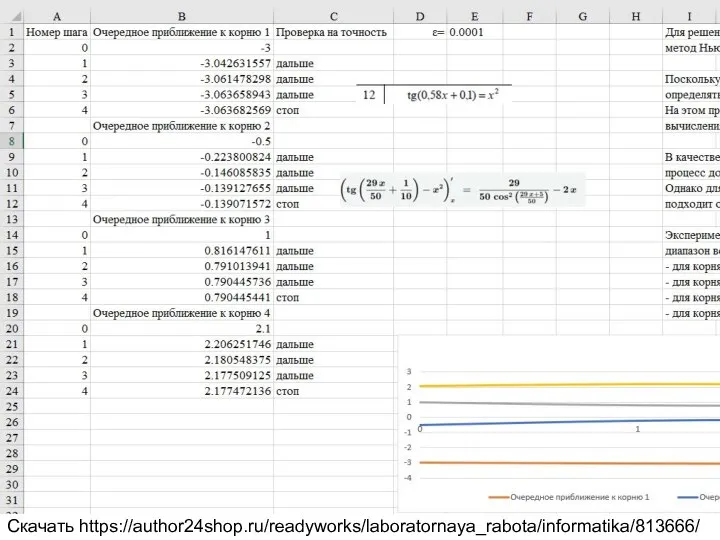
tg(0.58x+0.1)=x^2
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813666/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 13.
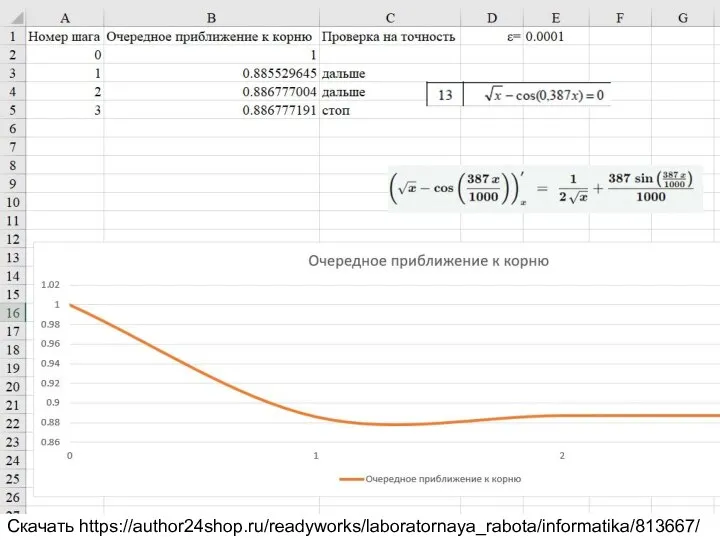
√x-cos(0.387x)=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813667/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 14.
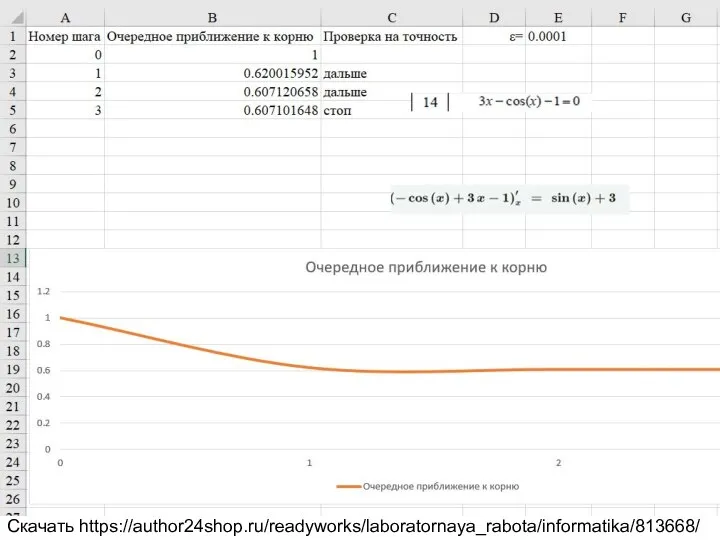
3x-cos(x)-1=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813668/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 15.
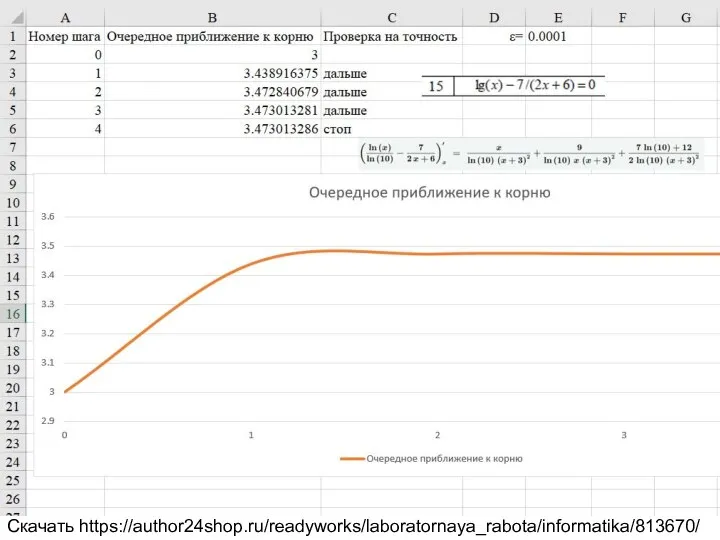
lg(x)-7/(2x+6)=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813670/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 16.
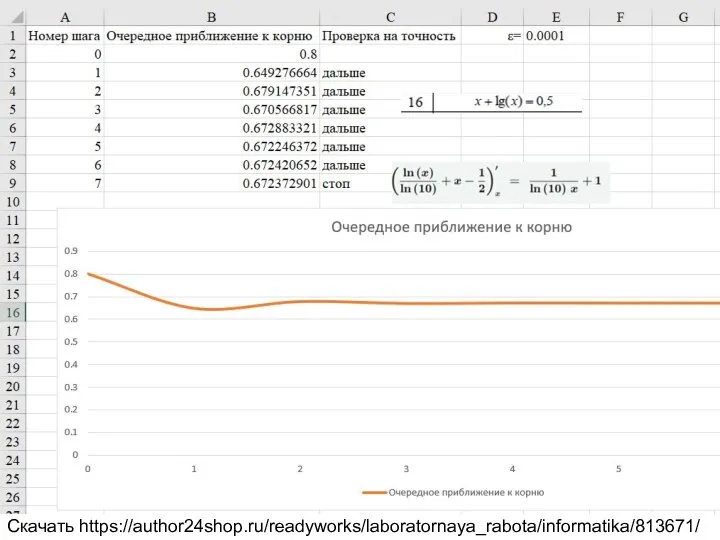
x+lg(x)=0.5
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813671/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 17.
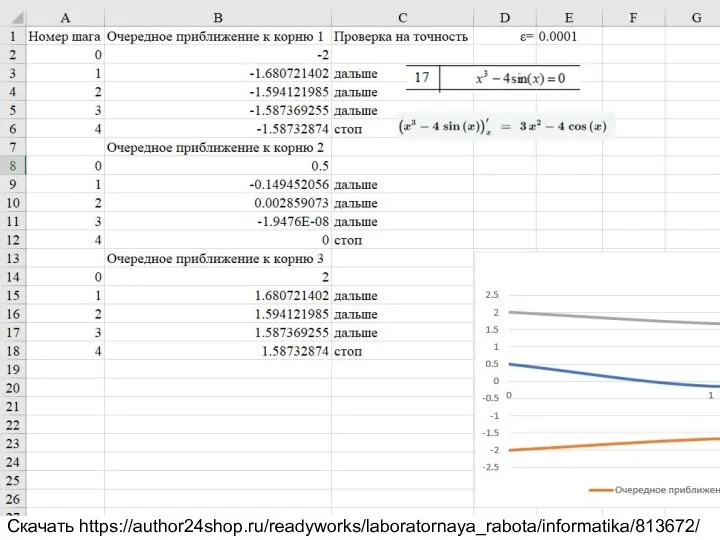
x^3-4sin(x)=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813672/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
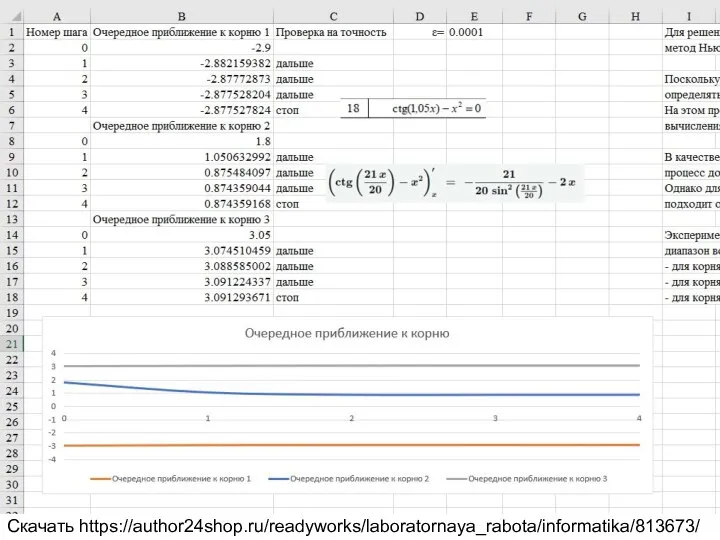
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 18.
ctg(1.05x)-x^2=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813673/
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
2.2.1 Решение нелинейного уравнения методом итерации
Пусть дано уравнение f(x)=0. Для нахождения
xk+1=F(xk), (2.2)
с помощью которой строится итерационный процесс уточнения корней, начиная с начального значения x0, выбираемого самостоятельно. Достаточное условие сходимости процесса: в окрестности корня |F’(x)|<1.
Если процесс расходится (получающиеся приближения удаляются друг от друга) или сходится очень медленно, то необходимо сменить вид представления x=F(x). В этом может оказать помощь другой итерационный метод решения нелинейных уравнений — метод Ньютона. Его итерационная схема имеет вид
xk+1=xk-f(xk)/f’(xk). (2.3)
Сравнивая формулы (2.2) и (2.3), замечаем, что в качестве функции F(xk) можно взять правую часть из формулы (2.3). В большинстве случаев метод Ньютона сходится быстрее.
Задание 2.2. Метод итерации
Решить нелинейное уравнение методом итераций.
Порядок действий в Excel может быть следующий.
1. Представить данное уравнение в виде x=F(x) , взяв его из табл. 2.2. Задать точность решения ε = 0,0001.
2. Создать таблицу с заголовками столбцов Номер шага, Очередное приближение к корню, Проверка на точность.
3. В первую ячейку первой строки таблицы занести значение 0, во вторую — начальное приближение.
4. В следующие строки занести соответственно номер очередного шага, итерационную формулу, вычисляющую правую часть итерационной схемы, и условную формулу, позволяющую помещать в ячейку текст «Стоп» или «Дальше» в зависимости от выполнения заданной точности решения (см. п. 5 алгоритма).
5. Процесс копирования формулы продолжать до получения необходимой точности: разность двух рядом стоящих приближений по модулю должна быть меньше заданного значения ε.
6. После получения решения построить график, иллюстрирующий процесс сходимости: по оси абсцисс отложить номер шага, по оси ординат — очередное приближение к корню.
7. Ответить на вопрос: любое ли начальное приближение можно задавать в вашем варианте? Определить (примерно) диапазон возможных начальных значений, проведя численный эксперимент.
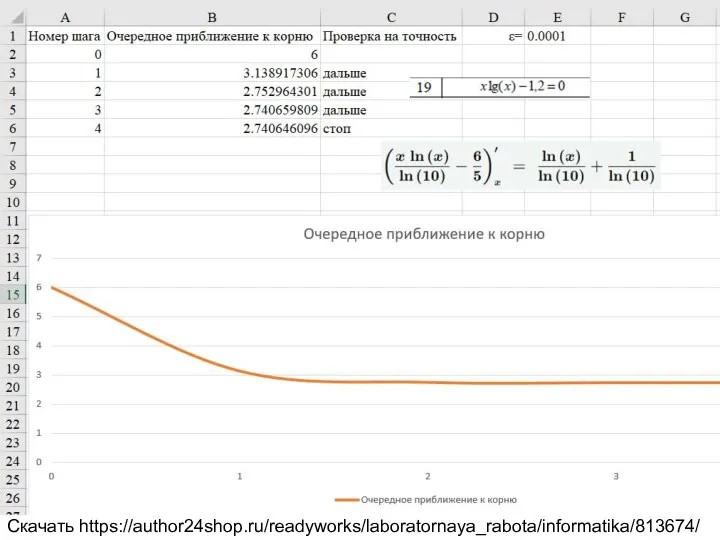
2.2.1 Решение нелинейного уравнения методом итерации. Таблица 2.2 вариант 19.
xlg(x)-1.2=0
Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/813674/
 Десятичные дроби
Десятичные дроби Подготовка к ЕГЭ. Задачи на совместную работу - 2
Подготовка к ЕГЭ. Задачи на совместную работу - 2 Теория систем. Система. Классификация систем. (Тема 3)
Теория систем. Система. Классификация систем. (Тема 3) كتاب رياضيات و كاربرد آن در مديريت
كتاب رياضيات و كاربرد آن در مديريت Кто хочет получить «5»? Игра. Действия с десятичными дробями
Кто хочет получить «5»? Игра. Действия с десятичными дробями Число или цифра 8
Число или цифра 8 Математические модели
Математические модели Интерактивная раскраска. Математическая игра для детей
Интерактивная раскраска. Математическая игра для детей Задачи на готовых чертежах. Признаки равенства треугольников
Задачи на готовых чертежах. Признаки равенства треугольников Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Тренировочная работа № 30
Тренировочная работа № 30 Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Презентация по математике "двузначные числа" - скачать бесплатно
Презентация по математике "двузначные числа" - скачать бесплатно Экономические системы, методы их исследования и моделирования
Экономические системы, методы их исследования и моделирования Самостоятельная работа
Самостоятельная работа Урок математики в 5 классе Автор: Шангина Ирина Евгеньевна, учитель математики ГБОУ СОШ № 11 имени Героя Советского Союза Аипов
Урок математики в 5 классе Автор: Шангина Ирина Евгеньевна, учитель математики ГБОУ СОШ № 11 имени Героя Советского Союза Аипов Подготовка к ЕГЭ по математике. Решение задач В12
Подготовка к ЕГЭ по математике. Решение задач В12 Соотношения между сторонами и углами в прямоугольном треугольнике (задачи на готовых чертежах)
Соотношения между сторонами и углами в прямоугольном треугольнике (задачи на готовых чертежах) Площадь криволинейной трапеции. Определенный интеграл
Площадь криволинейной трапеции. Определенный интеграл Презентация на тему Вычитание натуральных чисел 5 класс
Презентация на тему Вычитание натуральных чисел 5 класс  Раскрытие скобок. 6 класс
Раскрытие скобок. 6 класс Двугранный угол (Урок геометрии в 10 классе)
Двугранный угол (Урок геометрии в 10 классе) Центральная симметрия
Центральная симметрия Функциональные уравнения в школьном курсе математики
Функциональные уравнения в школьном курсе математики Объемы и поверхности многогранников
Объемы и поверхности многогранников Увеличение (уменьшение) числа в 10, 100, 1000 раз (4 класс)
Увеличение (уменьшение) числа в 10, 100, 1000 раз (4 класс) Проект по геометрии на тему: Формулы площадей треугольников
Проект по геометрии на тему: Формулы площадей треугольников Поле чудес
Поле чудес