Содержание
- 2. Алгоритм 1. Разложить левую часть уравнения на множители. - вынесение за скобки общего множителя; - формулы
- 3. Уравнения, решаемые методом разложения на множители. Вынести за скобки общий множитель Пример 1 х³ – 9х
- 4. Пример 2 а³ - 2 – а + 2а² = 0 Применим способ группировки (а³ -
- 5. Пример 3 х³- 2х² - 5х + 6 = 0 Применить алгоритм деления многочлена на многочлен
- 6. Вынесение за скобки общего множителя Алгоритм - найти общий множитель; - вынести его за скобки. Пример:
- 7. Формулы сокращенного умножения 1. Формула разности квадратов а² – в² = (а – в) (а +
- 8. Способ группировки применяется к многочленам, которые не имеют общего множителя для всех членов многочлена. Алгоритм 1.
- 9. Алгоритм 3. Найти целый корень многочлена Рп-1(х), если такой есть. (аналогично п.1) Рп-1(х) : (х –
- 10. Пример: Р3(х) = х³- 2х² - 5х + 6 6 делится на -1; 1; -2; 2;
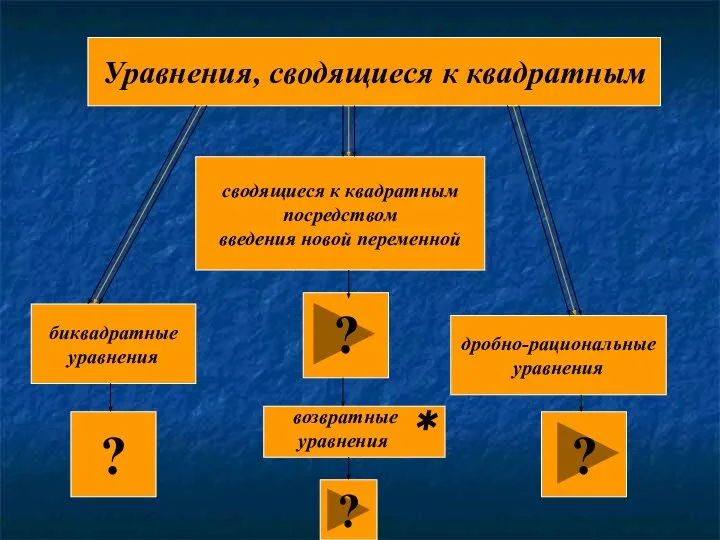
- 11. Уравнения, сводящиеся к квадратным биквадратные уравнения сводящиеся к квадратным посредством введения новой переменной дробно-рациональные уравнения ?
- 12. Биквадратными уравнениями ах4 + вх² + с = 0, где а ≠ 0. называют уравнения вида
- 13. Пример. 4х 4- 5х² + 1 = 0 Заменим х на t ² Пусть х 2
- 14. Уравнения, сводящиеся к квадратным посредством введения новой переменной (ax² + bx)² – c (ax² + bx)
- 15. Пример (х² + 2 х + 4)²– 7 ( х² + 2 х + 4) +
- 16. Возвратные уравнения ax4 + bx³+ cx² + dx + m = 0 от произвольного уравнения четвертой
- 17. Алгоритм 1. Так как , обозначим , тогда 2. Уравнение примет вид. аx 4 + bx³+
- 18. Пример: x 4 + 2x³ - 18x² - 10x + 25 = 0 Объединим I и
- 19. Дробно – рациональные уравнения уравнения вида Р1 (х) Q1 (x) Р 3(х) Q3 (x) Р2 (х)
- 20. Алгоритм 1. Найти общий знаменатель дробей, входящих в уравнение. 2. Умножить обе части уравнения на общий
- 22. Скачать презентацию


















 Декартовы прямоугольные координаты. Действия над векторами заданными своими координатами
Декартовы прямоугольные координаты. Действия над векторами заданными своими координатами Сходимость последовательности СВ
Сходимость последовательности СВ Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Презентация по математике "Числовой луч 3 класс" - скачать
Презентация по математике "Числовой луч 3 класс" - скачать  Примеры на действия с алгебраическими дробями
Примеры на действия с алгебраическими дробями Вычисления с радикалами и степенями
Вычисления с радикалами и степенями Действия с десятичными дробями в коррекционной школе. 8 класс
Действия с десятичными дробями в коррекционной школе. 8 класс Прямоугольные треугольники. Свойства прямоугольных треугольников. Решение задач
Прямоугольные треугольники. Свойства прямоугольных треугольников. Решение задач Финансовая математика: банки, вклады, кредиты
Финансовая математика: банки, вклады, кредиты Сложение рациональных чисел
Сложение рациональных чисел Производная функции
Производная функции Федеральный государственный стандарт основного общего образования : от идеи до внедрения
Федеральный государственный стандарт основного общего образования : от идеи до внедрения Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Устный счёт в пределах 10
Устный счёт в пределах 10 Зачетная система подготовки учащихся к выпускному экзамену по математике в форме ГИА
Зачетная система подготовки учащихся к выпускному экзамену по математике в форме ГИА Специальные кривые
Специальные кривые Элементы теории вероятностей
Элементы теории вероятностей Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Случайные погрешности
Случайные погрешности Десятки и единицы
Десятки и единицы Свойства параллелограмма
Свойства параллелограмма Тренажер Домики. Состав числа в пределах 10
Тренажер Домики. Состав числа в пределах 10 Сложение однозначных чисел с переходом через десяток вида + 8, + 9
Сложение однозначных чисел с переходом через десяток вида + 8, + 9 Кездейсоқ шамалар және олардың берілу тәсілдері
Кездейсоқ шамалар және олардың берілу тәсілдері Диаметр окружности
Диаметр окружности Арксинус. Решение уравнения Sin t = a
Арксинус. Решение уравнения Sin t = a Оптимизация элементов треугольника при решении задачи «Как поспорили Иван Иванович с Иваном Никифоровичем»
Оптимизация элементов треугольника при решении задачи «Как поспорили Иван Иванович с Иваном Никифоровичем» Приведение дробей к новому знаменателю
Приведение дробей к новому знаменателю