Содержание
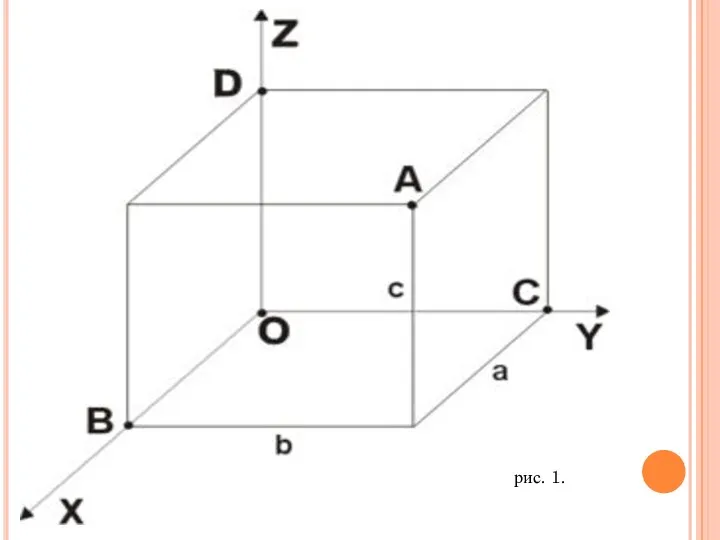
- 2. Декартовы прямоугольные координаты. Декартова прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX,
- 3. рис. 1.
- 4. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой
- 5. Векторы единичной длины i, k , j , направленные вдоль координатных осей, называются координатными ортами. Их
- 6. Радиус вектор Радиус-вектор – это вектор, проведенный из начала координат в точку, где находится тело (рис.
- 7. Действия над векторами заданными своими координатами. при сложении двух и большего числа векторов их одноименные координаты
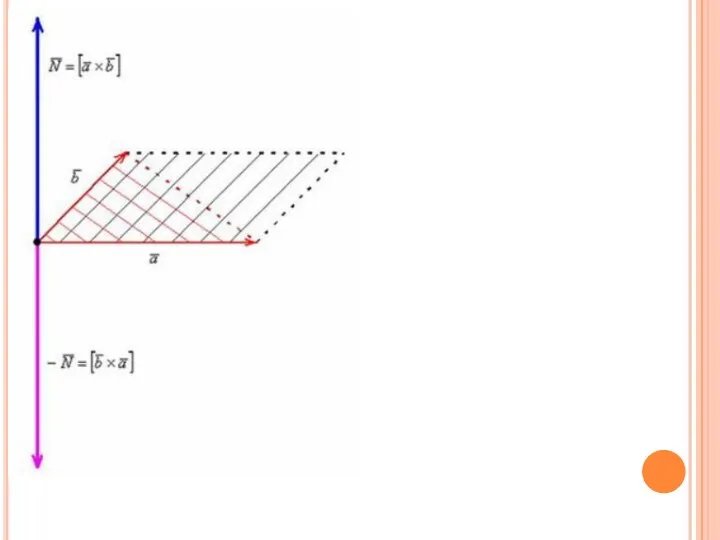
- 8. Векторное произведение векторов. Прямым отличием от скалярного произведения является результат: Векторным произведением неколлинеарных векторов , взятых
- 10. Скалярное произведение векторов. Скалярным произведением двух ненулевых векторов a и b и называется число, равное произведению
- 11. Используемые источники http://allrefs.net/c23/3xg48/p1/ http://www.mathprofi.ru/skaljarnoe_proizvedenie_vektorov.html https://yandex.ru/images/ http://www.mathprofi.ru/vektornoe_proizvedenie_vektorov_smeshannoe_proizvedenie.html http://studopedia.ru/5_66359_dekartova-pryamougolnaya-sistema-koordinat.html http://studopedia.ru/12_58213_deystviya-nad-vektorami-zadannimi-svoimi-koordinatami.html http://life-prog.ru/2_80965_deystviya-s-vektorami-zadannimi-svoimi-koordinatami.html
- 13. Скачать презентацию








 Презентация ученицы 549 школы 6 класса «А» Симоновой Наташи
Презентация ученицы 549 школы 6 класса «А» Симоновой Наташи  Формулы приведения. Математический диктант
Формулы приведения. Математический диктант Натуральные числа и шкалы
Натуральные числа и шкалы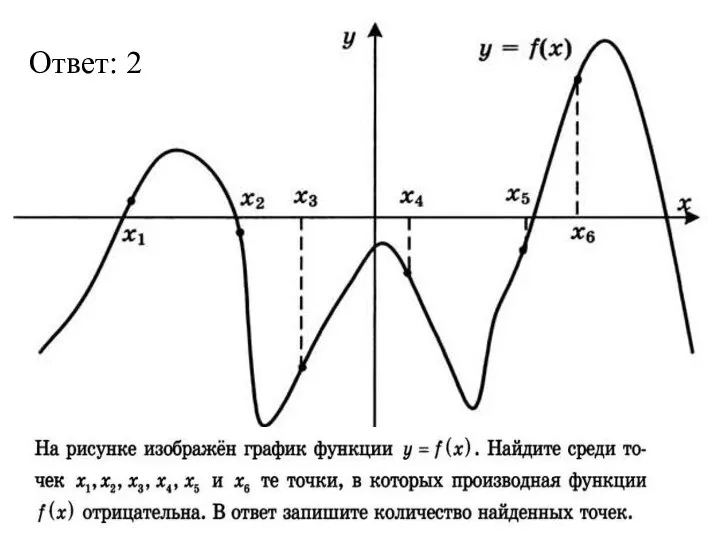 График функции
График функции Задачи на переливание
Задачи на переливание Весёлый счёт
Весёлый счёт Умножение и деление рациональных чисел
Умножение и деление рациональных чисел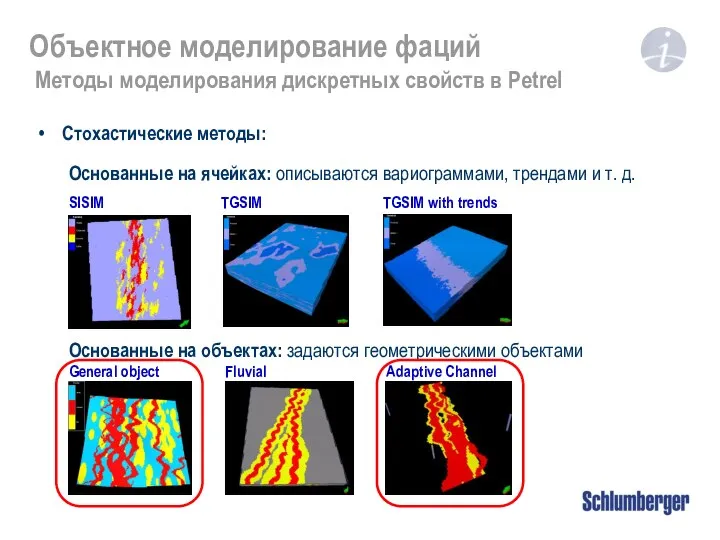 Объектное моделирование фаций. Методы моделирования дискретных свойств в Petrel
Объектное моделирование фаций. Методы моделирования дискретных свойств в Petrel Tomat. Курс ЭМШ
Tomat. Курс ЭМШ Правильные многоугольники. Метапредмет – знание
Правильные многоугольники. Метапредмет – знание Графический метод решения системы уравнений с двумя переменными
Графический метод решения системы уравнений с двумя переменными Геометрическая прогрессия
Геометрическая прогрессия Программирование графики
Программирование графики Взаимно обратные числа
Взаимно обратные числа Открытый урок по математике в 6 классе
Открытый урок по математике в 6 классе Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс) Система координат
Система координат Геометрические места точек. 9 класс
Геометрические места точек. 9 класс Признаки параллельности прямых. Решение задач на готовых чертежах
Признаки параллельности прямых. Решение задач на готовых чертежах Решение задач на составление линейных алгоритмов
Решение задач на составление линейных алгоритмов Формула площади прямоугольника и квадрата
Формула площади прямоугольника и квадрата Графы и их представление на ЭВМ
Графы и их представление на ЭВМ Модуль числа. 6 класс
Модуль числа. 6 класс Треугольник
Треугольник Погрешность и точность приближения. Абсолютная и относительная погрешности
Погрешность и точность приближения. Абсолютная и относительная погрешности Решение задач
Решение задач Урок математики в 4 классе
Урок математики в 4 классе  Аттестационная работа. Образовательная программа элективного курса по математике За страницами учебника
Аттестационная работа. Образовательная программа элективного курса по математике За страницами учебника