Содержание
- 2. Геометрическое изображение комплексных чисел Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости xOy такой, что
- 3. Часто вместо точек на плоскости берут их радиус-векторы т.е. векторы, началом которых служит точка O(0;0), концом
- 4. Формы записи комплексных чисел Запись числа в виде z=x+iy называют алгебраической формой комплексного числа. Из рисунка
- 5. При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного
- 6. Решение. Комплексное число z=x+iy в тригонометрической форме имеет вид z=r(cosφ +isinφ), где 1) z1=1+i (число z1
- 7. Действия над комплексными числами, заданными в тригонометрической форме Рассмотрим два комплексных числа z1 и z2 ,
- 8. б) Частное двух комплексных чисел Пусть заданы комплексные числа z1 и z2 ≠ 0. Рассмотрим частное
- 9. Пример 5. Даны два комплексных числа Найдите Решение. 1) Используя формулу . получаем Следовательно, 2) Используя
- 10. в) Возведение комплексного числа, заданного в тригонометрической форме в n-ю степень Из операции умножения комплексных чисел
- 11. Заслуги Муавра: открыл (1707) формулу Муавра для возведения в степень (и извлечения корней) комплексных чисел, заданных
- 12. г) Извлечение корня п-ой степени из комплексного числа Корнем п-ой степени из комплексного числа z называется
- 13. Таким образом, извлечение корня n-ой степени из комплексного числа z всегда возможно и дает n различных
- 14. Запишем все значения : при при при Ответ:
- 15. Вопросы для самоконтроля 1. Сформулируйте определение комплексного числа. 2. Какое комплексное число называется чисто мнимым? 3.
- 17. Скачать презентацию














 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Построение графика функции
Построение графика функции Полиномы от нескольких переменных. Нахождение НОД. (Лекция 5.1)
Полиномы от нескольких переменных. Нахождение НОД. (Лекция 5.1) Решение уравнений. Равенства
Решение уравнений. Равенства 1-ден 10 дейінгі сандар
1-ден 10 дейінгі сандар ЕГЭ. Базовый уровень. Действия с дробями
ЕГЭ. Базовый уровень. Действия с дробями Углы и отрезки, связанные с окружностью. 10 класс
Углы и отрезки, связанные с окружностью. 10 класс Прямоугольный параллелепипед. Урок по геометрии в 10 классе
Прямоугольный параллелепипед. Урок по геометрии в 10 классе Дробные выражения
Дробные выражения Прямая пропорциональность. 7 класс
Прямая пропорциональность. 7 класс Площадь многоугольников. Теорема Пифагора. Решение задач
Площадь многоугольников. Теорема Пифагора. Решение задач Второй признак подобия треугольников
Второй признак подобия треугольников Весёлая матиматека
Весёлая матиматека ГИА 2014 Задание 17. Подобные треугольники
ГИА 2014 Задание 17. Подобные треугольники Математические задумки-3 3 класс
Математические задумки-3 3 класс Деление чисел
Деление чисел Измерительные работы на местности
Измерительные работы на местности Сумма и произведение вероятностей
Сумма и произведение вероятностей Решение задач с помощью уравнений
Решение задач с помощью уравнений Построение графика функции y = f (x)+m, если известен график функции y = f (x)
Построение графика функции y = f (x)+m, если известен график функции y = f (x) Треугольное королевство. 1 класс
Треугольное королевство. 1 класс Занятие 14. 6 класс.
Занятие 14. 6 класс. Задание № 13. Укажите номера верных утверждений
Задание № 13. Укажите номера верных утверждений Приемы быстрого умножения
Приемы быстрого умножения Математические ребусы
Математические ребусы Графы. Сети. Деревья
Графы. Сети. Деревья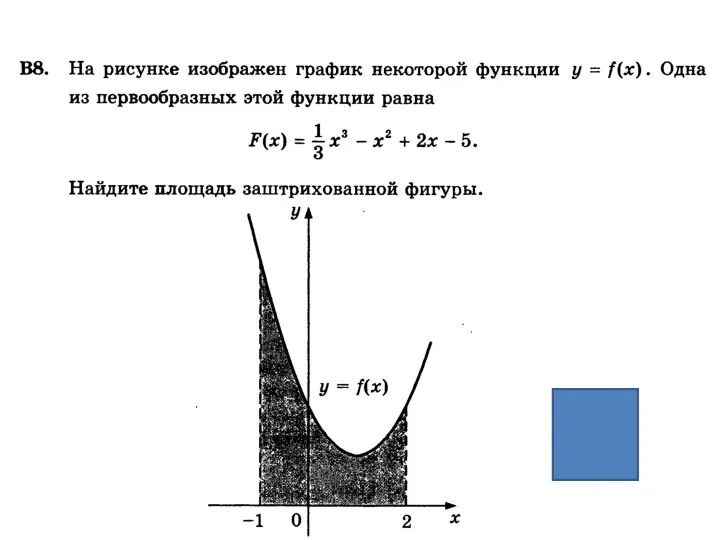 Функции
Функции Информация из оптимальной Симплекс-таблицы
Информация из оптимальной Симплекс-таблицы