Содержание
- 2. №1. Сколько различных решений имеет логическое уравнение: (a ∨ ¬ b) ∧ (b ∨ ¬ c)
- 3. (a ∨ ¬ b) ∧ (b ∨ ¬ c) ∧ (c ∨ ¬ d) ∧ (d
- 4. №2. Сколько существует различных наборов значений логических переменных, которые удовлетворяют всем условиям? (x1 → x2)∧ (x2
- 5. (x1 → x2)∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) = 1
- 6. №4. Сколько существует различных наборов значений логических переменных, которые удовлетворяют перечисленным условиям? (x1 → x2) ∧
- 7. (x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) =
- 8. № 5. Сколько различных решений имеет система уравнений: № 6. Ответ: 11 Решение: (x1 → x2)
- 9. (x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧(x4 → x5) = 1
- 10. Количество решений системы уравнений: 6+6-1=11 (решение, выделенное красным цветом, нужно учесть один раз).
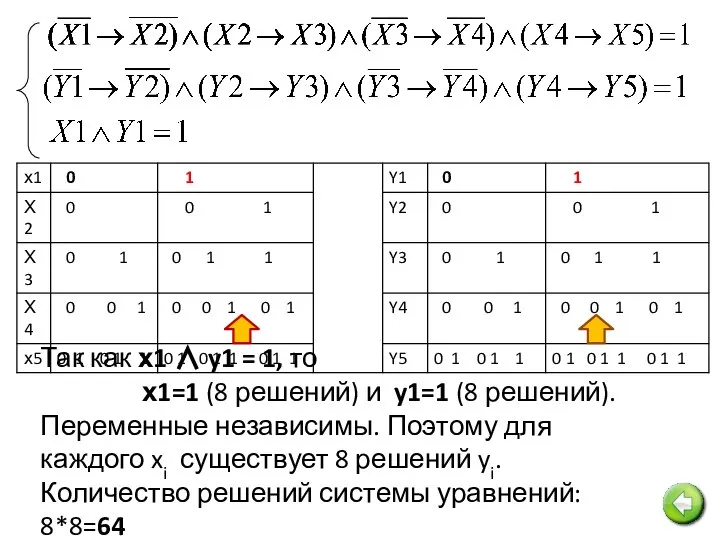
- 11. № 7. Сколько различных решений имеет система логических уравнений: (X1 ∨ X2) ∧ (X2 ∨ X3)
- 12. Так как х1 ∧ y1 = 1, то х1=1 (8 решений) и y1=1 (8 решений). Переменные
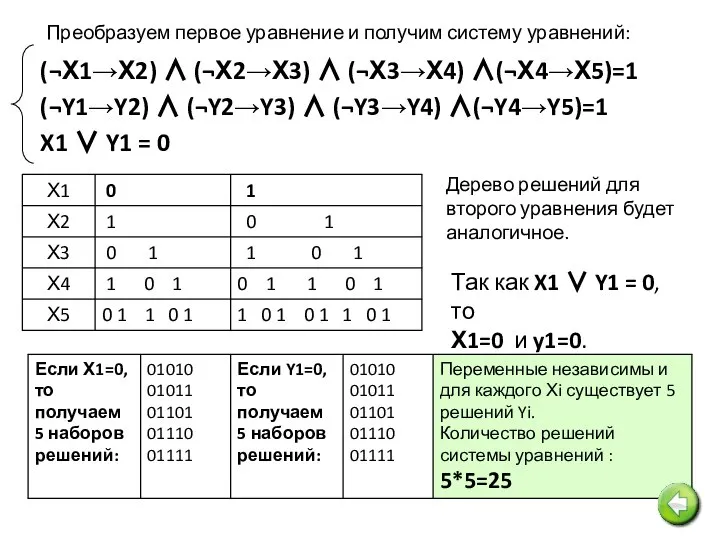
- 13. (¬Х1→Х2) ∧ (¬Х2→Х3) ∧ (¬Х3→Х4) ∧(¬Х4→Х5)=1 (¬Y1→Y2) ∧ (¬Y2→Y3) ∧ (¬Y3→Y4) ∧(¬Y4→Y5)=1 X1 ∨ Y1 =
- 14. Сколько различных решений имеет система логических уравнений: (x1 → x2)∧ (x2 → x3) ∧ (x3 →
- 15. (x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5) =
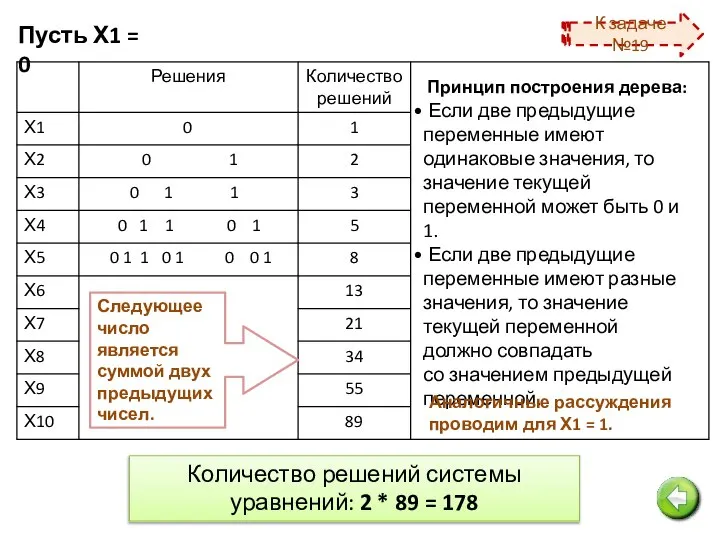
- 16. №11. Сколько различных решений имеет система уравнений: Ответ: Ответ: 178 20 (x1 ≡ x2) ∨ (x1
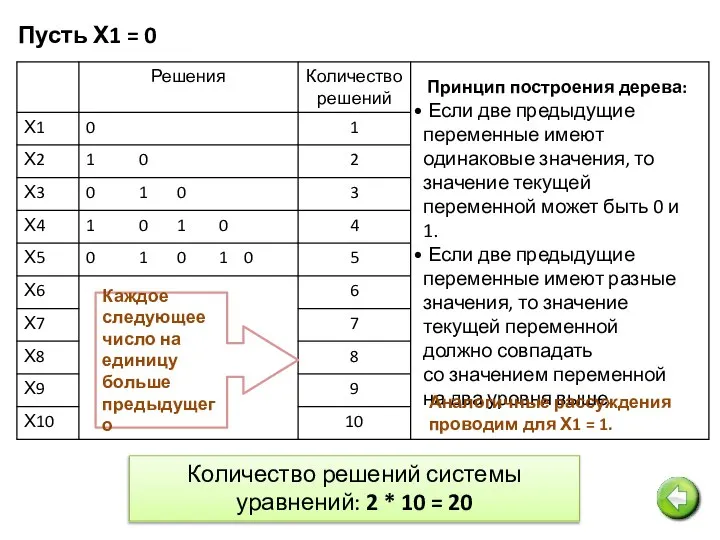
- 17. Пусть Х1 = 0 Принцип построения дерева: Если две предыдущие переменные имеют одинаковые значения, то значение
- 18. Пусть Х1 = 0 Принцип построения дерева: Если две предыдущие переменные имеют одинаковые значения, то значение
- 19. Сколько различных решений имеет система уравнений: Ответ: 18 Решение: (x2 ≡ x1) ∨ (x2 ≡ x3)=1
- 20. Количество решений системы уравнений: 20-2=18 (x2 ≡ x1) ∨ (x2 ≡ x3)=1 (x3 ≡ x1) ∨
- 21. Воспользуемся методом «замены переменных». Введем новые переменные: Х = A → B и Y = C
- 22. №11_d. Сколько различных решений имеет система уравнений: Ответ: 192 Решение:
- 23. Построим дерево решений для новой системы уравнений: Так как Y1 = X1 ≡ X2, то Y1=0
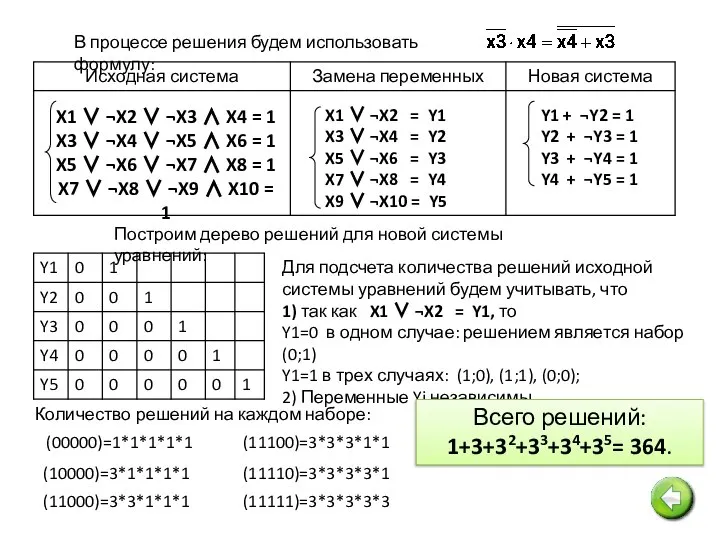
- 24. №12. Сколько различных решений имеет уравнение (система уравнений): Ответ: Ответ: 64 364 №13. Решение: Решение:
- 25. Y1 = (X1 ≡ X2) Y2 = (X3 ≡ X4) Y3 = (X5 ≡ X6) Y4
- 26. В процессе решения будем использовать формулу: Построим дерево решений для новой системы уравнений: Для подсчета количества
- 27. №14. Сколько различных решений имеет система уравнений: Ответ: 64 Решение: ((X1 ≡ X2) + (X3 ≡
- 28. Дерево решений: Так как Yi = (Xi ≡ Xi+1) имеет две пары решений, как для 1,
- 29. №15. Сколько различных решений имеет система уравнений: Ответ: 192 Решение:
- 30. Так как См. решение задачи № 11 d. Так как Yi = (Xi ≡ Xi+1) имеет
- 31. №16. Сколько различных решений имеет система уравнений: Ответ: 224 Решение:
- 32. См. решение задачи № 11 d. Только в нашем случае количество переменных шесть, поэтому ответ: 7*26=448.
- 33. №17. Сколько различных решений имеет система уравнений: Ответ: Ответ: 244 120 A → B ∨ C
- 34. Построим дерево решений для новой системы уравнений: Два решения: (00000) и (11111). Для подсчета количества решений
- 35. A → B ∨ C ∧ ¬D = 1 C → D ∨ E ∧ ¬
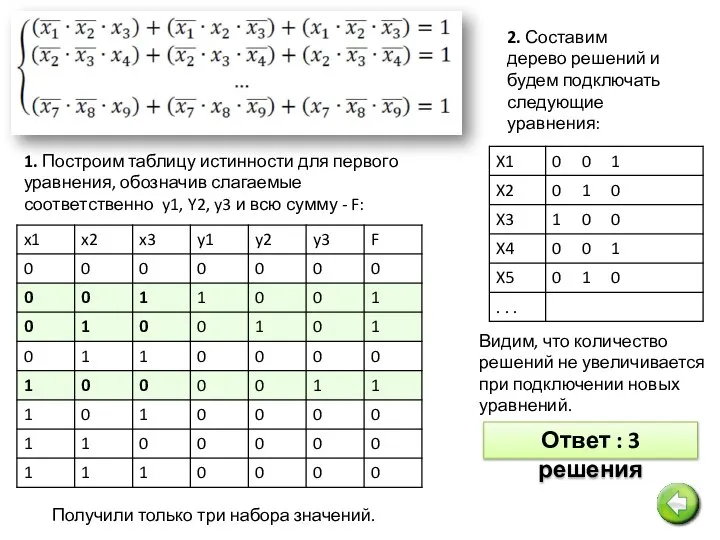
- 36. №18. Сколько различных решений имеет система уравнений: Ответ: 3 Решение:
- 37. 1. Построим таблицу истинности для первого уравнения, обозначив слагаемые соответственно y1, Y2, y3 и всю сумму
- 38. №19. Сколько различных решений имеет система уравнений: Ответ: 110 Решение:
- 39. Так как То исходная система примет вид: См. решение задачи № 11 b. Только в нашем
- 40. №20_А). Сколько различных решений имеет система уравнений: x1 → x2 → x3 → x4 → x5
- 41. Расставим скобки: т.к. все операции имеют одинаковый приоритет, то они выполняются последовательно слева направо. (((x1 →
- 42. №20_Б). Сколько различных решений имеет система уравнений: Ответ: 1387 Решение: x1 → x2 → x3 →
- 43. Рассмотрим x1 → x2. Если х1=0, то получаем два решения: 1 и 1. Если х1=1, то
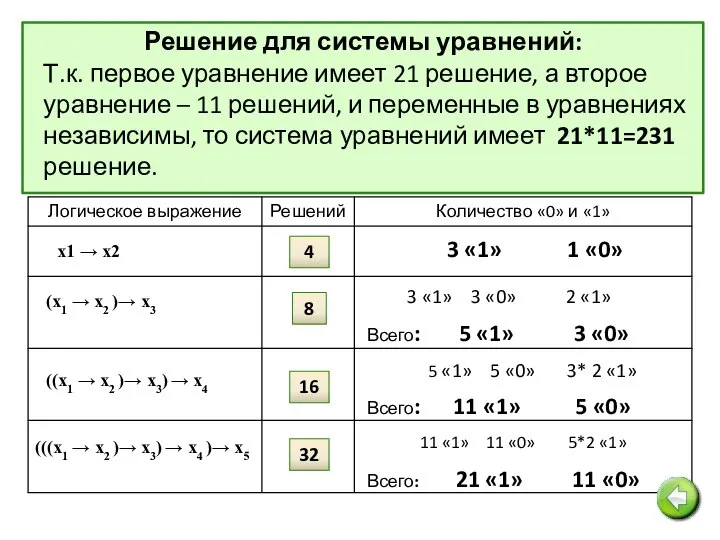
- 44. Решение для системы уравнений: Рассмотрим третье уравнение: x1 → y1 = 1. Если х1=1, то y1=1.
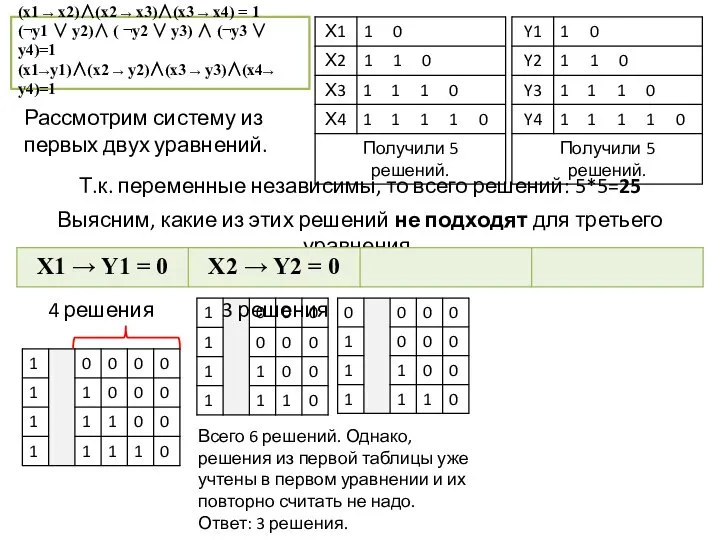
- 45. (x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1 (¬у1 ∨ у2)
- 46. (x1 → x2)∧(x2 → x3)∧(x3 → x4) = 1 (¬у1 ∨ у2)∧ ( ¬у2 ∨ у3)
- 47. (x1 → x2)∧(x2 → x3)∧(x3 → x4) = 1 (¬у1 ∨ у2)∧ ( ¬у2 ∨ у3)
- 48. (x1 → x2)∧(x2 → x3)∧(x3 → x4) = 1 (¬у1 ∨ у2)∧ ( ¬у2 ∨ у3)
- 50. Скачать презентацию







































 Задачі на логіку
Задачі на логіку Геометрия мәселелері
Геометрия мәселелері Презентация на тему Рабочая программа по математике для 5 класса по УМК
Презентация на тему Рабочая программа по математике для 5 класса по УМК Основные типы задач по усвоению общего функционального материала
Основные типы задач по усвоению общего функционального материала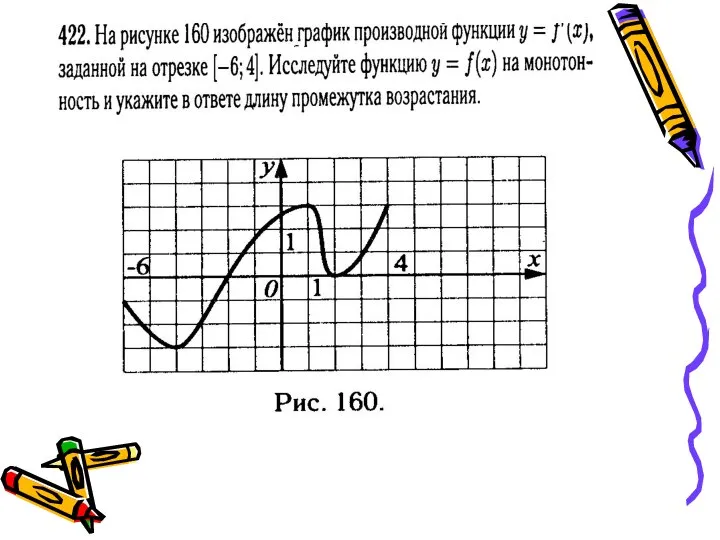 Производная, монотонность, экстремумы
Производная, монотонность, экстремумы Объем пирамиды. Определение. Формулы. Интересные сведения. Задачи
Объем пирамиды. Определение. Формулы. Интересные сведения. Задачи Презентация по математике "Приём вычисления для случаев вида 36 + 2, 36 + 20" - скачать
Презентация по математике "Приём вычисления для случаев вида 36 + 2, 36 + 20" - скачать  Последовательность комплексных чисел
Последовательность комплексных чисел Кто живет под грибом
Кто живет под грибом Возникновение и развитие геометрии
Возникновение и развитие геометрии Оценка прочности и прогнозирование ресурса рабочих колес авиационных ГТД
Оценка прочности и прогнозирование ресурса рабочих колес авиационных ГТД Площадь треугольника. Теоремы, следствия и задачи
Площадь треугольника. Теоремы, следствия и задачи Математика и физика. Интегрированный урок в 9 классе.
Математика и физика. Интегрированный урок в 9 классе. Теорема Фалеса
Теорема Фалеса Космос
Космос Задачи на движение Тема урока: движение в противоположных направлениях
Задачи на движение Тема урока: движение в противоположных направлениях Конус. Определение конуса
Конус. Определение конуса Математическая игра для 5-х классов «Путешествие по стране Математика» Материал подготовила учитель математики
Математическая игра для 5-х классов «Путешествие по стране Математика» Материал подготовила учитель математики  Презентация по математике "Аксиомы стереометрии" - скачать бесплатно
Презентация по математике "Аксиомы стереометрии" - скачать бесплатно Элементы высшей математики. Обратная матрица
Элементы высшей математики. Обратная матрица Устойчивость узла нагрузки
Устойчивость узла нагрузки Статистика. Теория статистики
Статистика. Теория статистики Вероятность и статистика. Система подготовки к ГИА и ЕГЭ
Вероятность и статистика. Система подготовки к ГИА и ЕГЭ Дифференциальные уравнения
Дифференциальные уравнения Задачи на нахождение неизвестного уменьшаемого, неизвестного вычитаемого
Задачи на нахождение неизвестного уменьшаемого, неизвестного вычитаемого Ковалевская Софья Васильевна (1850-1891)
Ковалевская Софья Васильевна (1850-1891) Краткосрочный учебный проект «Цилиндр как фигура вращения» (в рамках «Intel»)
Краткосрочный учебный проект «Цилиндр как фигура вращения» (в рамках «Intel») Прямоугольный треугольник
Прямоугольный треугольник