Содержание
- 2. Уравнения с разделяющимися переменными Наиболее простым ДУ первого порядка является уравнение вида: Такое уравнение называется уравнением
- 3. Уравнения с разделяющимися переменными Получаем: Замечание: при проведении почленного деления ДУ на могут быть потеряны некоторые
- 4. Уравнения с разделяющимися переменными Разделим обе части уравнения на xy: Общий интеграл ДУ Решим уравнение xy
- 5. Уравнения с разделяющимися переменными Рассмотрим задачу, приводящую к ДУ первого порядка с разделяющимися переменными: Задача: материальная
- 6. Уравнения с разделяющимися переменными По условию задачи: Получим дифференциальное уравнение с разделяющимися переменными: Скорость точки изменяется
- 7. ДУ с однородной функцией нулевого порядка в правой части. (однородные уравнения первого порядка).
- 8. Функция f(x;y) называется однородной степени n, если умножение всех её аргументов на одно и то же
- 9. Пример 1. - однородная функция 3-ей степени Так как
- 10. - однородная функция 1-ой степени Так как - однородная функция 0-ой степени Так как
- 11. - однородная функция 2-ой степени Так как - однородная функция (-1)-ой степени Так как
- 12. ДУ I порядка называется однородным, если f(x;y)- однородная функция 0-ой степени, т.е.
- 13. Однородное ДУ I порядка можно записать в виде: Т.к. , то если положить Получаем:
- 14. Решение однородного ДУ I порядка Это уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены
- 15. или
- 16. или -общее решение данного ДУ
- 17. Пример 2. Найти общее решение ДУ: Это однородное ДУ вида ⇒
- 20. Пример 3. Решить задачу Коши: , если y(1)=0 Это однородное ДУ вида ⇒
- 23. - общее решение Решим задачу Коши у(1)=0 : или - частное решение
- 24. Уравнение вида называется однородным уравнением в дифференциальной форме, если M(x;y) и N(x;y) - однородные функции одной
- 25. Пример 4. Найти общее решение ДУ: M(x;y) N(x;y) - однородное уравнение вида
- 26. ⇒
- 27. (*)
- 28. - общее решение
- 29. Это однородное ДУ можно привести к виду
- 30. ⇒ ⇒
- 31. - получили (*)
- 32. Пример 5. Найти общее решение ДУ: M(x;y) N(x;y) - однородное уравнение вида ⇒
- 34. Пример 6. Найти общее решение ДУ: Это однородное ДУ можно привести к виду
- 35. ⇒
- 36. общий интеграл ду
- 37. - общий интеграл или - общий интеграл
- 38. Линейные уравнения первого порядка
- 39. Линейные уравнения первого порядка Линейным дифференциальным уравнением первого порядка называется ДУ 1-го порядка, линейное относительно неизвестной
- 40. y ′ + p(x) y = 0 Разделим переменные: dx dy + p( x) y =
- 41. Рассмотрим линейное неоднородное уравнение: (1) y ′ + p(x) ⋅ y = f(x) . Существуют два
- 42. y = C( x) ⋅ e−∫ p( x)dx ⇒ dx dx dy = dC ⋅ e−∫
- 43. Таким образом, общее решение линейного неоднородного уравнения (1) имеет вид: (3) (4) Заметим, что первое слагаемое
- 44. II) Метод Бернулли. Будем искать решение (1) в следующем виде: y = u(x) ⋅ v(x) .
- 46. Скачать презентацию













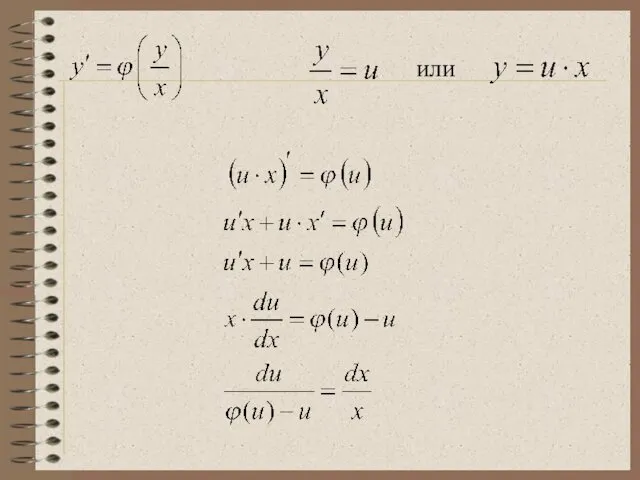


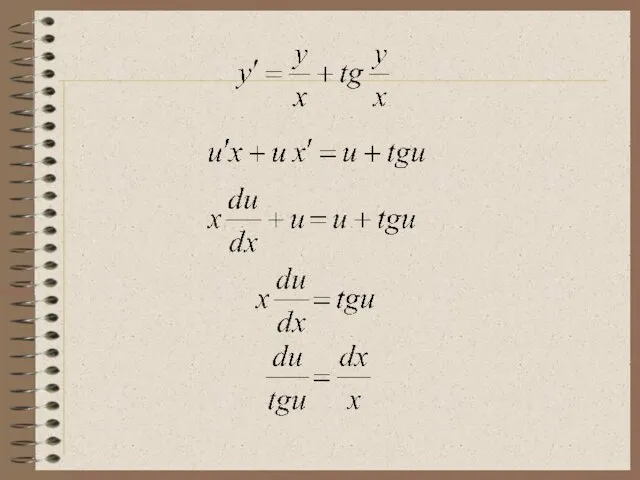
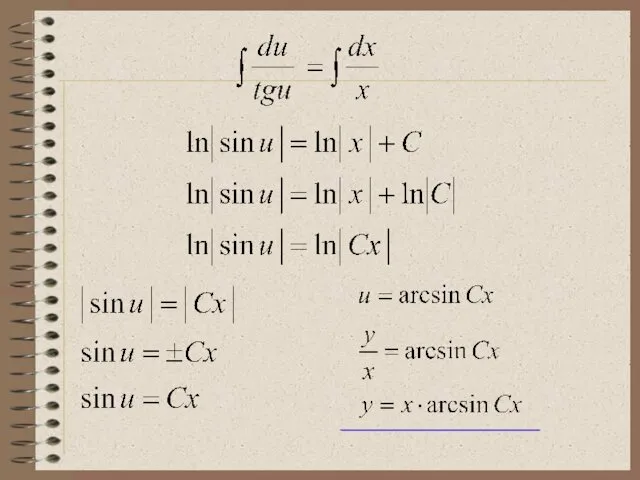

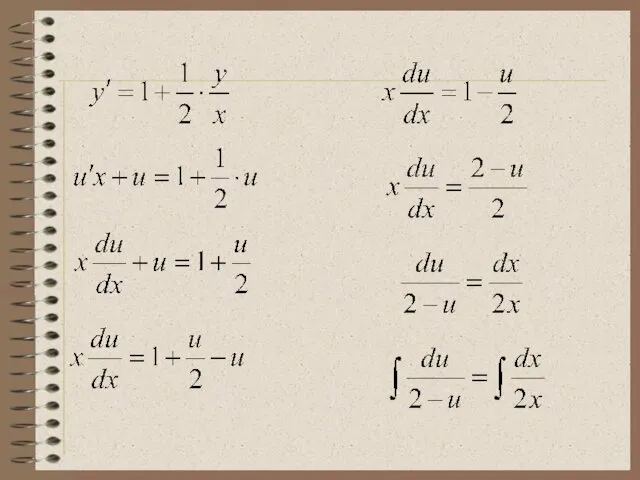




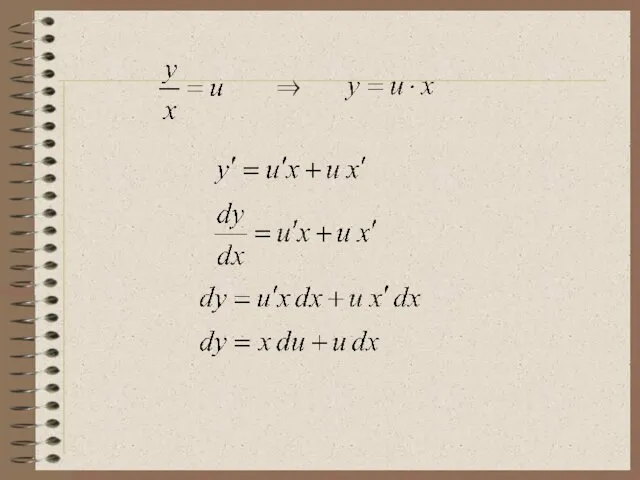
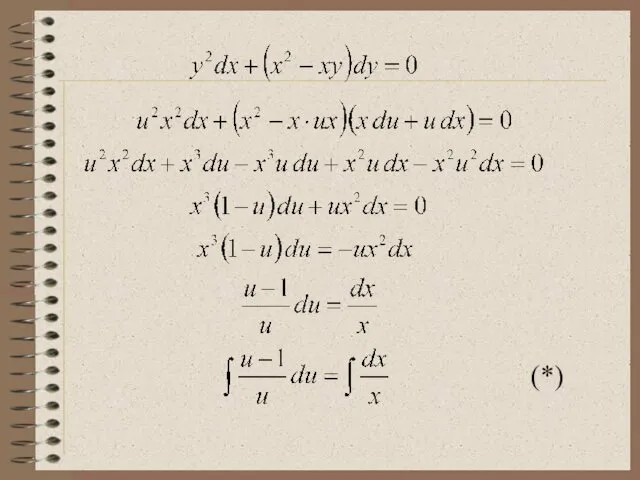


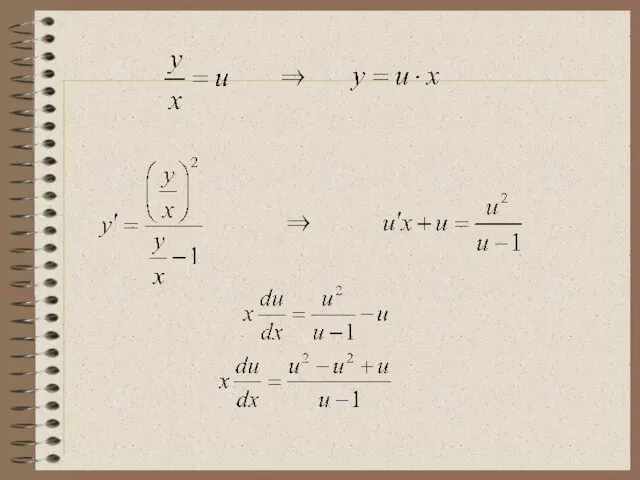




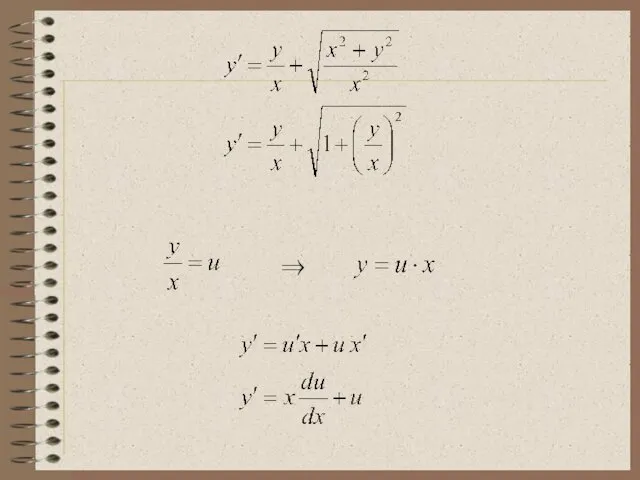









 Решение дробных рациональных уравнений
Решение дробных рациональных уравнений Одночлены 7 класс Бралгина Наталья Михайловна МАОУ СОШ п.Демянск 2011-2012 уч.год
Одночлены 7 класс Бралгина Наталья Михайловна МАОУ СОШ п.Демянск 2011-2012 уч.год  Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Математика - царица наук
Математика - царица наук Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости МОУ СОШ № 37 г. Архангельска МОУ СОШ № 37 г. Архангельска Организация работы математического кружка «Эврика» Садовина В. Е.,
МОУ СОШ № 37 г. Архангельска МОУ СОШ № 37 г. Архангельска Организация работы математического кружка «Эврика» Садовина В. Е.,  МЕТОД КООРДИНАТ «Лучше один раз увидеть, чем сто раз услышать», гласит народная мудрость.
МЕТОД КООРДИНАТ «Лучше один раз увидеть, чем сто раз услышать», гласит народная мудрость.  Презентация по математике "Развитие математики в Древнем Китае" - скачать
Презентация по математике "Развитие математики в Древнем Китае" - скачать  Преобразования графиков функций
Преобразования графиков функций Площадь криволинейной трапеции и интеграл.
Площадь криволинейной трапеции и интеграл.  Понятие объема. Объем прямоугольного параллелепипеда
Понятие объема. Объем прямоугольного параллелепипеда Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Арифметическая прогрессия
Арифметическая прогрессия Презентация на тему Уравнение и его корни 7 класс
Презентация на тему Уравнение и его корни 7 класс Игра «Кто хочет стать математиком»
Игра «Кто хочет стать математиком» Пирамида. Красота пирамиды
Пирамида. Красота пирамиды Деление на 0,1; 0,01
Деление на 0,1; 0,01 Математика и медицина
Математика и медицина Шкалы и координаты
Шкалы и координаты Угол. Прямой и развёрнутый угол. Чертёжный треугольник
Угол. Прямой и развёрнутый угол. Чертёжный треугольник Как измерить высоту дерева при помощи своего роста
Как измерить высоту дерева при помощи своего роста Преобразование графиков функций
Преобразование графиков функций Реализация алгоритма ветвления на QBASIC. Задачи на повторение
Реализация алгоритма ветвления на QBASIC. Задачи на повторение Неполные квадратные уравнения. 8 класс
Неполные квадратные уравнения. 8 класс Свойства корня n-й степени
Свойства корня n-й степени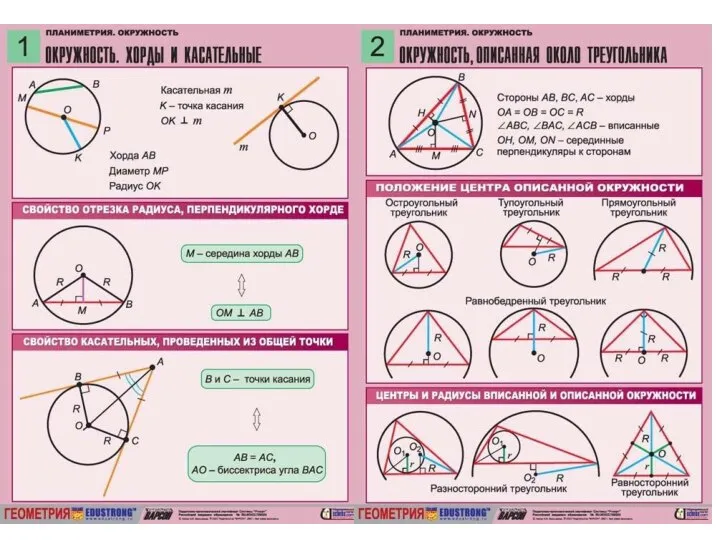 Геометрия. Конспекты
Геометрия. Конспекты Делимость чисел презентация по математике
Делимость чисел презентация по математике Радиус окружности, вписанной в равнобедренный прямоугольный
Радиус окружности, вписанной в равнобедренный прямоугольный