Содержание
- 2. Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы
- 3. ТЕОРЕМА КРАМЕРА Если главный определитель системы линейных алгебраических уравнений Δ отличен от нуля, то эта система
- 4. Формулы Крамера где Δj=0 (j=1,…,n) - определители, образованные из главного определителя СЛУ Δ заменой j-го столбца
- 5. Однородные системы ЛУ (ОСЛУ) Система уравнений с нулевыми свободными членами называется однородной, в противном случае –
- 6. Критерий существования нетривиального решения однородной системы (ОСЛУ) Теорема. Для того, чтобы однородная квадратная система линейных уравнений
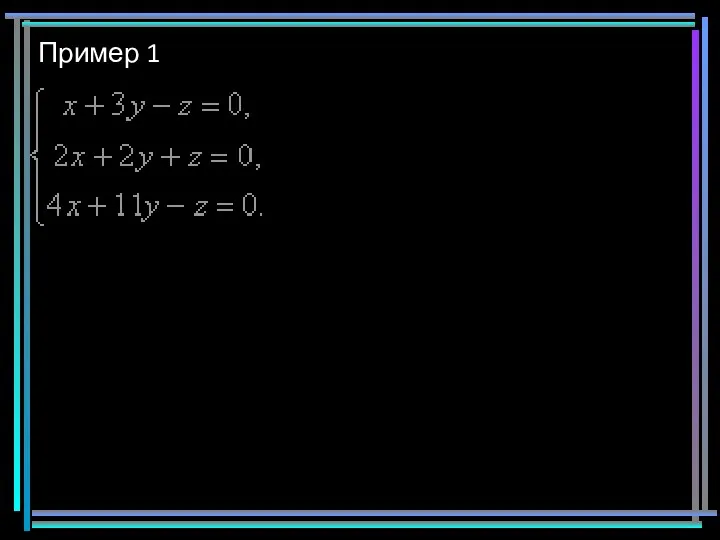
- 7. Пример 1
- 8. Пример 1 Определитель системы не равен нулю, значит ОСЛУ имеет единственное тривиальное решение x=y=z=0. Раскладываем определитель
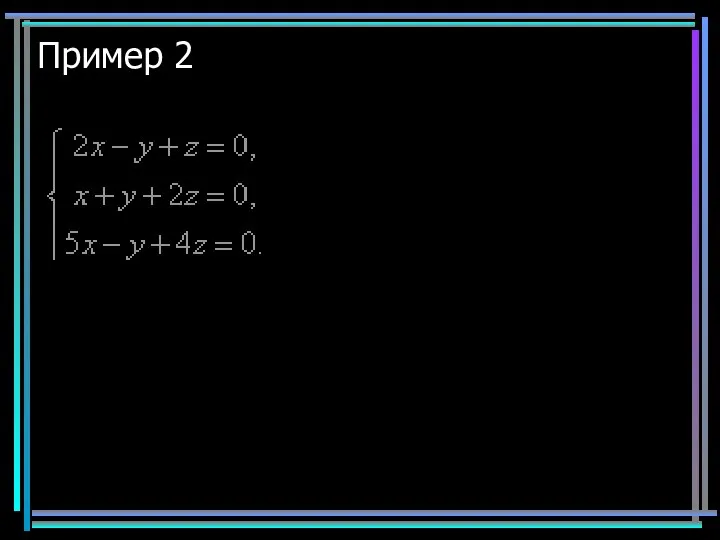
- 9. Пример 2
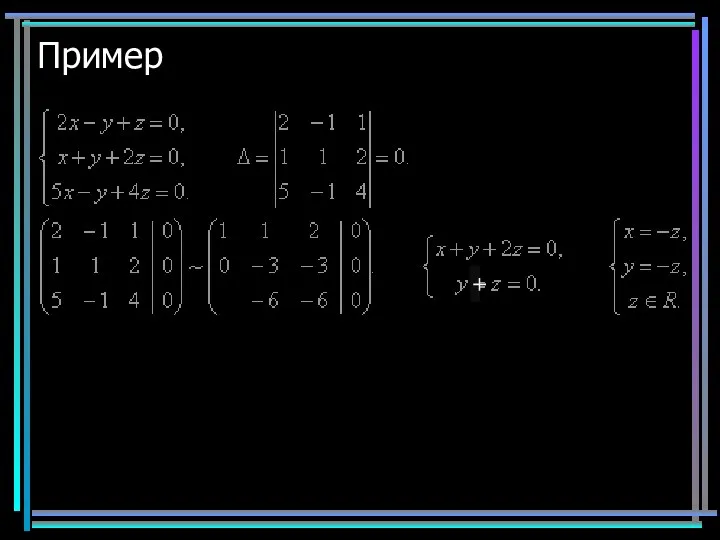
- 10. Пример 2 Бесконечное множество решений
- 11. Пример 2 Ставим 2 строку на место 1-ой, умножаем ее на (-2) и складываем со 2-ой.
- 12. Пример 2 Ставим 2 строку на место 1-ой, умножаем ее на (-2) и складываем со 2-ой.
- 13. Пример +
- 14. Решение систем линейных уравнений матричным методом или методом обратной матрицы
- 15. Обратная матрица Пусть A — квадратная матрица порядка nхn: Если существует квадратная матрица X той же
- 16. Пример
- 17. Невырожденная матрица ― квадратная матрица ― квадратная матрица, определитель ― квадратная матрица, определитель которой отличен от
- 18. Всякая невырожденная матрица A имеет единственную обратную матрицу. Aij — алгебраическое дополнение элемента aij матрицы A.
- 19. Свойства обратной матрицы (справедливы для любых невырожденных матриц): (A·B)−1 = B−1·A−1; (A−1)−1= A; E−1=E; A·A−1·A =
- 20. Пусть задана СЛАУ следующего вида:
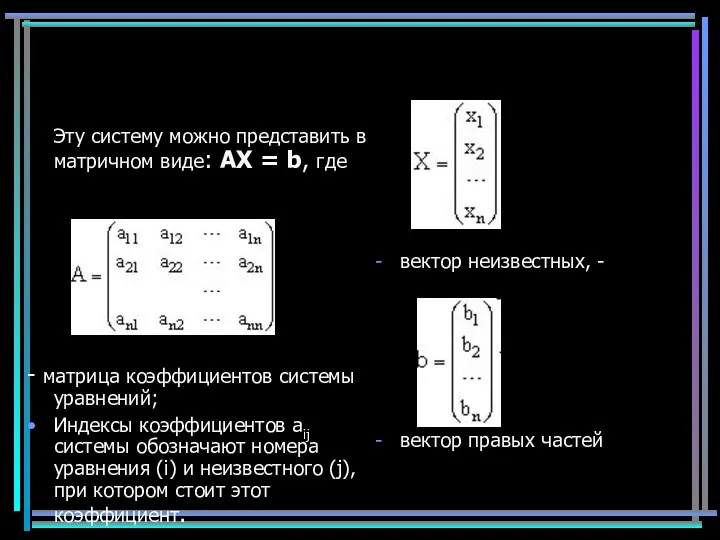
- 21. Эту систему можно представить в матричном виде: AX = b, где - матрица коэффициентов системы уравнений;
- 22. A·X = b А-1·A· X=А-1·b E · X=А-1·b X=А-1·b
- 23. Система уравнений называется совместной, если она имеет хотя бы одно решение, в противном случае система несовместна.
- 24. Порядок операций при вычислении обратной матрицы:
- 26. Матрица, обратная к диагональной матрице — диагональная матрица. Пример –доказать
- 27. Матрица, обратная к треугольной матрице — треугольная матрица
- 29. Найти решение системы уравнений: 4x1+2x2= 4 x1+x2= 2
- 30. Найти решение системы уравнений: 3x1-5x2= 22 x1+4x2= 5
- 32. Скачать презентацию
















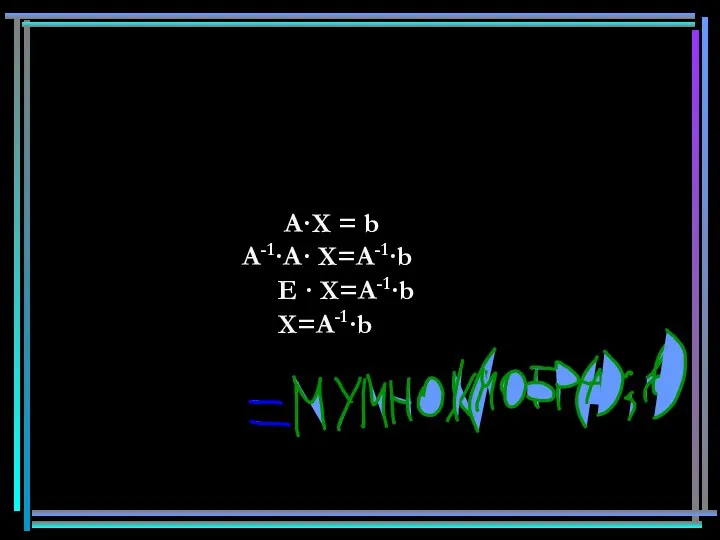








 Объем конуса
Объем конуса Геометрические тела и их проекции
Геометрические тела и их проекции Построение схемы по данному условию задачи
Построение схемы по данному условию задачи История чисел Работа ученицы 8 а класса МОУ СОШ №7 г. Соль – Илецка Оренбургской области Музапаровой Асемгуль
История чисел Работа ученицы 8 а класса МОУ СОШ №7 г. Соль – Илецка Оренбургской области Музапаровой Асемгуль Модель Гольдбетера циркадных ритмов нейроспоры
Модель Гольдбетера циркадных ритмов нейроспоры Логарифмические уравнения
Логарифмические уравнения Координатный луч
Координатный луч Засоби розв'язання задач оптимізації
Засоби розв'язання задач оптимізації Графоаналитические методы оценки параметров распределения (лекция 5)
Графоаналитические методы оценки параметров распределения (лекция 5) Методы исследования математических моделей
Методы исследования математических моделей Иррациональные уравнения
Иррациональные уравнения Нестандартные решения уравнений высших степеней
Нестандартные решения уравнений высших степеней Сумма углов треугольника
Сумма углов треугольника Решение квадратных уравнений
Решение квадратных уравнений Противоположные числа 6 класс. Презентация подготовлена учителем математики МОУ «СОШ №1 р.п. Новые Бурасы Саратовской обл
Противоположные числа 6 класс. Презентация подготовлена учителем математики МОУ «СОШ №1 р.п. Новые Бурасы Саратовской обл Интегрированный урок математики с Основами православной культуры 5 класс «Микрокалькулятор» «Икона» Учитель математики п.
Интегрированный урок математики с Основами православной культуры 5 класс «Микрокалькулятор» «Икона» Учитель математики п.  Basic transformations of graphs
Basic transformations of graphs Презентация по математике "Турнир математиков" - скачать
Презентация по математике "Турнир математиков" - скачать  Действия над рациональными числами
Действия над рациональными числами Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности Математика. Порядок действий
Математика. Порядок действий Занимательная математика Думай, считай, отгадывай!
Занимательная математика Думай, считай, отгадывай! Математическое моделирование: основные понятия и определения
Математическое моделирование: основные понятия и определения Сложение и вычитание векторов. Демонстрационный материал. 9 класс
Сложение и вычитание векторов. Демонстрационный материал. 9 класс Корреляционные зависимости
Корреляционные зависимости Динамическое программирование
Динамическое программирование Введение в теорию графов. Способы представления ориентированных и неориентированных графов
Введение в теорию графов. Способы представления ориентированных и неориентированных графов Формулы сокращённого умножения
Формулы сокращённого умножения