Содержание
- 2. Многочлен Лагранжа. Перейдем к случаю глобальной интерполяции. Будем искать интерполяционный многочлен в виде линейной комбинации многочленов
- 3. При этом потребуем, чтобы каждый многочлен li(x) обращался в нуль во всех узлах интерполяции, за исключением
- 4. этим условиям при i = 0 отвечает многочлен вида Действительно, l0(x0) = 1. При х =
- 5. Аналогично ………………………………………………………
- 6. Подставляя l0 , l1 ,…, ln в L(x) получим эта формула определяет интерполяционный многочлен Лагранжа.
- 7. Из формулы для L(x)можно получить выражения для линейной (n = 1) и квадратичной (n = 2)
- 8. Существует несколько обобщений интерполяционного многочлена Лагранжа. интерполяционные многочлены Эрмита. Здесь наряду со значениями функции yi в
- 9. Многочлен Ньютона. рассмотрим случай равноотстоящих значений аргумента, т. е. хi - хi-1 = h = const
- 10. Введем понятие конечных разностей. Пусть известны значения функции в узлах Составим разности значений функции: Эти значения
- 11. вторые разности функции: Аналогично составляются разности порядка k :
- 12. Конечные разности можно выразить непосредственно через значения функции. Например,
- 14. Аналогично для любого k можно написать Эту формулу можно записать и для значения разности в узле
- 15. Используя конечные разности, можно определить уk
- 16. Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем виде:
- 17. График многочлена должен проходить через заданные узлы, Эти условия используем для нахождения коэффициентов многочлена:
- 18. Найдем отсюда коэффициенты
- 19. Общая формула имеет вид
- 20. Подставляя эти выражения в формулу для N(x) получаем следующий вид интерполяционного многочлена Ньютона:
- 21. Данную формулу часто записывают в другом виде. Для этого вводится переменная тогда
- 22. тогда Полученное выражение называется первым интерполяционным многочленом Ньютона для интерполирования вперед.
- 23. Полученное выражение может аппроксимировать данную функцию на всем отрезке изменения аргумента [х0, хn]. Однако с точки
- 24. Для правой половины отрезка [х0, хn]. разности лучше вычислять справа налево. В этом случае
- 26. Скачать презентацию

















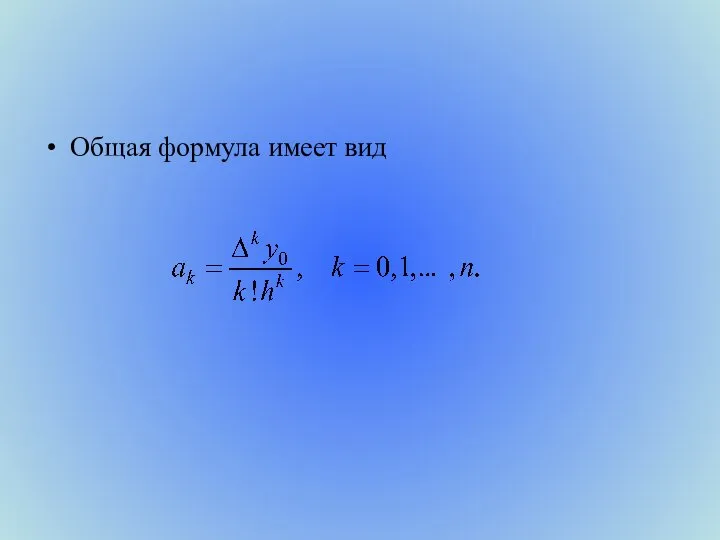




![Для правой половины отрезка [х0, хn]. разности лучше вычислять справа налево. В этом случае](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1147768/slide-23.jpg)
 Решение задач расчета надежности конструкций с многопараметрическим регулированием силовых факторов
Решение задач расчета надежности конструкций с многопараметрическим регулированием силовых факторов Квадратные уравнения
Квадратные уравнения Кубик Рубика. Наиболее простой вариант сборки кубика Рубика
Кубик Рубика. Наиболее простой вариант сборки кубика Рубика Взаимное расположение графиков линейной функции
Взаимное расположение графиков линейной функции Делимость чисел
Делимость чисел Линейная алгебра. Определители. (Лекция 2)
Линейная алгебра. Определители. (Лекция 2) Презентация на тему 2 класс Математический диктант №4
Презентация на тему 2 класс Математический диктант №4  Презентация по математике "Дифференцирование показательной и логарифмической функций." - скачать бесплатно
Презентация по математике "Дифференцирование показательной и логарифмической функций." - скачать бесплатно Тригонометрические функции углового аргумента
Тригонометрические функции углового аргумента Презентация по математике "Великие и знаменитые" - скачать
Презентация по математике "Великие и знаменитые" - скачать  Презентация на тему Умножение одночлена на многочлен
Презентация на тему Умножение одночлена на многочлен  Случайная величина (СВ) и закон ее распределения
Случайная величина (СВ) и закон ее распределения Иррациональные уравнения
Иррациональные уравнения Обработка многократно измеренных величин
Обработка многократно измеренных величин Презентация на тему Исследовательская работа на уроках математики
Презентация на тему Исследовательская работа на уроках математики  Координатный луч Урок математики в 5 классе Презентацию подготовил учитель математики МОУ»Шулкинская средняя школа» Романо
Координатный луч Урок математики в 5 классе Презентацию подготовил учитель математики МОУ»Шулкинская средняя школа» Романо Формализованное представление ЭА при автоматизированном проектировании
Формализованное представление ЭА при автоматизированном проектировании Разложение на простые множители
Разложение на простые множители Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Преобразование выражений, содержащих операцию извлечения квадратного корня
Преобразование выражений, содержащих операцию извлечения квадратного корня Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Аппроксимация закона распределения экспериментальных данных. Теоретические законы распределения случайных величин
Аппроксимация закона распределения экспериментальных данных. Теоретические законы распределения случайных величин Статистические характеристики: среднее арифметическое, мода, медиана
Статистические характеристики: среднее арифметическое, мода, медиана Иррациональные числа в древности и средние века. Действительные числа как бесконечные десятичные дроби в XVI – XVII вв
Иррациональные числа в древности и средние века. Действительные числа как бесконечные десятичные дроби в XVI – XVII вв Параллельные прямые
Параллельные прямые Презентация по математике "Типы систем счисления" - скачать бесплатно
Презентация по математике "Типы систем счисления" - скачать бесплатно Cан турында төшенчә. Сан һәм саналмыш
Cан турында төшенчә. Сан һәм саналмыш Десятичная запись дробных чисел. 5 класс, урок 99
Десятичная запись дробных чисел. 5 класс, урок 99