Содержание
- 2. Особенности средних величин: Они отражают то общее, что скрыто в каждой единице совокупности, они улавливают общие
- 3. Условия применения среднего: Средняя характеризует качественно однородную совокупность. Нельзя ограничиваться расчетом средней по всей совокупности, надо
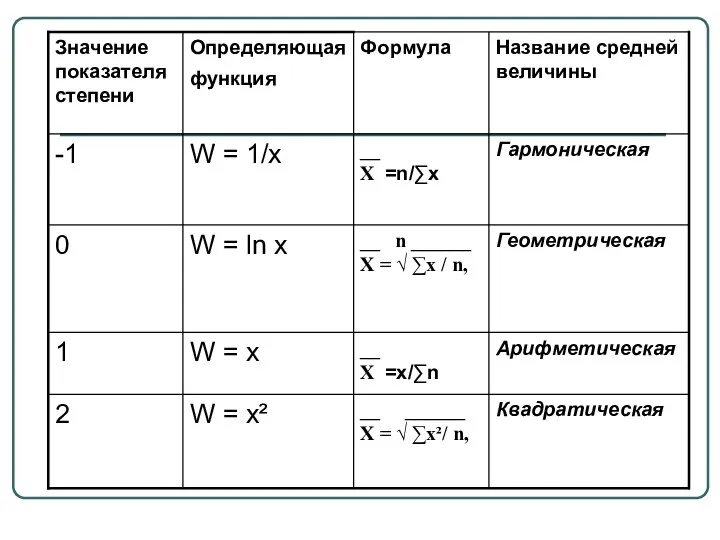
- 4. Вид степенной средней: __ k __________ Х = √ ∑хik / n, где Х – среднее
- 6. Хгар ≤ Хгеом ≤ Хар ≤ Хкв Это свойство степенных средних возрастать с повышением показателя степени
- 7. Средняя арифметическая Средняя арифметическая применяется тогда, когда объем варьирующего признака образуется как сумма значений признака у
- 8. Обозначим отдельные значения признака через х1, х2, х3, … хn, где n – объем совокупности. Тогда
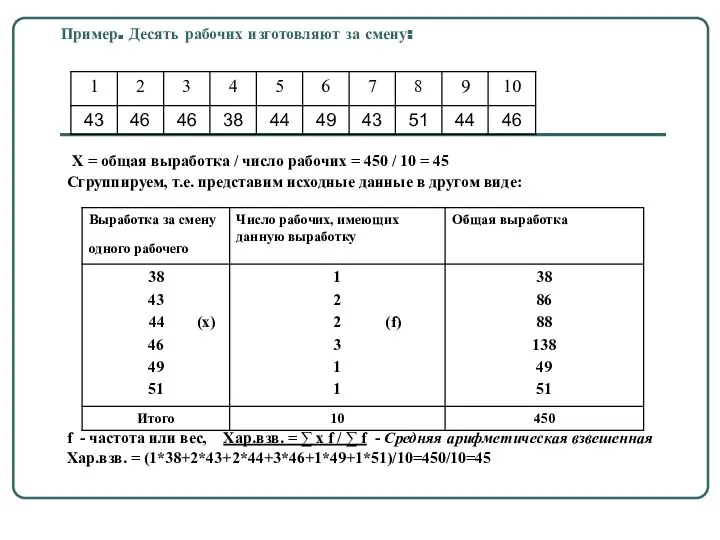
- 9. Пример. Десять рабочих изготовляют за смену: Х = общая выработка / число рабочих = 450 /
- 10. Статистическим весом (частотой) – называются числа, учитывающие значения величины признака (варианта) у единиц совокупности. Средняя арифметическая
- 11. d = f / ∑ f , где d – доля. Если доля выражается в процентах,
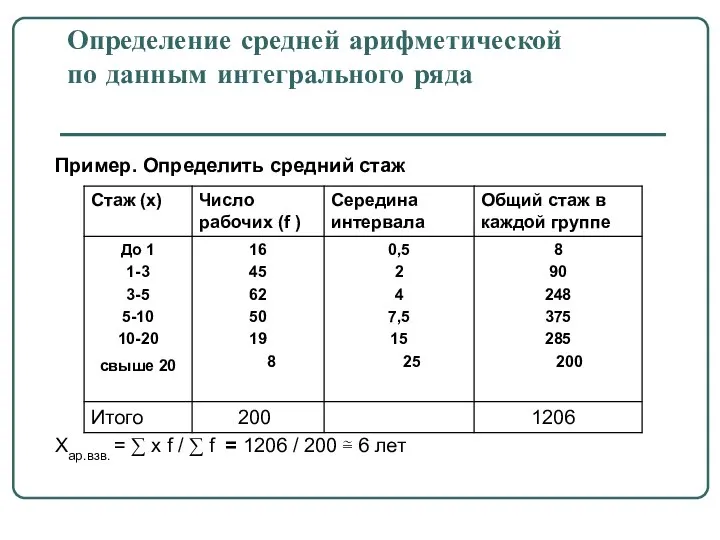
- 12. Определение средней арифметической по данным интегрального ряда Пример. Определить средний стаж Хар.взв. = ∑ x f
- 13. Свойства средней арифметической Алгебраическая сумма линейных отклонений индивидуальных значений признака от средней арифметической равна нулю. Если
- 14. Метод моментов или метод условного нуля Все варианты ряда уменьшают на одно и тоже число а:
- 16. Скачать презентацию










 Роль математики в изучении свойств атмосферы Земли Интегрированный урок (математика, география) 6 класс
Роль математики в изучении свойств атмосферы Земли Интегрированный урок (математика, география) 6 класс  Диаграммы. Таблицы
Диаграммы. Таблицы Объёмные тела и многогранники. Демонстрационный материал к уроку геометрии в 9 классе
Объёмные тела и многогранники. Демонстрационный материал к уроку геометрии в 9 классе Быстрый счет. Табличное сложение чисел от 11 до 20
Быстрый счет. Табличное сложение чисел от 11 до 20 Площадь круга
Площадь круга Регрессионный анализ
Регрессионный анализ Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Вероятность - классическое опеределение
Вероятность - классическое опеределение Тема : Измерение времени
Тема : Измерение времени  Квадрат
Квадрат Задачи на вклады и кредиты на ЕГЭ по математике
Задачи на вклады и кредиты на ЕГЭ по математике Вычисление производных. Формулы дифференцирования
Вычисление производных. Формулы дифференцирования Медиана треугольника
Медиана треугольника Расшифруйте название острова Диктант
Расшифруйте название острова Диктант  Решение уравнений
Решение уравнений Логическая задача со спичками
Логическая задача со спичками Операции с вероятностями по электроснабжению (задачи)
Операции с вероятностями по электроснабжению (задачи) 17.09.13 08.10.13 СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ Приведение дробей к общему знаменателю (п.10)
17.09.13 08.10.13 СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ Приведение дробей к общему знаменателю (п.10)  Первичная статистическая обработка результатов измерений случайной величины
Первичная статистическая обработка результатов измерений случайной величины Площадь и периметр прямоугольника
Площадь и периметр прямоугольника Презентация____
Презентация____ Цилиндр. Виды цилиндра
Цилиндр. Виды цилиндра Сложение натуральных чисел
Сложение натуральных чисел Математическая модель ведения боевых действий с учетом сил авиации и ПВО
Математическая модель ведения боевых действий с учетом сил авиации и ПВО Преобразования графиков функций
Преобразования графиков функций Формулы. Площадь прямоугольника
Формулы. Площадь прямоугольника Аттестационная работа. Организация исследовательской деятельности обучающихся на уроках математики и во внеурочное время
Аттестационная работа. Организация исследовательской деятельности обучающихся на уроках математики и во внеурочное время Призма. Выпуклые и невыпуклые призмы и антипризмы
Призма. Выпуклые и невыпуклые призмы и антипризмы