Содержание
- 2. 6.1. Основные понятия Математическая статистика занимается статистическим анализом результатов опытов или наблюдений, а также построением и
- 3. Статистический анализ и построение вероятностных моделей процессов и систем основаны на том, что измеряемые в процессе
- 4. Поэтому величина Х рассматривается как одномерная случайная величина, а результаты измерения х1, х2,…, хn этой величины,
- 5. Распределение признака Х в генеральной совокупности совпадает с теоретическим распределением вероятностной величины Х. Последнее называется распределением
- 6. Выборка из данной генеральной совокупности – это результаты ограниченного ряда наблюдений х1, х2,…, хn значений случайной
- 7. Число n наблюдений, образующих выборку, называют объемом выборки. Таким образом, вместо большой совокупности объектов изучается совокуп-
- 8. Это обеспечивается случайностью отбора. Виды отбора: 1) простой случайный: – повторный; – бесповторный; 2) сложный случайный:
- 9. Простой случайный отбор – производится без деления генеральной совокупности на части. Повторный отбор – отобранный объект
- 10. Типический отбор – генеральная совокупность делится на типы, из каждого типа случайно отбираются объекты пропорционально объёму
- 11. Разность между наибольшим и наименьшим значениями xi (i=1,…, n) из выборки называется размахом выборки. Взаимно независимые
- 12. Основные задачи математической статистики: 1. Определение закона распределения основного признака (наблюдаемой СВ); 2. Нахождение оценок неизвестных
- 13. 6.2.Статистическое распределение выборки Наблюдаемые значения xi (i=1,…,n) называют вариантами, а последовательность значений (вариант), записанных в возрастающем
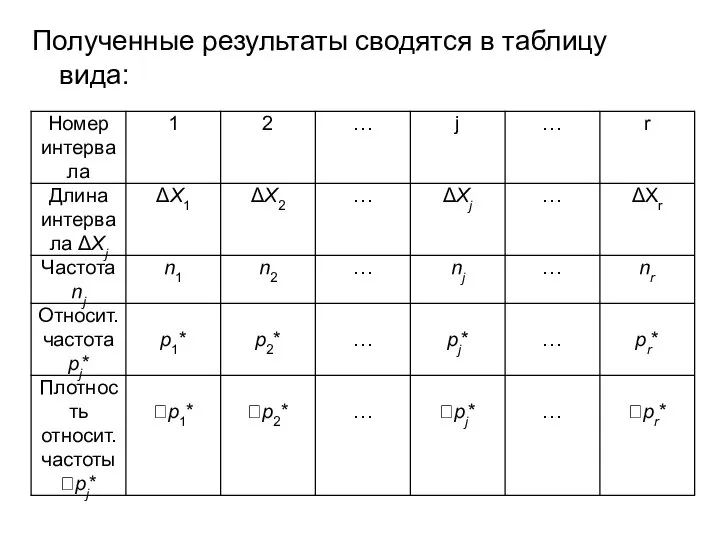
- 14. Статистическим распределением выборки называют перечень вариант xi и соответствующих им частот ni или относительных частот pi*.
- 15. Построение статистического ряда: размах выборки разбивается на q конечных (или бесконечных) интервалов Xj-0,5ΔXj 2. Количество интервалов
- 16. 3. В том случае, если полученные из опыта данные группируются вокруг некоторых значений, то желательно, чтобы
- 17. Выбор количества интервалов существенно зависит от объема выборки. Существуют такие рекомендации по использованию формулы Старджеса q=log2n+1≅3,32ln
- 18. Так как длина интервала hj может быть большой, а количество численных значений nj, попавших в него,
- 19. Полученные результаты сводятся в таблицу вида:
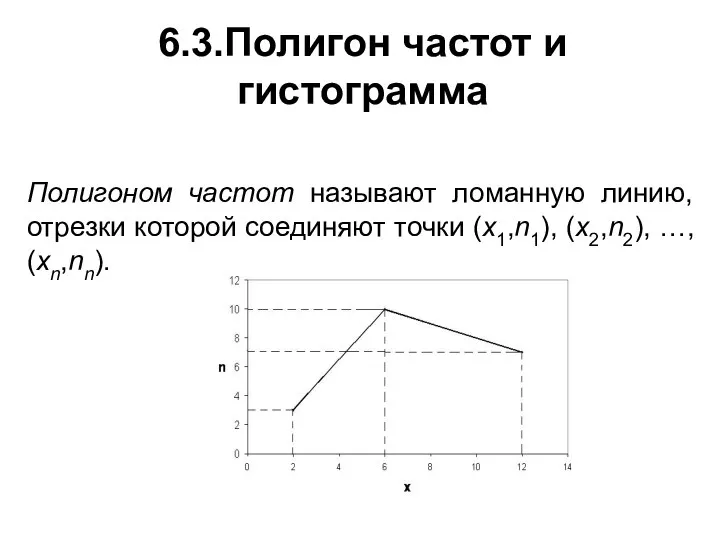
- 20. 6.3.Полигон частот и гистограмма Полигоном частот называют ломанную линию, отрезки которой соединяют точки (x1,n1), (x2,n2), …,
- 21. Для построения полигона частот на оси абсцисс откладывают варианты xi, а по оси ординат – соответствующие
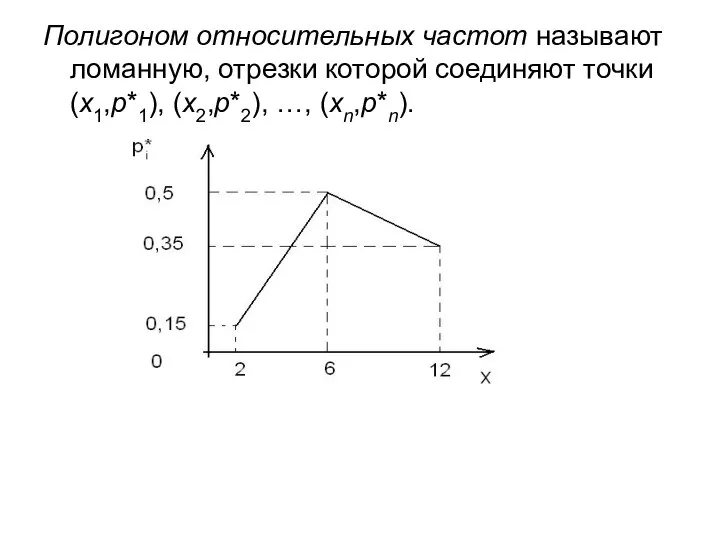
- 22. Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1,р*1), (x2,р*2), …, (xn,р*n).
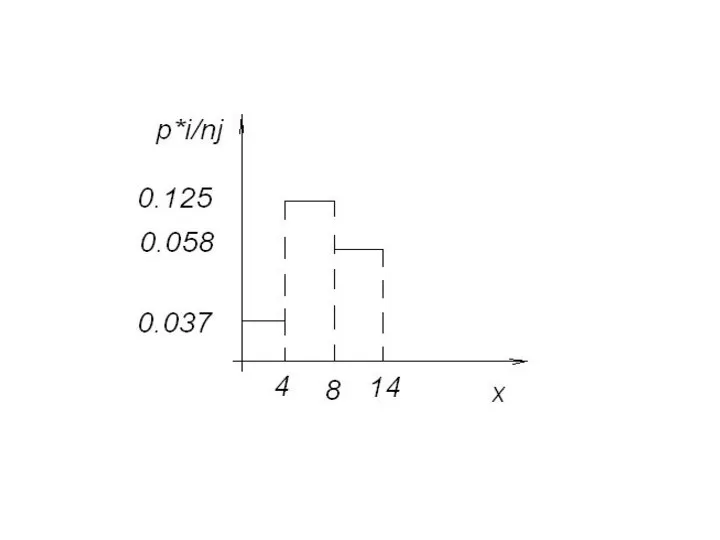
- 23. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиною hj=ΔXj, а высоты
- 24. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною hj
- 26. 6.4. Эмпирические функции распределения Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющей для каждого
- 27. Из т. Бернулли следует, что при неограниченном увеличении n относительная частота события X Эмпирическая (статистическая) функция
- 28. Это подтверждается тем, что F*(x) обладает всеми свойствами F(x): 1) значения эмпирической функции принадлежат отрезку [0;1];
- 30. Скачать презентацию























 Прогрессии вокруг нас
Прогрессии вокруг нас Параметрическая стандартизация. Ряды предпочтительных чисел
Параметрическая стандартизация. Ряды предпочтительных чисел Презентация по математике "Уравнение cos x=a" - скачать
Презентация по математике "Уравнение cos x=a" - скачать  Квадратный трехчлен
Квадратный трехчлен Математическая цепочка
Математическая цепочка Статистика. Статистические дисциплины
Статистика. Статистические дисциплины Понятие действительного числа
Понятие действительного числа Восхождение на Пик Победы
Восхождение на Пик Победы Углы, связанные с окружностью. Геометрия, 8 класс
Углы, связанные с окружностью. Геометрия, 8 класс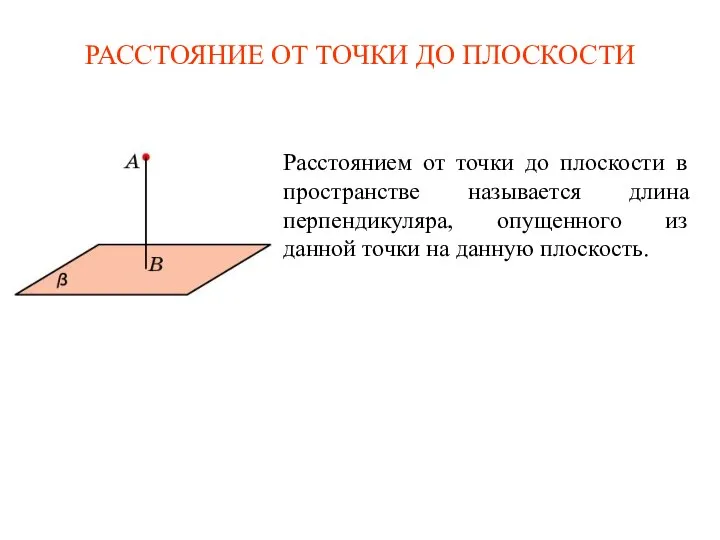 Расстояние от точки до плоскости в пространстве
Расстояние от точки до плоскости в пространстве Урок математики в 4 классе Учитель: Колупаев Д.В.
Урок математики в 4 классе Учитель: Колупаев Д.В.  Задачи по теме: Подобные треугольники
Задачи по теме: Подобные треугольники Смежные и вертикальные углы
Смежные и вертикальные углы Вероятность равновозможных событий
Вероятность равновозможных событий Сложение и вычитание десятичных дробей. Обобщающий урок
Сложение и вычитание десятичных дробей. Обобщающий урок Решение задач. Урок 22
Решение задач. Урок 22 Правильные многогранники
Правильные многогранники Основные понятия теории вероятности
Основные понятия теории вероятности Самостоятельная работа по геометрии. Тема: «Сумма углов треугольника.Неравенство треугольника.»
Самостоятельная работа по геометрии. Тема: «Сумма углов треугольника.Неравенство треугольника.» Тапкырлауның тарату үзлеген куллану. (6 класс)
Тапкырлауның тарату үзлеген куллану. (6 класс) Функция и её свойства
Функция и её свойства Геодезические сети. Лекция №4
Геодезические сети. Лекция №4 Daudzskaldņa šķēlums ar plakni. (11 klase)
Daudzskaldņa šķēlums ar plakni. (11 klase) Окремі випадки множення десяткових дробів
Окремі випадки множення десяткових дробів Секреты решения тестовых заданий по математике
Секреты решения тестовых заданий по математике Презентация по математике "Математический Турнир. Своя игра" - скачать
Презентация по математике "Математический Турнир. Своя игра" - скачать  Математические основы САПР. Mathcad. (Лекция 1)
Математические основы САПР. Mathcad. (Лекция 1) Обобщающий урок по теме «Делимость чисел. Простые и составные числа. Признаки делимости»
Обобщающий урок по теме «Делимость чисел. Простые и составные числа. Признаки делимости»