Статистические критерии в спортивной метрологии

1. Нормальное распределение и его свойства

Задачи оценки достоверности результатов и

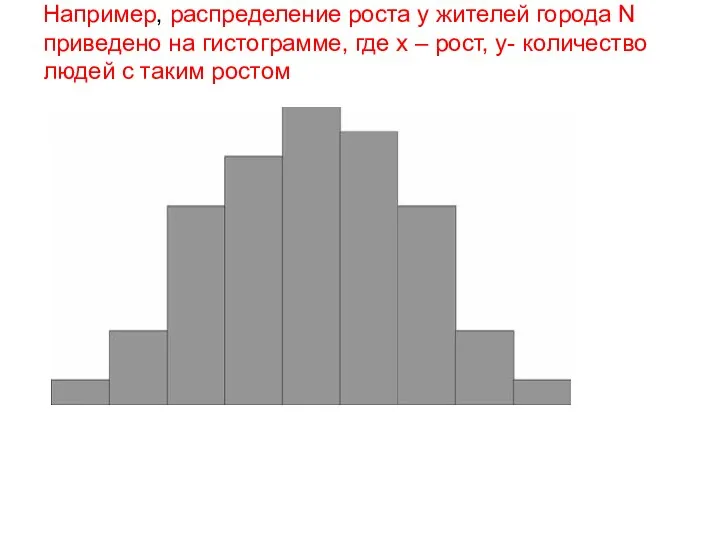
Например, распределение роста у жителей города N приведено на гистограмме, где

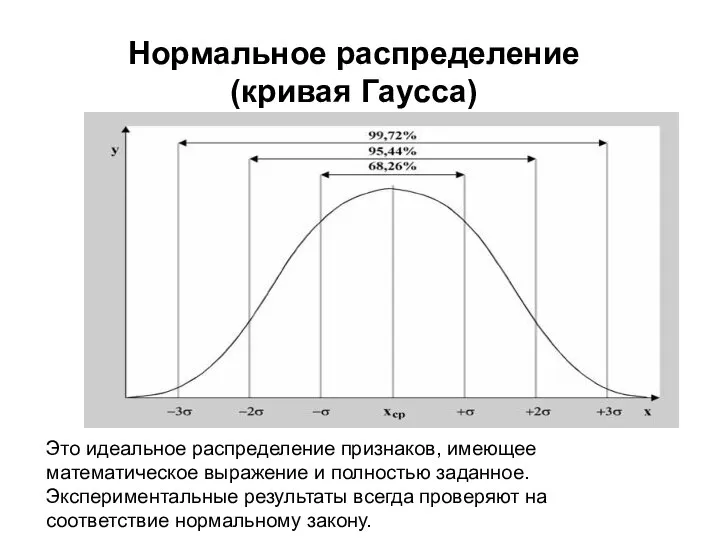
Нормальное распределение (кривая Гаусса)

Это идеальное распределение признаков, имеющее математическое выражение

Свойства нормального распределения

Относительная частота (вероятность) встречаемости конкретного диапазона может быть посчитана

Закон трех сигм (3 σ )

С вероятностью 99,7% все результаты попадают

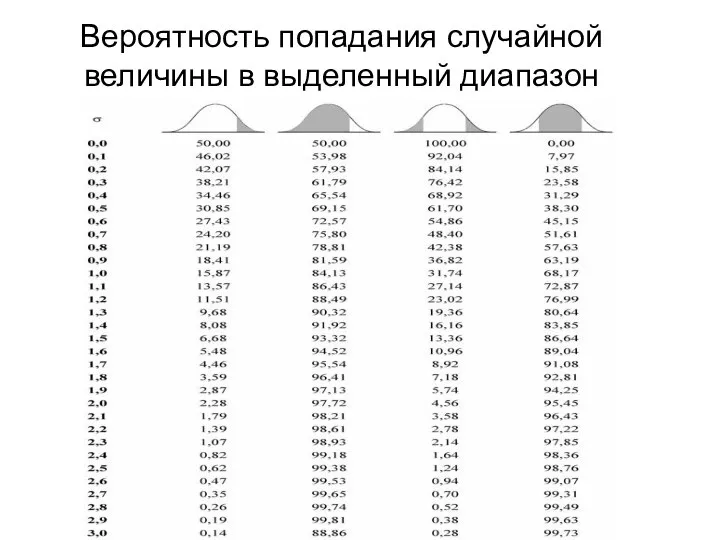
Вероятность попадания случайной величины в выделенный диапазон

2. Статистические критерии

Назначение: оценка достоверности различий средних величин

Виды критериев

Параметрические:
критерий Стьюдента, критерий Фишера
Условия применения: соответствие нормальному закону

3. Вычисление доверительного интервала

Доверительная вероятность – это вероятность с которой результаты

4. Алгоритм применения критериев для оценки достоверности
1. Задается доверительная вероятность (95%)

5. Критерий Стьюдента

Используется для сравнения средних выборочных значений двух различных по

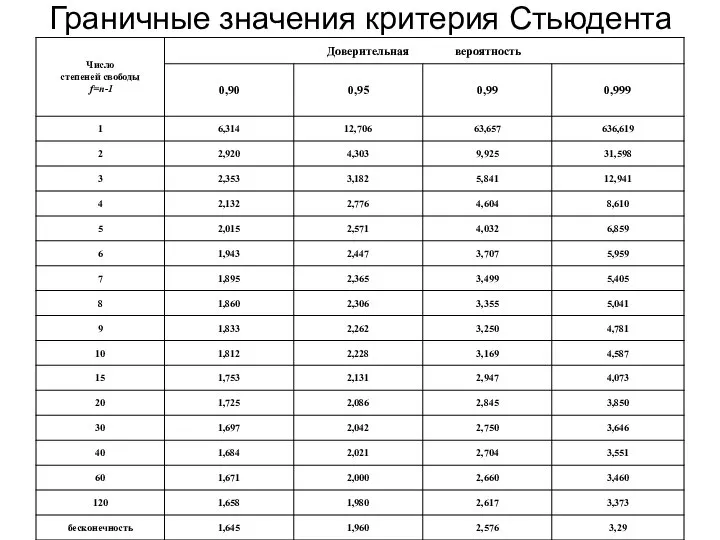
Граничные значения критерия Стьюдента

Пример 1

Достоверно ли различаются сила приводящих мышц рук у школьников

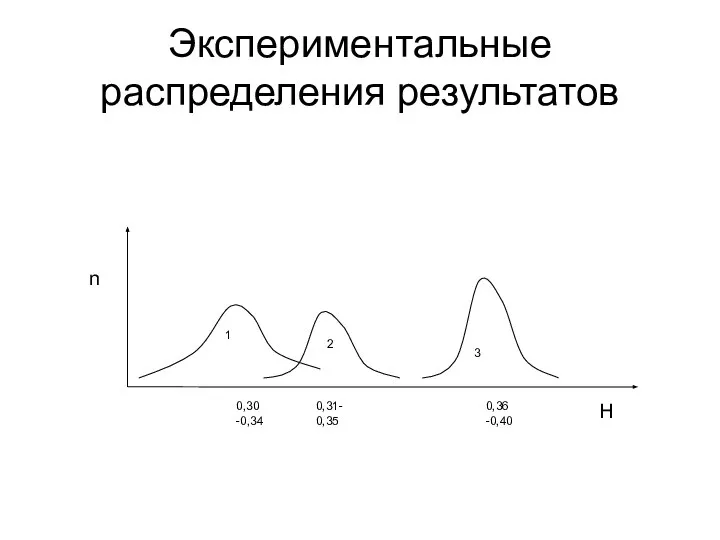
Экспериментальные распределения результатов

Р е ш е н и е

1. Х1-Х2 = 0,01 Х2-Х3

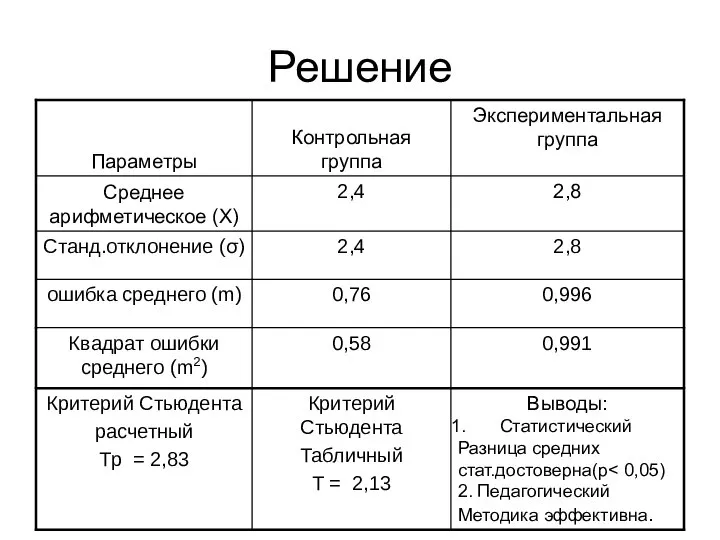
Пример 2

Сравните результаты экспериментальной (n=10) и контрольной группы (n=8) в

Решение

Алгоритм сравнения результатов по критерию Уайта

1. Результаты двух групп ранжируют вместе.
2.

Пример 3

Оценить эффективность «алгоритмической» методики обучения гимнастическим упражнениям. Оценки за выполнение

Решение

1. Проранжируем (упорядочим) результаты групп вместе и расставим ранги
Рез: 7,5 7,8