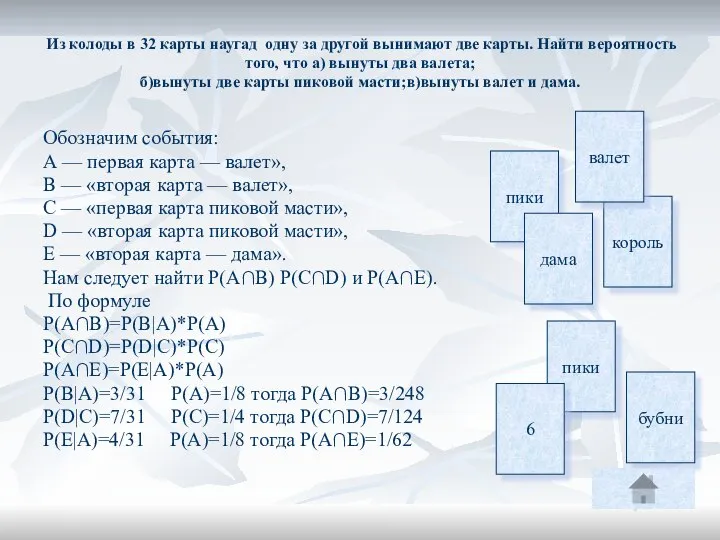
Брошены 2 игральные кости . Найти вероятность того, что на первой
кости выпало два очка при условии, что сумма очков, выпавших на двух костях, меньше 6
Пусть
А = {на первой кости выпало 2 очка},
В — {сумма очков, выпавших на двух костях, меньше 6}.
Событие В состоит из 10 элементарных cобытий:
В = {(1,1), (1,2), (2,1), (1,3), (3,1), (1,4), (4,1), (2,2), (2,3), (3,2)}.
Событие А, определяемое условием В (это значит, что исходы, благоприятствующие событию А, отбираются среди исходов, составляющих событие В), состоит из трех элементарных исходов опыта:
(2, 1), (2, 2), (2,3).
Поэтому искомая вероятность равна
Р(А|В) = 3/10









 Геометрический смысл двойного интеграла
Геометрический смысл двойного интеграла Длина окружности и площадь круга
Длина окружности и площадь круга Алгебра. Лекция 3. Простые и составные числа. Основная теорема арифметики
Алгебра. Лекция 3. Простые и составные числа. Основная теорема арифметики Обыкновенные дроби в стихах
Обыкновенные дроби в стихах Треугольники
Треугольники Сумма n-первых членов арифметической прогрессии
Сумма n-первых членов арифметической прогрессии Скалярное и векторное произведения векторов
Скалярное и векторное произведения векторов Первообразная и интеграл
Первообразная и интеграл Гетероскедастичность и ее последствия
Гетероскедастичность и ее последствия Задачи на движение
Задачи на движение Приращение функции
Приращение функции Игры с «природой». Метод платежной матрицы. Критерии Вальда, Сэвиджа, Лапласа, Гурвица
Игры с «природой». Метод платежной матрицы. Критерии Вальда, Сэвиджа, Лапласа, Гурвица Перпендикуляр и наклонная
Перпендикуляр и наклонная Интегрированный урок по физике и математике
Интегрированный урок по физике и математике Понятие цилиндра
Понятие цилиндра Общее повторение алгебры
Общее повторение алгебры Универсальная формула для решения текстовых задач на проценты
Универсальная формула для решения текстовых задач на проценты Задачи по геометрия на объем
Задачи по геометрия на объем Презентация на тему путешествие в прошлое города Воркута
Презентация на тему путешествие в прошлое города Воркута  Factorising Quadratics
Factorising Quadratics График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Непараметрические методы анализа
Непараметрические методы анализа Сложение, вычитание и умножение положительных и отрицательных чисел. Урок повторения и обобщения знаний
Сложение, вычитание и умножение положительных и отрицательных чисел. Урок повторения и обобщения знаний Равномерное движение по окружности. Решение задач
Равномерное движение по окружности. Решение задач Возведение степени в степень. Свойства действий со степенями
Возведение степени в степень. Свойства действий со степенями Основы программирования на языке Python. Логическая операция
Основы программирования на языке Python. Логическая операция Решение уравнений, содержащих знак абсолютной величины Автор: Хохлачева Мария Сергеевна, 8 «В» класс МОУ СОШ № 3 г.Волгограда
Решение уравнений, содержащих знак абсолютной величины Автор: Хохлачева Мария Сергеевна, 8 «В» класс МОУ СОШ № 3 г.Волгограда Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии