Содержание
- 2. Геометрия Планиметрия Стереометрия stereos телесный, твердый, объемный, пространственный
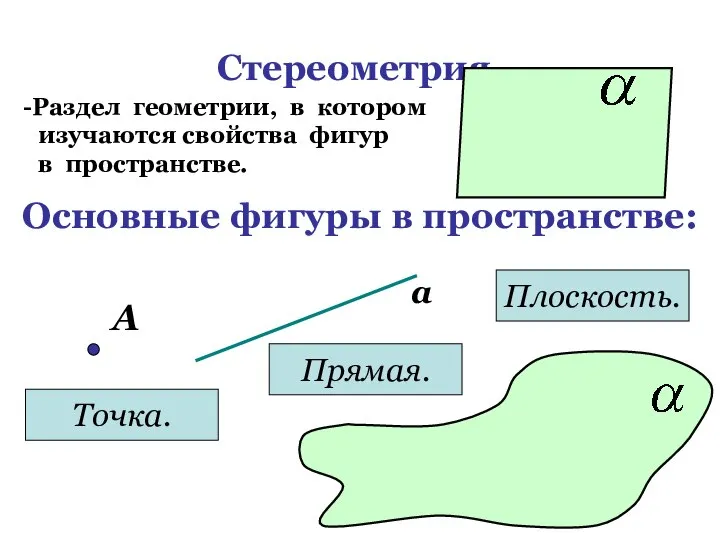
- 3. Стереометрия. Раздел геометрии, в котором изучаются свойства фигур в пространстве. Основные фигуры в пространстве: А Точка.
- 4. A, B, C, … a, b, c, … или AВ, BС, CD, …
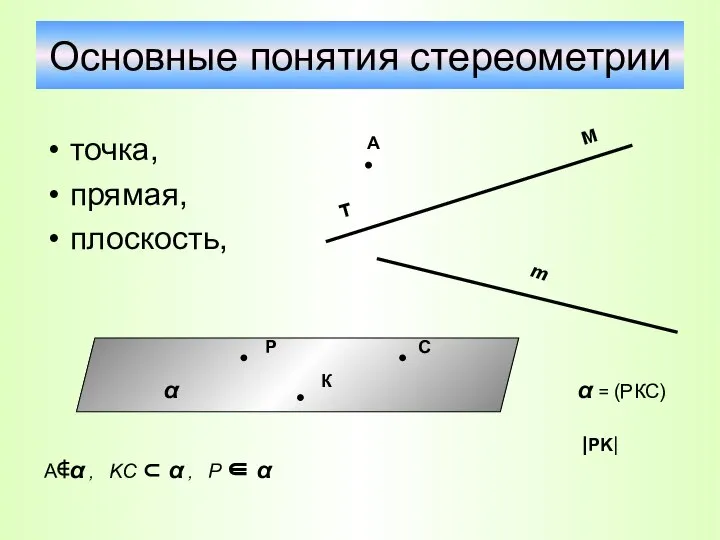
- 5. Основные понятия стереометрии точка, прямая, плоскость, α = (РКС) |PK| A∉α , KC ⊂ α ,
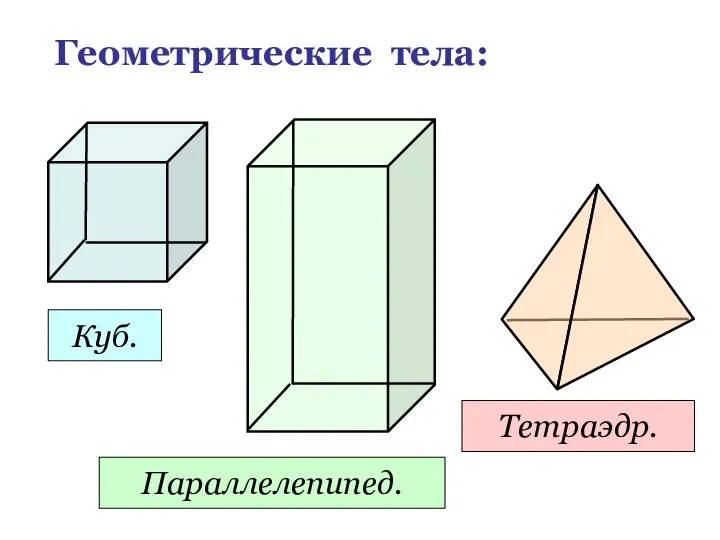
- 6. Геометрические тела: Куб. Параллелепипед. Тетраэдр.
- 7. Рассмотрим геометрические тела, поверхность которых составлена из многоугольников. Такие поверхности называются МНОГОГРАННИКАМИ Стороны и вершины этих
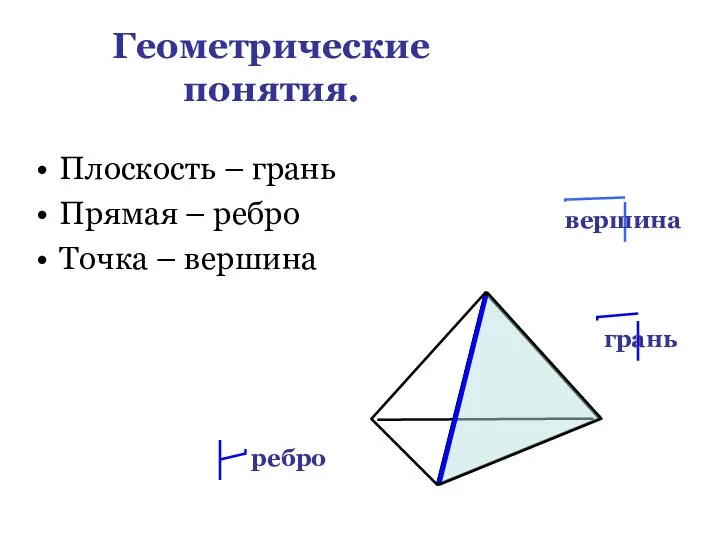
- 8. Геометрические понятия. Плоскость – грань Прямая – ребро Точка – вершина вершина грань ребро
- 9. Аксиома (от греч. axíõma – принятие положения) исходное положение научной теории, принимаемое без доказательства
- 10. Любые три точки лежат в одной плоскости. Любые четыре точки лежат в одной плоскости. Любые четыре
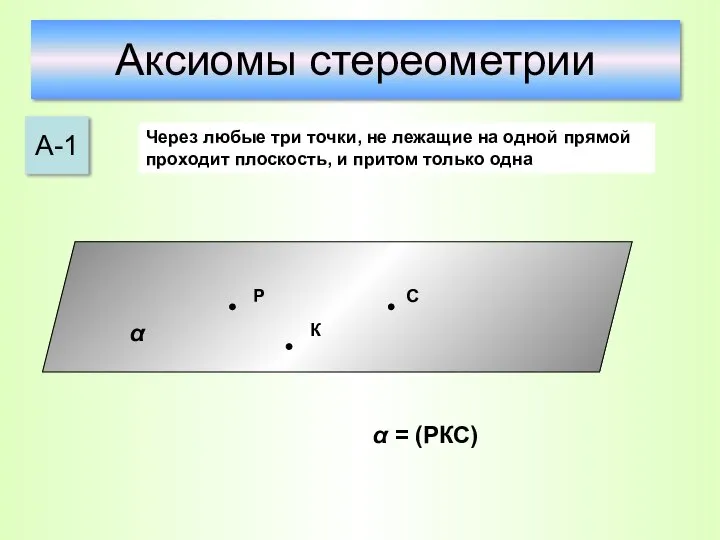
- 11. Аксиомы стереометрии А-1 Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом
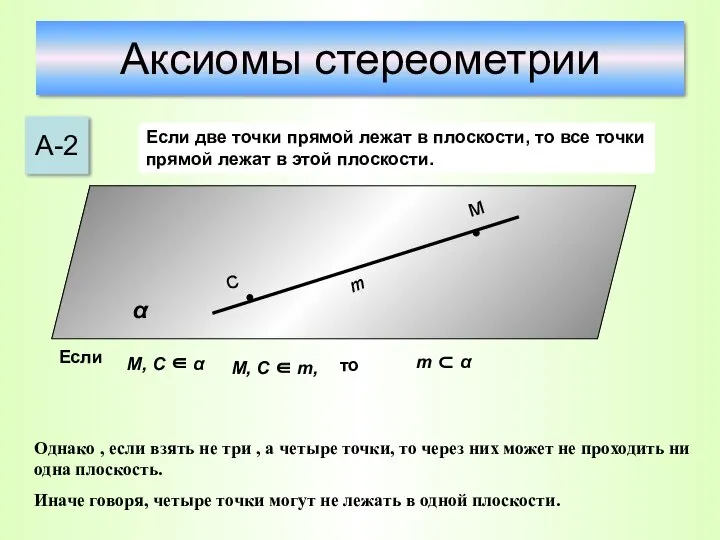
- 12. Аксиомы стереометрии А-2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в
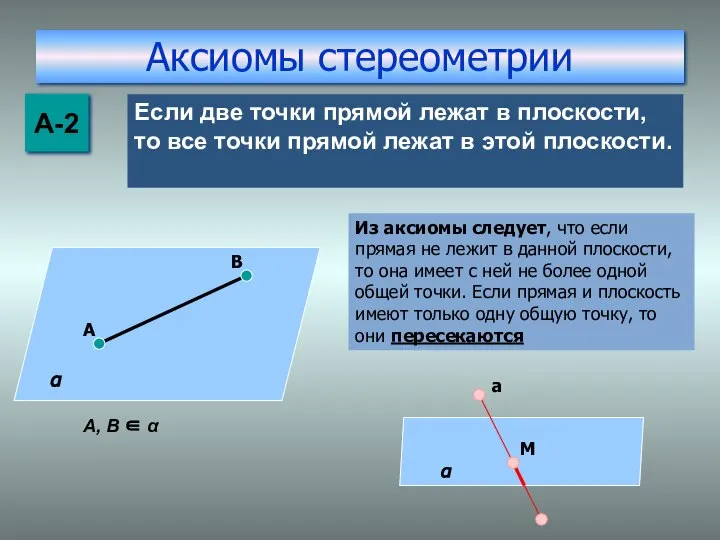
- 13. Аксиомы стереометрии А-2 Если две точки прямой лежат в плоскости, то все точки прямой лежат в
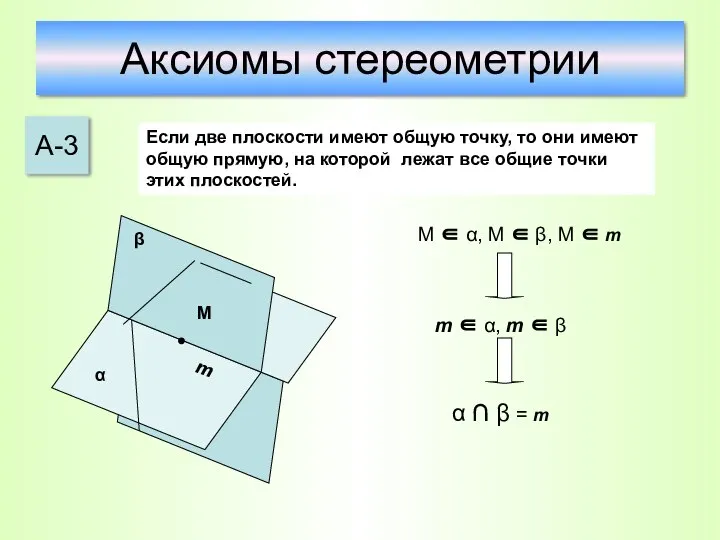
- 14. Аксиомы стереометрии А-3 Если две плоскости имеют общую точку, то они имеют общую прямую, на которой
- 15. АКСИОМЫ планиметрия стереометрия 1. Каждой прямой принадлежат по крайней мере две точки 2. Имеются по крайней
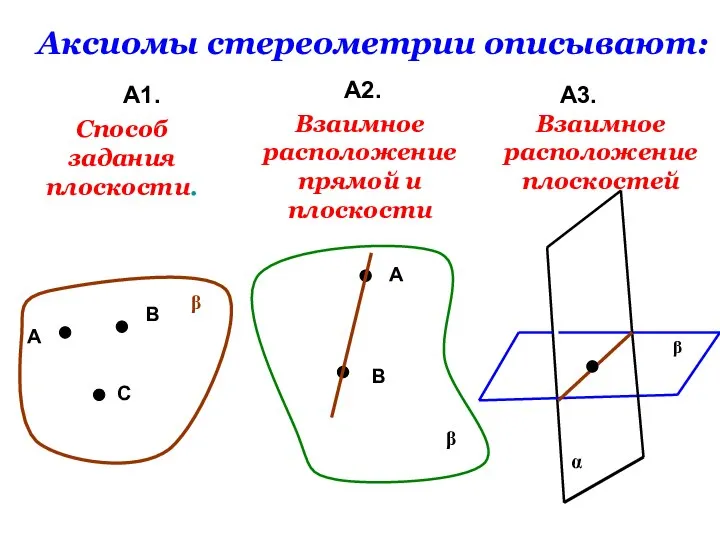
- 16. Аксиомы стереометрии описывают: А1. А2. А3. А В С β Способ задания плоскости. β А В
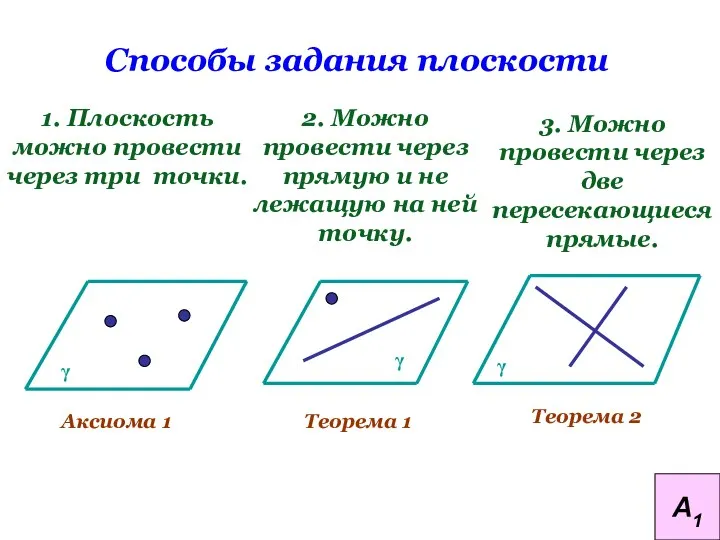
- 17. Способы задания плоскости 1. Плоскость можно провести через три точки. 2. Можно провести через прямую и
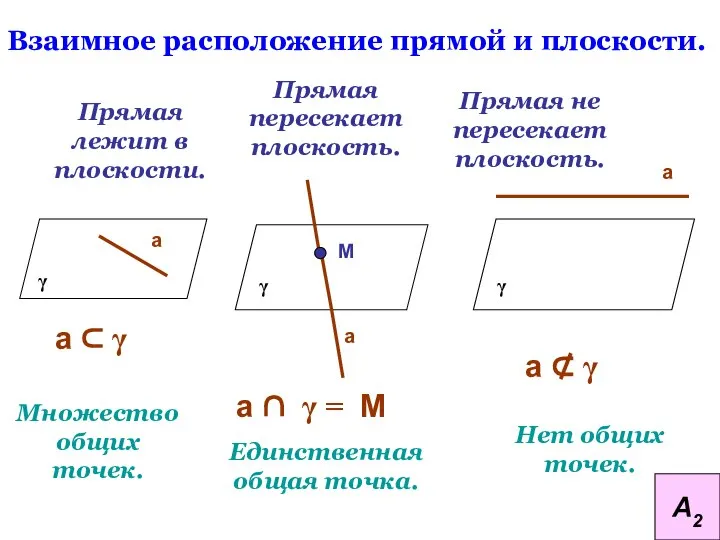
- 18. Взаимное расположение прямой и плоскости. Прямая лежит в плоскости. Прямая пересекает плоскость. Прямая не пересекает плоскость.
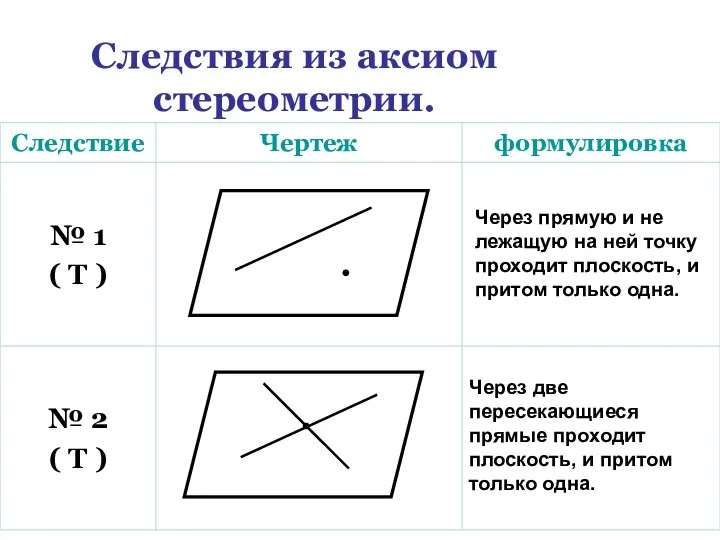
- 19. Следствия из аксиом стереометрии. Через прямую и не лежащую на ней точку проходит плоскость, и притом
- 20. СЛЕДСТВИЯ ИЗ АКСИОМ Т-1 Через любую прямую и не принадлежащую ей точку можно провести плоскость, и
- 21. СЛЕДСТВИЯ ИЗ АКСИОМ Т-2 Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.
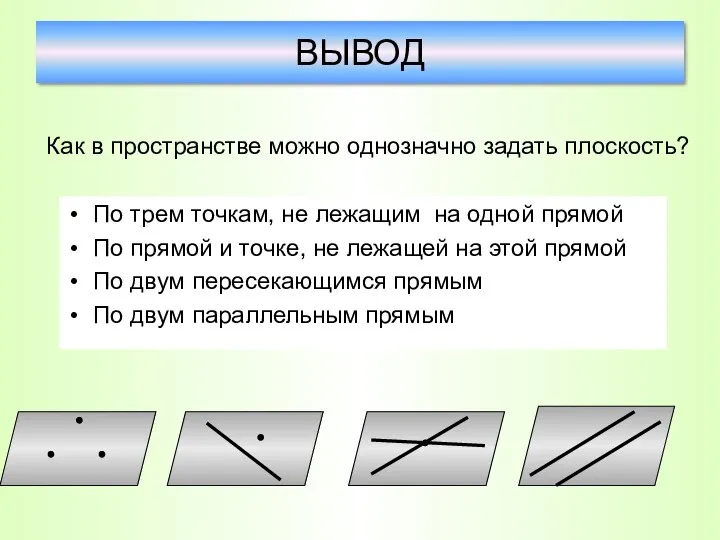
- 22. По трем точкам, не лежащим на одной прямой По прямой и точке, не лежащей на этой
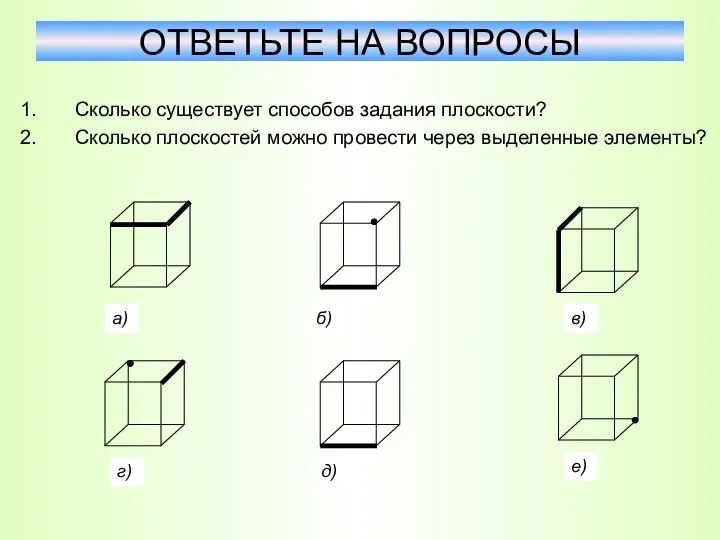
- 23. Сколько существует способов задания плоскости? Сколько плоскостей можно провести через выделенные элементы? ОТВЕТЬТЕ НА ВОПРОСЫ а)
- 24. Дз Выучи наизусть формулировки аксиом и следствий Ответь на вопросы№3,4,5,6,8,10,13 Подготовь конспект параграфа (формулировки и определения)
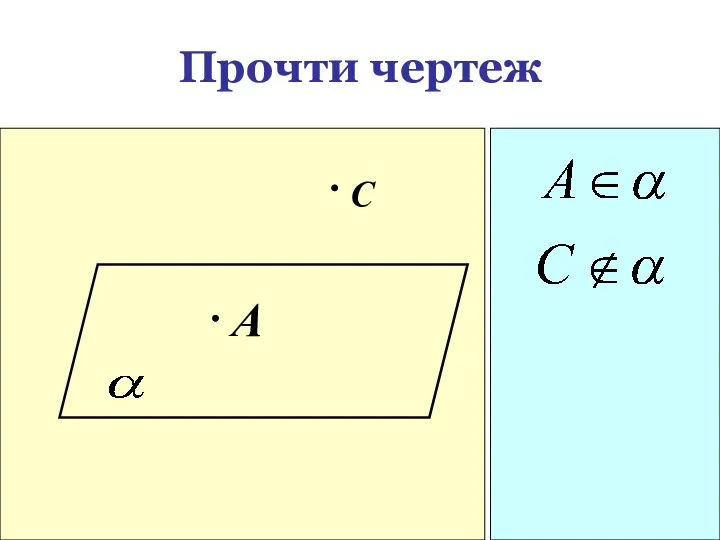
- 25. Прочти чертеж A С
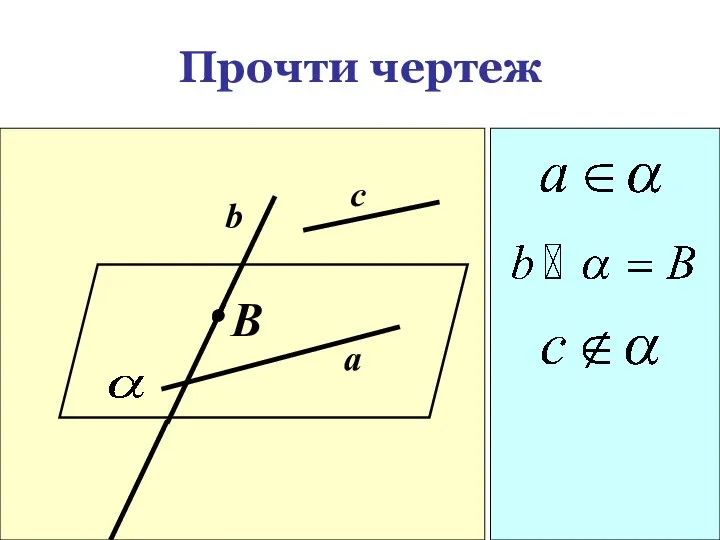
- 26. Прочти чертеж B c b a
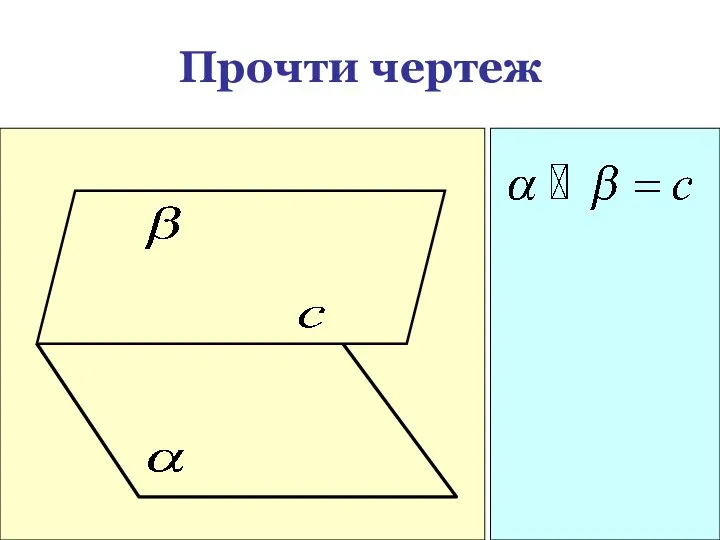
- 27. Прочти чертеж
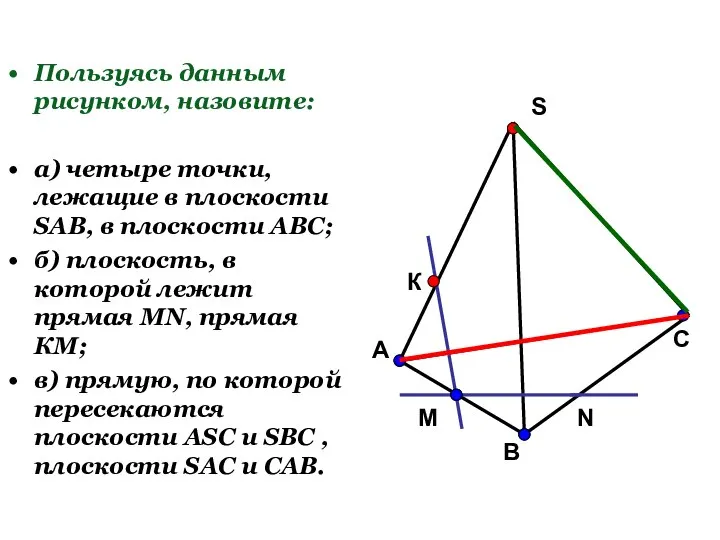
- 28. Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; б) плоскость,
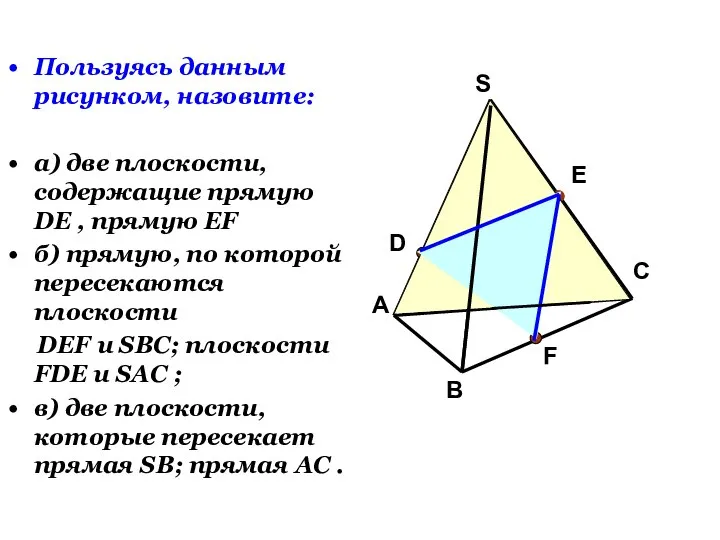
- 29. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE , прямую EF б) прямую, по
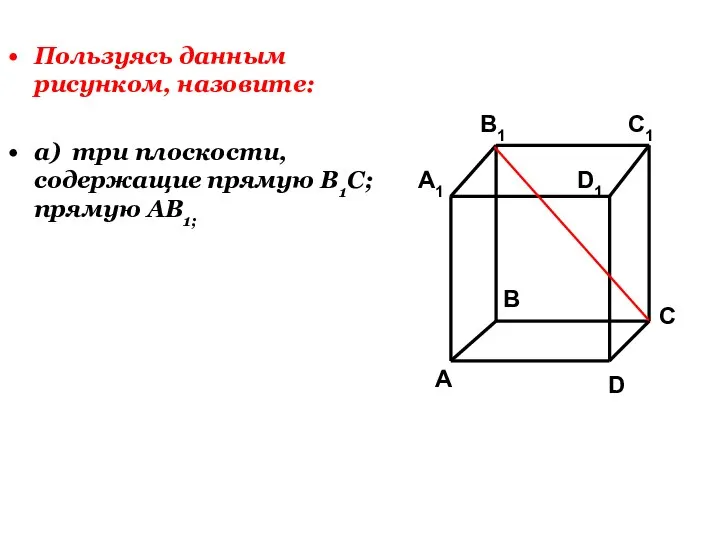
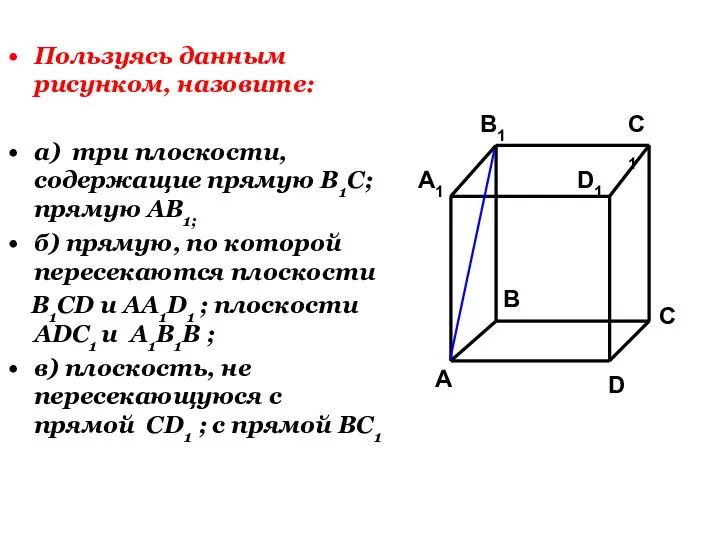
- 30. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1;
- 31. А А1 В В1 С D1 D C1 а) В1С ?
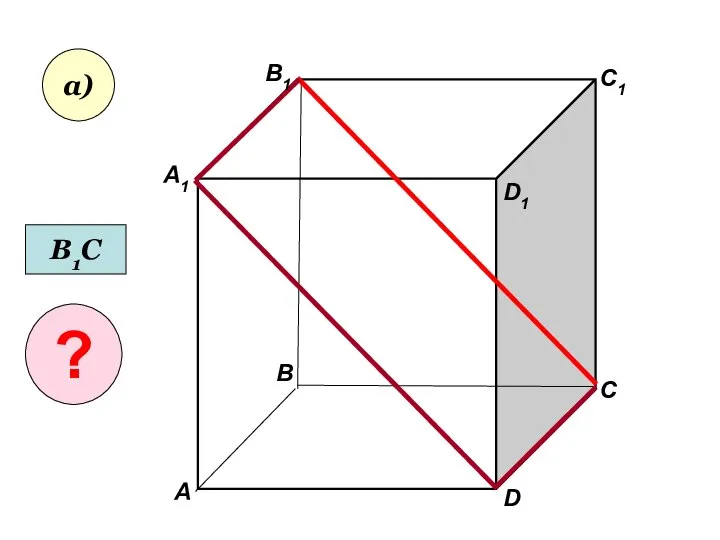
- 32. А А1 В В1 С D1 D C1 а) В1С ?
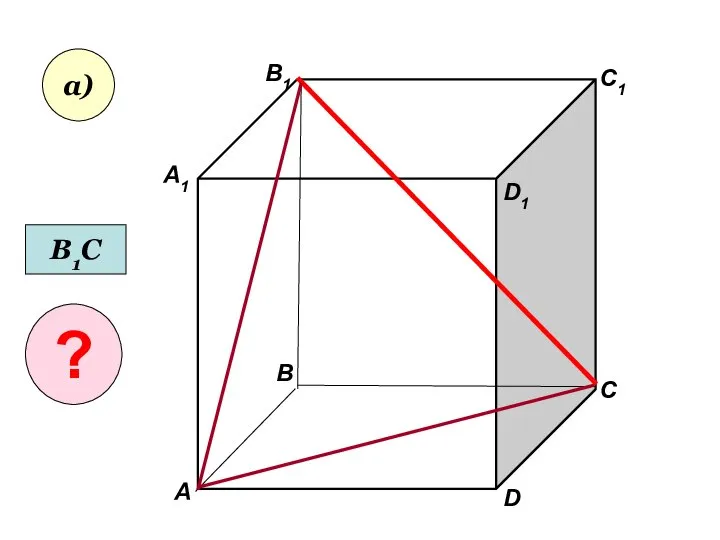
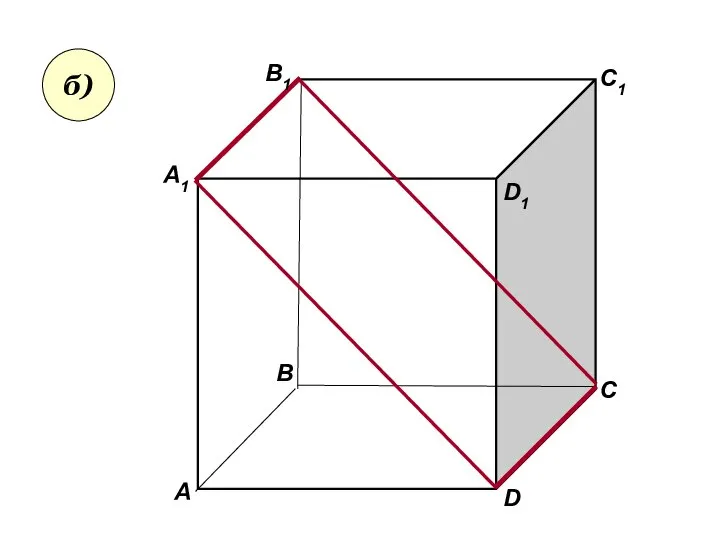
- 33. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 34. А А1 В В1 С D1 D C1 б)
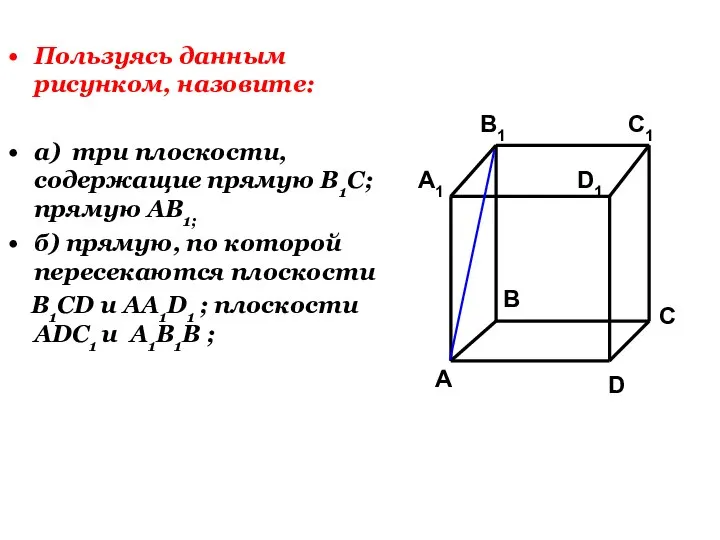
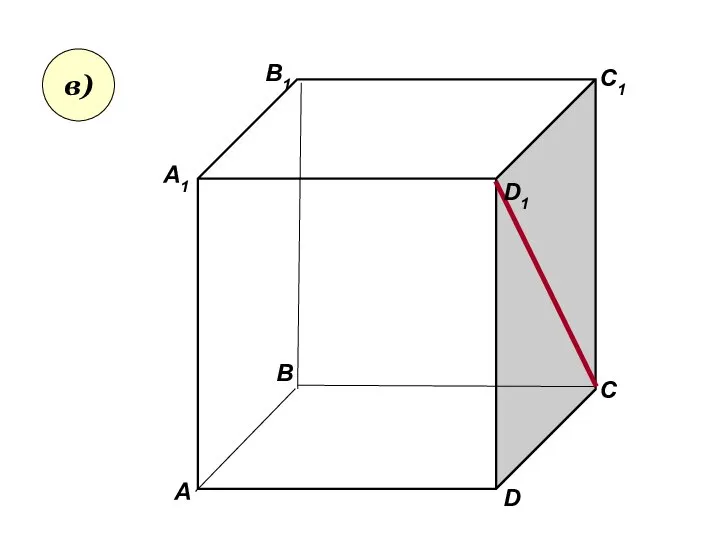
- 35. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой
- 36. А А1 В В1 С D1 D C1 в)
- 38. Скачать презентацию








 Системы счисления с древних времён до современного мира
Системы счисления с древних времён до современного мира Презентация по математике "Параллельность прямых" - скачать
Презентация по математике "Параллельность прямых" - скачать  Ямало-Ненецкий автономный округ Изучение сечений в стереометрии с помощью компьютера
Ямало-Ненецкий автономный округ Изучение сечений в стереометрии с помощью компьютера Деление десятичных дробей на натуральные числа
Деление десятичных дробей на натуральные числа Задачи на построение. Геометрия в 7-м классе
Задачи на построение. Геометрия в 7-м классе Перпендикулярность прямых, перпендикулярность прямой и плоскости
Перпендикулярность прямых, перпендикулярность прямой и плоскости Интегралы, зависящие от параметра
Интегралы, зависящие от параметра Числовые промежутки
Числовые промежутки Презентация на тему Приложения производной Алгебра 10
Презентация на тему Приложения производной Алгебра 10 Булеві функції
Булеві функції Решение задач с использованием признаков равенства треугольников
Решение задач с использованием признаков равенства треугольников Особливості пошуку екстремуму функції відгуку другого порядку
Особливості пошуку екстремуму функції відгуку другого порядку Усечённая пирамида
Усечённая пирамида Исторические задачи
Исторические задачи Планарные графы
Планарные графы Понятие логарифма
Понятие логарифма Теорема Шеннона
Теорема Шеннона Правила приближенных вычислений. Выполнение практической работы. Расчет погрешности результата измерения
Правила приближенных вычислений. Выполнение практической работы. Расчет погрешности результата измерения Одночлен и его стандартный вид_
Одночлен и его стандартный вид_ Презентация на тему Прямоугольный параллелепипед. Куб.
Презентация на тему Прямоугольный параллелепипед. Куб.  ДПА 11 класс Первообразная и интеграл
ДПА 11 класс Первообразная и интеграл Математика. Задания на лето. Часть 5
Математика. Задания на лето. Часть 5 Задания из открытого банка ЕГЭ
Задания из открытого банка ЕГЭ Определение степени. Основное свойство степени
Определение степени. Основное свойство степени Особенности выполнения заданий ВПР по математике
Особенности выполнения заданий ВПР по математике Презентация на тему Сложение десятичных дробей
Презентация на тему Сложение десятичных дробей Вычитание из 15
Вычитание из 15 Морской бой. Правила игры. Тема: Математика
Морской бой. Правила игры. Тема: Математика