Содержание
- 2. Основні поняття теорії ймовірностей Експеримент (випробування) – може повторюватися багаторазово при незмінних умовах, при цьому результат
- 3. ПРИКЛАД ВИКОРИСТАННЯ ОСНОВНИХ ПОНЯТЬ Кубик кладеться в стаканчик, струшується, з стаканчика викочується на стіл і котиться
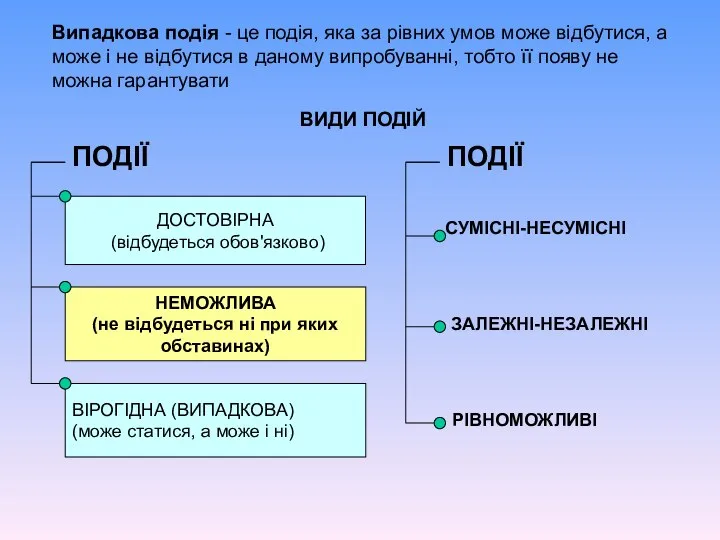
- 4. ВИДИ ПОДІЙ ПОДІЇ ДОСТОВІРНА (відбудеться обов'язково) НЕМОЖЛИВА (не відбудеться ні при яких обставинах) ВІРОГІДНА (ВИПАДКОВА) (може
- 5. ОПЕРАЦІЇ НАД ПОДІЯМИ. ДІАГРАМИ ЕЙЛЕРА Сума подій добуток протилежна подія або … або і … і
- 7. ФОРМУЛЫ КОМБИНАТОРИКИ И ПРИМЕРЫ ИХ ПРИМЕНЕНИЯ Перестановки n місць n об’єктів Сполучення Вибір m об’єктів з
- 8. Теорема додавання ймовірностей несумісних подій Імовірність появи однієї з двох несумісних подій дорівнює сумі ймовірностей цих
- 9. Теорема додавання ймовірностей сумісних подій Ймовірність реалізації однієї із двох сумісних випадкових подій, дорівнює сумі ймовірностей
- 10. Теорема множення ймовірностей Імовірність події , обчислена за умови, що відбулася інша подія , називається умовною
- 11. Імовірність появи хоча б однієї події Імовірність настання події , що полягає в появі хоч би
- 12. Формула повної ймовірності Ймовірність події , що може настати лише за умови появи однієї з несумісних
- 13. Повторні незалежні випробування Формула Бернуллі. Імовірність того, що в n незалежних випробуваннях, в кожному з яких
- 14. Формула Пуассона: Використовують для рішення задач за схемою Бернулі, коли і
- 15. Формула Муавра-Лапласа Використовують для рішення задач за схемою Бернулі, коли і Для інтервала значень:
- 17. Скачать презентацию













 Теория вероятностей. Способность предвидеть возможные варианты будущего
Теория вероятностей. Способность предвидеть возможные варианты будущего Необычные геометрические фигуры. 7 класс
Необычные геометрические фигуры. 7 класс Додавання і віднімання в межех 20. Веселий потяг
Додавання і віднімання в межех 20. Веселий потяг Задачи оптимизации производства товаров и услуг
Задачи оптимизации производства товаров и услуг Тест по теме функция
Тест по теме функция Анализ геометрической формы
Анализ геометрической формы Проценты. Нахождение процентов от числа. Нахождение числа по его процентам
Проценты. Нахождение процентов от числа. Нахождение числа по его процентам Контрольно-измерительные инструменты для контроля плоскости
Контрольно-измерительные инструменты для контроля плоскости Определение вектора
Определение вектора Урок 105. Признаки делимости на 2, 5, 10, 4 и 25. Урок 105
Урок 105. Признаки делимости на 2, 5, 10, 4 и 25. Урок 105 Аксиомы стереометрии
Аксиомы стереометрии Грегор Мендель Закон единообразия гибридов Закон расщепления признаков
Грегор Мендель Закон единообразия гибридов Закон расщепления признаков Таблица умножения и деления на 7. Тренажёр
Таблица умножения и деления на 7. Тренажёр Игра «Кто хочет стать отличником?»
Игра «Кто хочет стать отличником?» Подготовка к контрольной работе
Подготовка к контрольной работе Математическая викторина
Математическая викторина Сценарий медиаурока с компьютером. 7 класс
Сценарий медиаурока с компьютером. 7 класс Түзу мен жазықтықтың параллельдігі және перпендикулярлығы
Түзу мен жазықтықтың параллельдігі және перпендикулярлығы Симметрия в мире и мир симметрии
Симметрия в мире и мир симметрии Занимательная математика Своя игра. 12 вопросов. 5 класс
Занимательная математика Своя игра. 12 вопросов. 5 класс Элементы корреляционного и регрессионного анализа
Элементы корреляционного и регрессионного анализа Использование графика производной для определения свойств функции
Использование графика производной для определения свойств функции Модели эксплуатации на основе метода динамики средних
Модели эксплуатации на основе метода динамики средних Vienkāršās formas
Vienkāršās formas Тест по теме: "Окружность"
Тест по теме: "Окружность" Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Презентация на тему Меры времени 3 класс
Презентация на тему Меры времени 3 класс  Смежные и вертикальные углы
Смежные и вертикальные углы