Содержание
- 2. Теория вероятностей УГТУ-УПИ 2008г. М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко, Н.М.Рыбалко, А.Б.Соболев Лекция 8 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- 3. Цель лекции: 1. Овладеть соответствующим математическим аппаратом для дальнейшего изучения курса математики, демонстрировать и использовать математические
- 4. Формируемые компетенции по ФГОС:
- 5. Лекция 8 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- 6. Математическая статистика – раздел математики, изучающий методы сбора и анализа результатов наблюдений массовых случайных явлений с
- 8. результаты наблюдений (экспериментов) процесс наблюдений может корректироваться на основании предварительных результатов (последовательный анализ) Источники информации априорная
- 9. Следует заметить, что степень обоснованности применения априорной информации зависит от компетентности и добросовестности конкретного исследователя и
- 10. . Частые задачи математической статистики Предварительная обработка данных упорядочение результатов наблюдения или эксперимента, представление их в
- 11. Современная математическая статистика может быть определена как теория принятия решений в условиях неопределенности. Она включает в
- 12. Генеральная и выборочная совокупности. Способы отбора Если нужно изучить, как в совокупности однородных объектов распределен некоторый
- 13. Основные определения Выборкой или выборочной совокупностью называют совокупность случайно отобранных объектов. Генеральной совокупностью называют исходное множество
- 14. Для упрощения вычислений при очень большом объеме генеральной совокупности часто принимают, что ее объем бесконечен. Подобное
- 15. Выборка называется повторной, если случайно отобранный для обследования объект возвращается в генеральную совокупность перед отбором следующего
- 16. Чтобы по данным выборки можно было судить о всей совокупности, необходимо, чтобы члены выборки представляли ее
- 17. 1) случайный отбор элементов совокупности, 2) равновероятность попадания в выборку любого элемента генеральной совокупности, 3) достаточно
- 18. Если элементы извлекаются по одному из генеральной совокупности, говорят о простом случайном отборе (может быть повторным
- 19. Типический отбор осуществляется следующим образом: генеральная совокупность делится на “типические” части, из каждой части производится случайный
- 20. Статистическое распределение выборки
- 21. статистическим распределением выборки или статистическим рядом Называется перечень вариант и соответствующих им частот (или относительных частот)
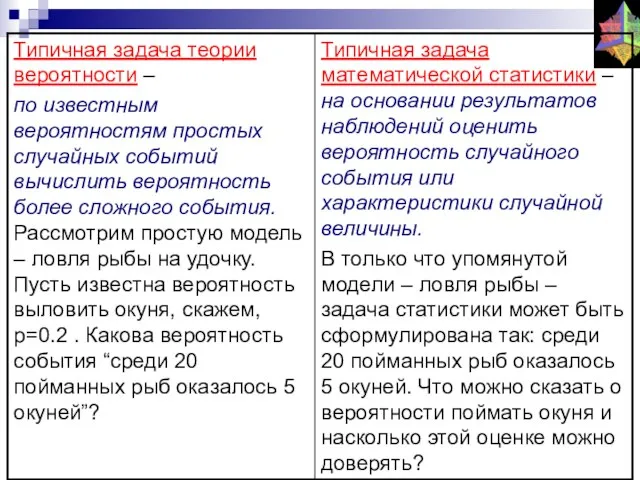
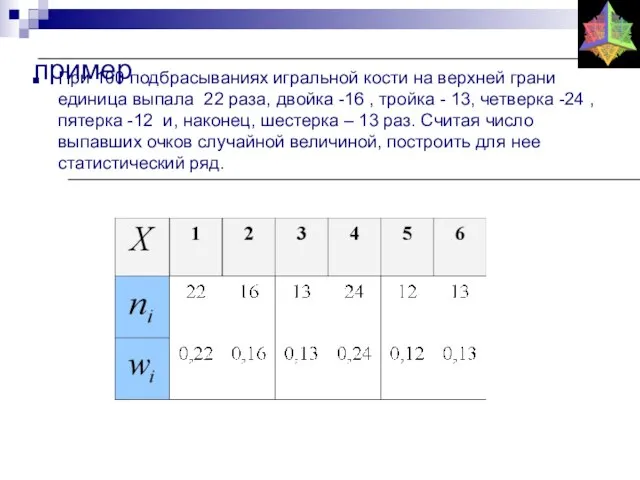
- 22. пример При 100 подбрасываниях игральной кости на верхней грани единица выпала 22 раза, двойка -16 ,
- 23. В том случае, если число значений случайной величины X велико, или есть основания полагать, что случайная
- 24. Значения вариант группируют по промежуткам (обычно одинаковой длины), в первой строке указывается промежуток, во второй –
- 25. интервальный статистический ряд Значения вариант группируют по промежуткам (обычно одинаковой длины), в первой строке указывается промежуток,
- 26. пример Пусть измерен рост 50 случайно выбранных человек с точностью до 1 см (результаты приведены ниже).
- 27. Упорядочим данные выборки по возрастанию (ранжируем выборку): 152, 153, 156, 158, 159, 160, 160, 160, 163,
- 28. Построим интервальный статистический ряд.
- 29. Полигон и гистограмма Для наглядности часто используют графические изображения статистических рядов: для дискретного ряда - полигон,
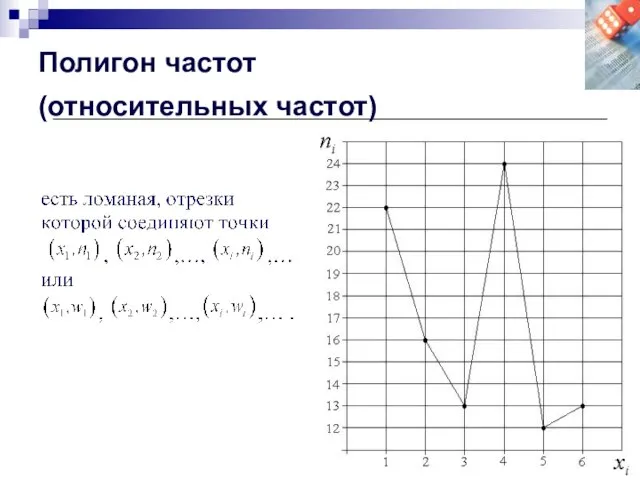
- 30. Полигон частот (относительных частот)
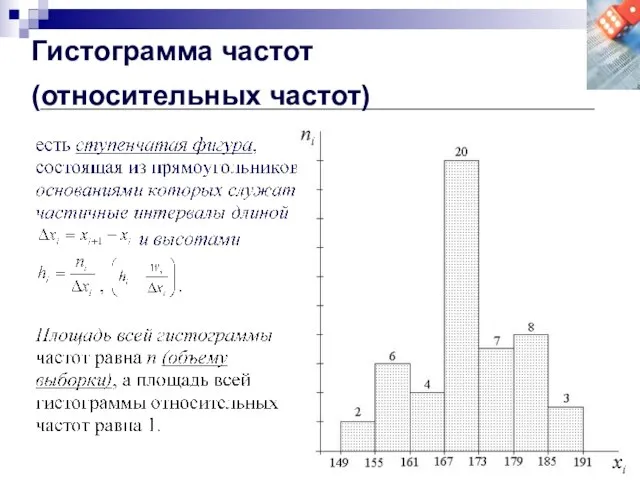
- 31. Гистограмма частот (относительных частот)
- 32. Эмпирическая функция распределения
- 33. Эмпирической функцией распределения (функцией распределения выборки) называется относительная частота события где – число вариант, меньших x
- 34. Теоретической функцией распределения называется функция распределения F(x) случайной величины X, вычисленная по генеральной совокупности, т.е., вероятность
- 35. При возрастании объема выборки различия между и уменьшаются.
- 36. теорема (Гливенко) При неограниченном возрастании объема выборки эмпирическая функция распределения сходится по вероятности к теоретической функции
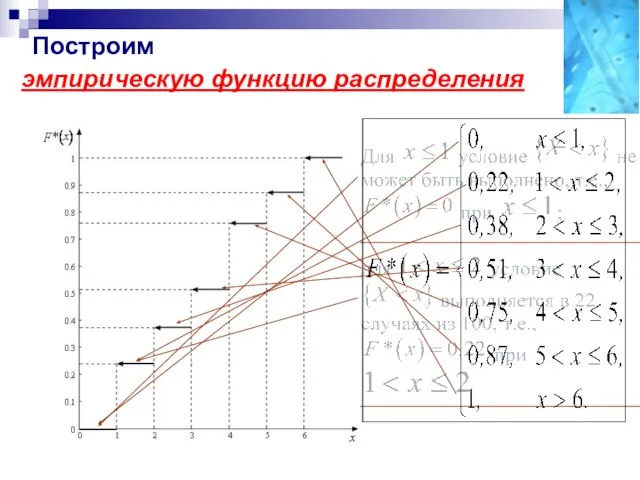
- 37. пример Построим эмпирическую функцию распределения для ранее рассмотренного примера (подбрасывание кости). Распределение приведено ниже.
- 38. Построим эмпирическую функцию распределения
- 39. Числовые характеристики статистического распределения выборки Пусть имеется генеральная совокупность объема N, из которой сделана выборка объема
- 40. Каждой числовой характеристике случайной величины ХГ соответствует ее выборочный аналог – характеристика случайной величины XВ. При
- 41. Выборочное среднее – среднее арифметическое значений выборки числовые характеристики выборки
- 42. Выборочное среднее – среднее арифметическое значений выборки числовые характеристики выборки
- 43. Выборочная мода – наиболее вероятное значение в выборке (варианта с наибольшей частотой). Выборочная медиана – значение
- 44. Выборочная дисперсия – среднее значение квадрата отклонения числовые характеристики выборки Эта формула может быть преобразована к
- 45. Выборочное среднее квадратическое отклонение Исправленная выборочная дисперсия Исправленное выборочное среднее квадратическое отклонение числовые характеристики выборки
- 46. Числовые характеристики генеральной совокупности Генеральное среднее – среднее арифметическое значений признака X генеральной совокупности:
- 47. Числовые характеристики генеральной совокупности Генеральная дисперсия – среднее по генеральной совокупности значение квадрата отклонения
- 48. Числовые характеристики генеральной совокупности Генеральное среднее квадратическое отклонение (стандартное отклонение )
- 49. В результате студент должен: владеть основными понятиями математической статистики; уметь преобразовывать выборочные данные к виду, удобному
- 51. Скачать презентацию











































 Числа - великаны
Числа - великаны Игра для 4 классов
Игра для 4 классов  Путешествие в сказку «Десятичные дроби» Повторение 5 класса
Путешествие в сказку «Десятичные дроби» Повторение 5 класса Презентация по математике "Тест по математике за первое полугодие для 1 класса" - скачать
Презентация по математике "Тест по математике за первое полугодие для 1 класса" - скачать  Счет
Счет Математика. Основы школьного стандарта
Математика. Основы школьного стандарта Деление натуральных чисел. Свойства деления. 5 класс
Деление натуральных чисел. Свойства деления. 5 класс Единицы объёма. Решение задач на нахождение объёма
Единицы объёма. Решение задач на нахождение объёма Осевая симметрия
Осевая симметрия Элементы теории матричных игр
Элементы теории матричных игр Задачи по математике
Задачи по математике Аттестационная работа. Рецензия на проектно-исследовательскую работу Виртуальные и реальные маршруты Казани
Аттестационная работа. Рецензия на проектно-исследовательскую работу Виртуальные и реальные маршруты Казани Высота треугольника ГБОУ СОШ №854 Разработано Учителем математики Филипповой Н.А.
Высота треугольника ГБОУ СОШ №854 Разработано Учителем математики Филипповой Н.А.  Определение параллельных прямых
Определение параллельных прямых Смежные и вертикальные углы
Смежные и вертикальные углы Презентация по математике "Золотое сечение и числа Фибоначи" - скачать
Презентация по математике "Золотое сечение и числа Фибоначи" - скачать  Презентация по математике "Килограмм" - скачать
Презентация по математике "Килограмм" - скачать  Скачать презентацию Пирамида
Скачать презентацию Пирамида  Сумма углов треугольника
Сумма углов треугольника Состав числа. Палочки Кюизенера
Состав числа. Палочки Кюизенера Числовые функции. Определение и способы задания
Числовые функции. Определение и способы задания Теорема Пифагора
Теорема Пифагора Применение метода рационализации при решении неравенств и систем неравенств
Применение метода рационализации при решении неравенств и систем неравенств Виды графов
Виды графов Геометрия. Картинки к уроку 4, М-2, часть 1
Геометрия. Картинки к уроку 4, М-2, часть 1 Сумма углов треугольника
Сумма углов треугольника Пределы функций. Понятие, основные определения, свойства, методы вычислений
Пределы функций. Понятие, основные определения, свойства, методы вычислений Решение квадратных уравнений. 8 класс
Решение квадратных уравнений. 8 класс