Содержание
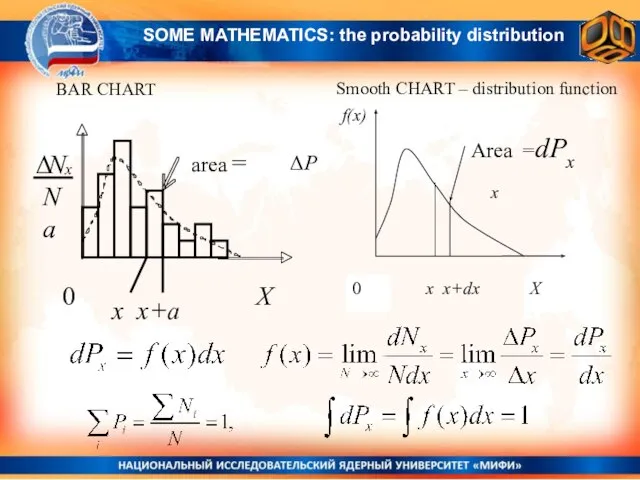
- 2. BAR CHART Smooth CHART – distribution function x x+a ΔP x SOME MATHEMATICS: the probability distribution
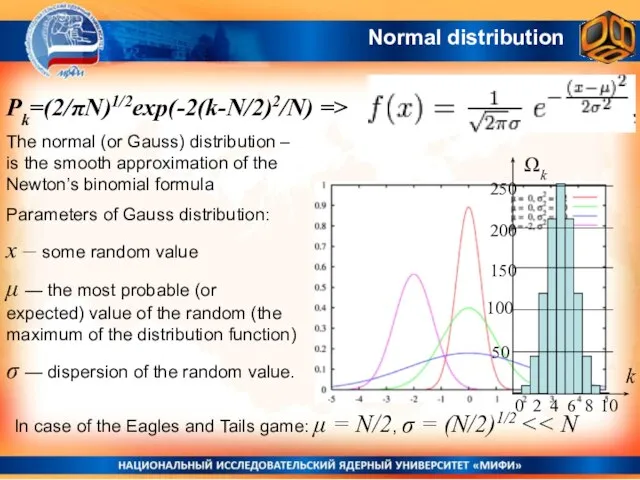
- 3. Normal distribution The normal (or Gauss) distribution – is the smooth approximation of the Newton’s binomial
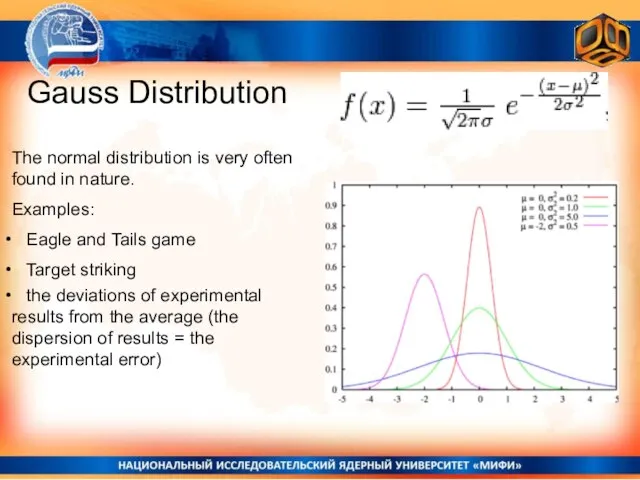
- 4. Gauss Distribution The normal distribution is very often found in nature. Examples: Eagle and Tails game
- 5. Statistical Entropy in Molecular Physics: the logarithm of the number of possible micro-realizations of a state
- 6. Entropy is the additive quantity. J/К Statistical Entropy in Physics. For the state of the molecular
- 7. Not a strict proof, but plausible considerations. ~ Statistical Entropy and the Entropy of Ideal Gas
- 8. ~ Statistical Entropy and the Entropy of Ideal Gas Ω~ VNTiN/2 /N!; S=k ln Ω =kNln(VTi/2/NC)=
- 9. The Distributions of Molecules over Velocities and Energies Maxwell and Boltzmann Distributions That will be the
- 10. If gas is in thermodynamic equilibrium state –the macroscopic parameters (temperature, pressure) are kept stable and
- 11. Each velocity vector can be presented as a point in the velocity space, As all the
- 12. The probability that the end of the 3-dimensional velocity vector V, will fir into the small
- 13. Noe some mathematics: We will calculate the derivative by dVx as Distribution of molecules over velocities
- 14. The only function which satisfies the equation: as well as the initial condition here α must
- 15. From normalization condition : we obtain: The Poisson integral: Distribution of molecules over velocities
- 16. THE PROPERTIES OF AVERAGES. Average of the sum of two values equals to the sum of
- 17. Probability Distribution and Average Values Examples: in case of even distribution of molecules over certain spherical
- 18. Different Kinds of Averages Y X Z V = = 3R/4 - average ( )1/2 =
- 19. The average of the squared velocity equals to: This integral once again can be reduced to
- 20. The basic assumption of thermodynamics (every degree of freedom accumulates the same energy): Distribution of molecules
- 21. The distribution over absolute values of velocities: , Distribution of molecules over velocities
- 22. Function defines the probability that velocity is within the “cubic” range: Probability to find the absolute
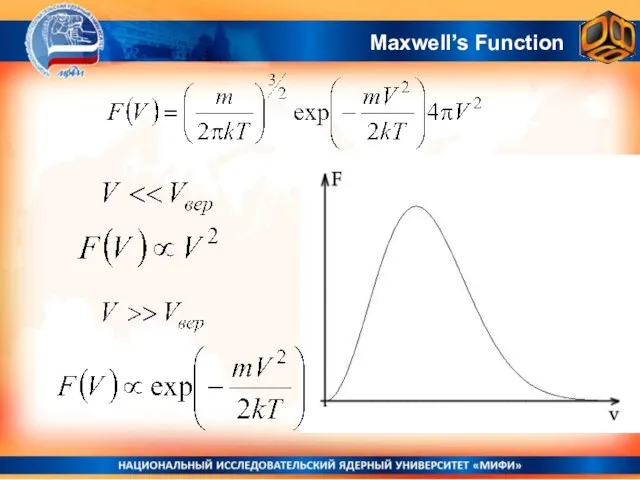
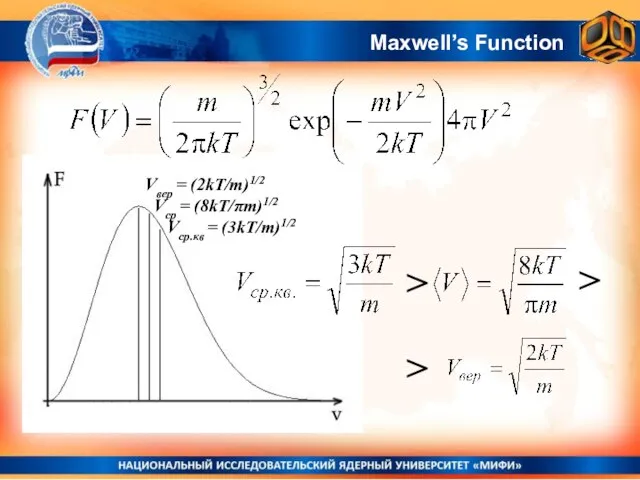
- 23. Maxwell’s Function
- 24. Area under the curve is always equal to 1 Maxwell’s Function
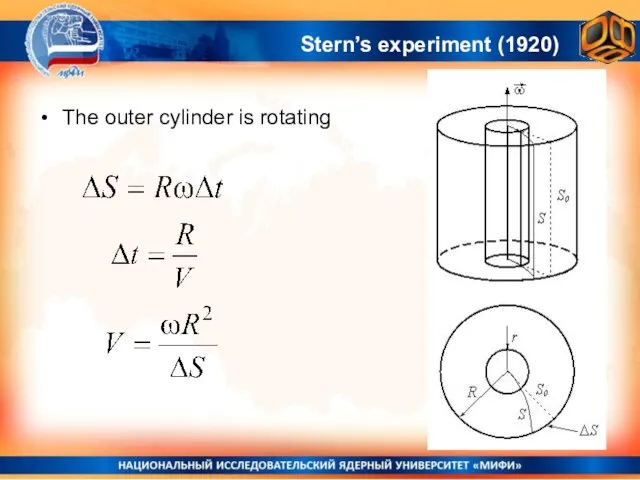
- 25. Stern’s experiment (1920) The outer cylinder is rotating
- 26. Lammert’s Experiment (1929) Two rotating discs with radial slots. One is rotating ahead of the other.
- 27. Most probable velocity. Most probable velocity corresponds to the maximum of the Maxwell’s function) Most probable
- 28. Average velocity. Average velocity by deffinition For Maxwell’s function:
- 29. Average squared velocity by definition Average squared velocity.
- 30. Most probable: Averge: Average squared: Three kinds of average velocities
- 31. Maxwell’s Function Vвер = (2kT/m)1/2 Vср = (8kT/πm)1/2 Vср.кв = (3kT/m)1/2 > > >
- 32. Example: Example: The mixture of oxygen and nitrogen (air) has the temperature T = 300 K.
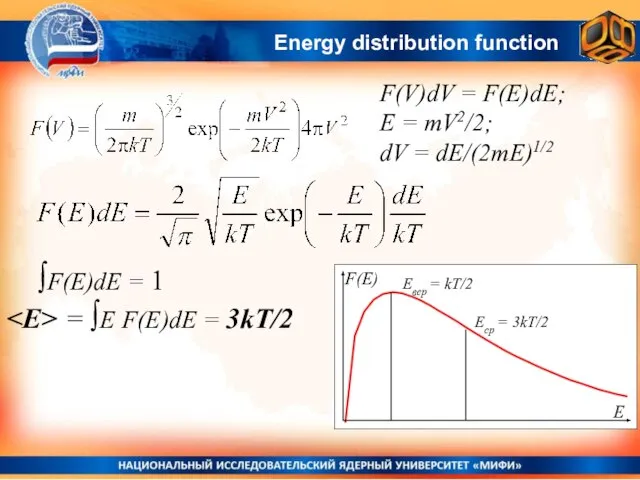
- 33. Energy distribution function F(V)dV = F(E)dE; E = mV2/2; dV = dE/(2mE)1/2 ∫F(E)dE = 1 =
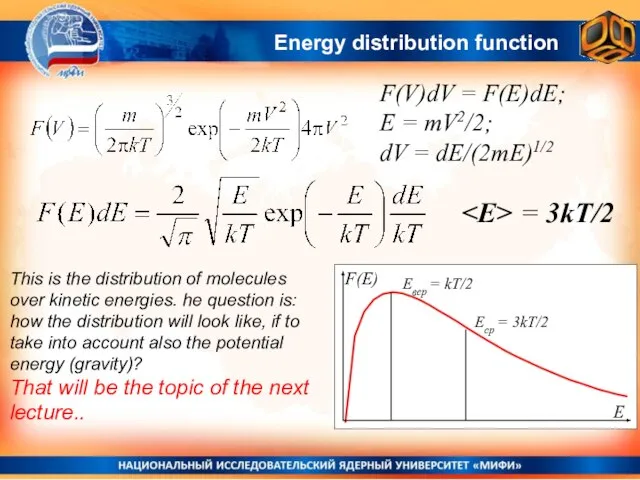
- 34. Energy distribution function F(V)dV = F(E)dE; E = mV2/2; dV = dE/(2mE)1/2 = 3kT/2 This is
- 36. Скачать презентацию

























 Комитет по народному образованию Администрации Солнечногорского муниципального района Муниципальное общеобразовательное учре
Комитет по народному образованию Администрации Солнечногорского муниципального района Муниципальное общеобразовательное учре Теория вероятностей. Треугольник Паскаля
Теория вероятностей. Треугольник Паскаля Логические основы модели Раша
Логические основы модели Раша Стереометрия в задачах ЕГЭ
Стереометрия в задачах ЕГЭ Использование интерактивных методов обучения как средство активизации познавательной деятельности обучающихся
Использование интерактивных методов обучения как средство активизации познавательной деятельности обучающихся  Работа по кафедре геометрии, мини-проект «Танграм»
Работа по кафедре геометрии, мини-проект «Танграм» Измерение углов
Измерение углов Ряд Фурье с произвольным периодом
Ряд Фурье с произвольным периодом Презентация по математике "Бизнес-игра" - скачать бесплатно
Презентация по математике "Бизнес-игра" - скачать бесплатно Modelagem Matemático Computacional FFI0321
Modelagem Matemático Computacional FFI0321 Геометрические преобразования
Геометрические преобразования Применение производной к нахождению наибольшего и наименьшего значения функции
Применение производной к нахождению наибольшего и наименьшего значения функции Перпендикулярные прямые
Перпендикулярные прямые История развития математики
История развития математики Задачи в УМК Г.К. Муравин, О.В.Муравина развивающие творческие способности учащихся
Задачи в УМК Г.К. Муравин, О.В.Муравина развивающие творческие способности учащихся Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения
Готовимся к ЕГЭ. Задача С2. Задачи, где присутствует построение сечения Свойства предметов (Занятие 2)
Свойства предметов (Занятие 2) Mixed strategy Nash equilibrium. (Lecture 3)
Mixed strategy Nash equilibrium. (Lecture 3) Средняя линия треугольника
Средняя линия треугольника Нахождение числа по его дроби
Нахождение числа по его дроби Задачи на построение
Задачи на построение Тема урока: Сложение и вычитание десятичных дробей Урок математики в 5 классе
Тема урока: Сложение и вычитание десятичных дробей Урок математики в 5 классе 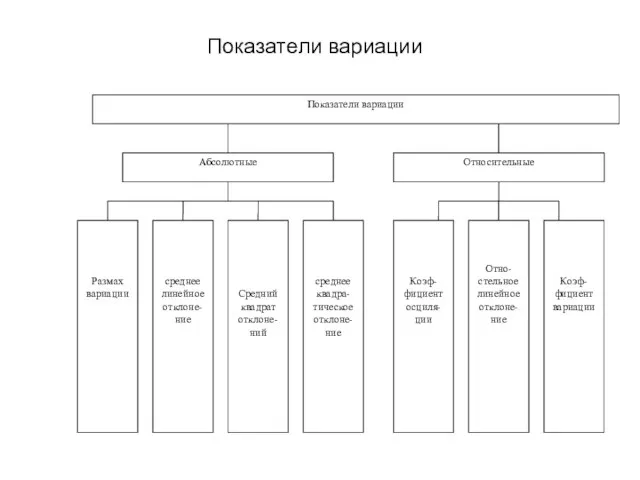 Показатели вариации
Показатели вариации Подібні трикутники
Подібні трикутники Презентация на тему Парабола
Презентация на тему Парабола Решение задач части С по планиметрии
Решение задач части С по планиметрии Математика 1кл. Работу выполнила Светлана Александровна.
Математика 1кл. Работу выполнила Светлана Александровна. Презентация по математике "Вычисление площадей с помощью интегралов" - скачать
Презентация по математике "Вычисление площадей с помощью интегралов" - скачать