Содержание
- 2. - Понятие натурального числа и нуля - Отношения «равно», «меньше», «больше» - Арифметические операции над числами
- 3. Определение целого неотрицательного числа
- 4. Математические понятия, как правило, проходят длительный путь исторического развития. Первоначально они возникают в процессе решения практических
- 5. При этом понятия не имеют еще строгих определений. Даются расплывчатые приблизительные пояснения, указания на наглядные представления.
- 6. Следующий этап в развитии математических понятий наступает, когда место наглядных рассмотрений занимают рассуждения, отличающиеся, однако, отсутствием
- 7. При аксиоматическом построении какой-нибудь теории поступают так: Выбирают некоторые объекты, изучаемые теорией, и некоторые отношения между
- 8. Вслед за основными понятиями и отношениями формулируются основные предложения, их называют аксиомами, которые в данной теории
- 9. Система аксиом должна быть: а) непротиворечивой, т.е. мы должны быть уверены, что делая всевозможные выводы из
- 10. Аксиоматическое определение натурального числа Как и все математические понятия, натуральные числа возникли из потребностей практики. Со
- 11. Наука, которая изучает числа и действия над ними, получила название «арифметика» - от греческого аrithmos -
- 12. Известными также считаются понятия множества и другие теоретико-множественные понятия, а также правила логики
- 13. Элемент, непосредственно следующий за элементом а, обозначается а´ Отношение «непосредственно следовать за» удовлетворяет следующим аксиомам:
- 17. Множество N, для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1- 4, называется множеством
- 18. Выбирая в качестве множества N некоторое конкретное множество, на котором задано конкретное отношение «непосредственно следовать за»,
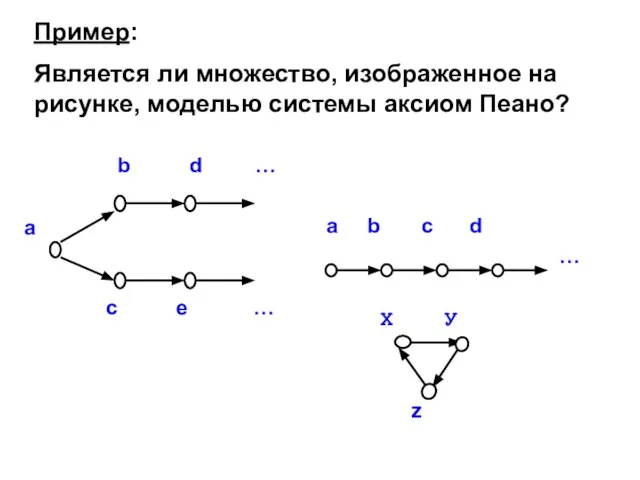
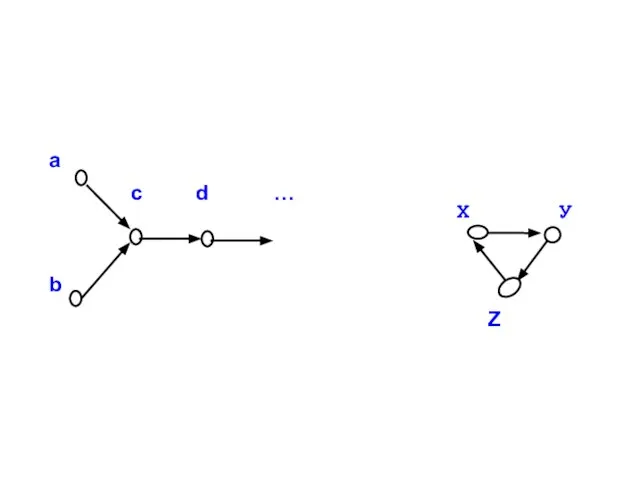
- 19. Пример: Является ли множество, изображенное на рисунке, моделью системы аксиом Пеано?
- 21. Отношение «непосредственно предшествовать» Если натуральное число b непосредственно следует за натуральным числом а, то число а
- 22. Множество целых неотрицательных чисел Обозначают Z0 или N0 N0 = N ∪ {0} 0, 1, 2,
- 23. Те свойства отношения «непосредственно следовать за, которые отражены в аксиомах 1 – 4, изучаются в начальных
- 24. Каждое новое число с самого начала выступает как продолжение ранее изученного отрезка натурального ряда чисел. Любое
- 25. Упражнения. Покажите, что множество целых неотрицательных чисел является моделью системы аксиом Пеано. Какое число выполняет при
- 27. Счет Порядковые и количественные натуральные числа Теоретико-множественный подход
- 28. 1 2 3 4 5 6
- 29. Требования, соблюдаемые при счете: первому отмеченному предмету ставится в соответствие число 1; каждый раз отмечается предмет
- 30. Сущность счета заключается в установлении взаимно однозначного соответствия между множествами, подлежащими счету, и некоторым отрезком натурального
- 31. Отрезком Nа натурального ряда называется множество натуральных чисел, не превосходящих натурального числа а Nа = {х
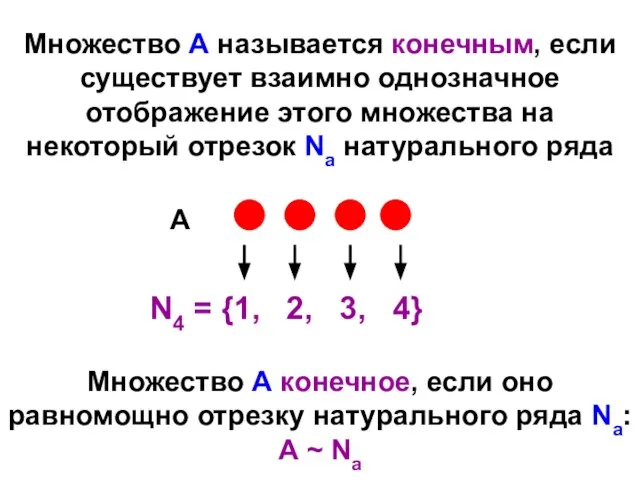
- 32. Множество А называется конечным, если существует взаимно однозначное отображение этого множества на некоторый отрезок Nа натурального
- 33. Множество А равномощно только одному отрезку натурального ряда Nа, и поэтому множеству А может быть поставлено
- 34. Пример: Множество А = {а, b, с} можно взаимно однозначно отобразить на отрезок натурального ряда N3.
- 35. Существует много нумераций одного и того же множества: b → 1 c → 2 a →
- 36. При пересчете элементы конечного множества расставляются в определенном порядке, а также устанавливается, сколько элементов содержит множество.
- 37. Определение С теоретико-множественных позиций натуральное число рассматривается как число элементов конечного множества n(∅) = 0
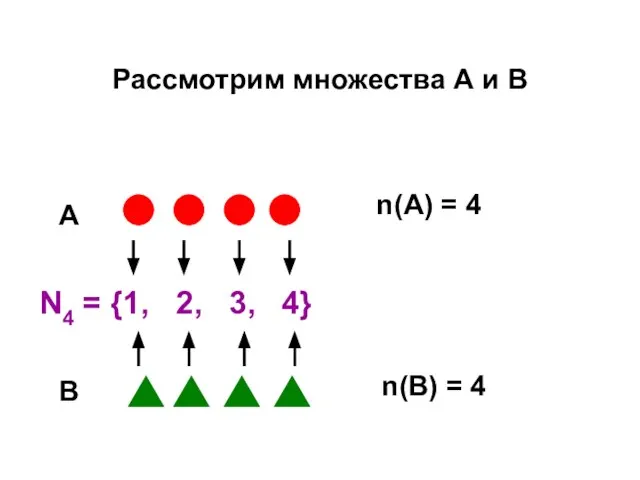
- 38. Рассмотрим множества А и В N4 = {1, 2, 3, 4} n(А) = 4 n(В) =
- 39. Следующие предложения равносильны: - Множествам А и В соответствует одно и то же число а -
- 40. Так как одному и тому же конечному множеству может соответствовать лишь одно натуральное число а, то
- 41. Количественное натуральное число рассматривается как общее свойство класса конечных равномощных множеств
- 42. Упражнения 1) Запишите все элементы множества: N7, N11, N14. 2) Какие из указанных ниже множеств являются
- 43. 5) Приведите примеры класса множеств, соответствующих натуральному числу: а) 5, б) 10, в)12. 6) При знакомстве
- 44. 9) Докажите, что множество А – конечное, если: а) А – множество букв в слове «параллелограмм»;
- 45. Натуральное число как результат измерения величин Натуральные числа используют не только для пересчета элементов конечных множеств,
- 46. Считают, что отрезок а разбит на отрезки (состоит из отрезков) а1, а2, …, аn, если он
- 47. Выберем из множества отрезков некоторый отрезок е и назовем его единичным отрезком или единицей длины Если
- 48. mе1(а) = 12 или а = 12 е1 mе2(а) = 6 или а = 6 е2
- 49. Натуральное число как мера отрезка а показывает, из скольких выбранных единичных отрезков е состоит отрезок а
- 50. Натуральное число – это элемент множества Ν, на котором задано отношение «непосредственно следовать за», удовлетворяющее 4-м
- 52. Скачать презентацию












































 Теоретические основы метрологии. Аппроксимация градуировочных характеристик измерительных преобразователей. (Лекция 2)
Теоретические основы метрологии. Аппроксимация градуировочных характеристик измерительных преобразователей. (Лекция 2) Решение линейных уравнений с одной переменной
Решение линейных уравнений с одной переменной Решение показательного уравнения
Решение показательного уравнения Презентация по математике Признаки делимости чисел
Презентация по математике Признаки делимости чисел  Тема: «Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых»
Тема: «Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых»  Десятичная система счисления
Десятичная система счисления Нахождение разности двух чисел
Нахождение разности двух чисел Фигура цилиндр
Фигура цилиндр Математическая игра «Звёздный час» 9 класс
Математическая игра «Звёздный час» 9 класс Внетабличное деление двузначного числа на однозначное
Внетабличное деление двузначного числа на однозначное Знакомство с понятием ЗАДАЧА 1 класс
Знакомство с понятием ЗАДАЧА 1 класс Квадратичная функция
Квадратичная функция Визначні математичні задачі
Визначні математичні задачі Собственные значения и собственные векторы матрицы
Собственные значения и собственные векторы матрицы Исторические задачи по математике
Исторические задачи по математике Великая теорема Ферма
Великая теорема Ферма Системы линейных дифференциальных уравнений
Системы линейных дифференциальных уравнений Обыкновенные дроби и их применение
Обыкновенные дроби и их применение Градиентный бустинг
Градиентный бустинг Теорема Пифагора
Теорема Пифагора טופולוגיה - תרגול 3
טופולוגיה - תרגול 3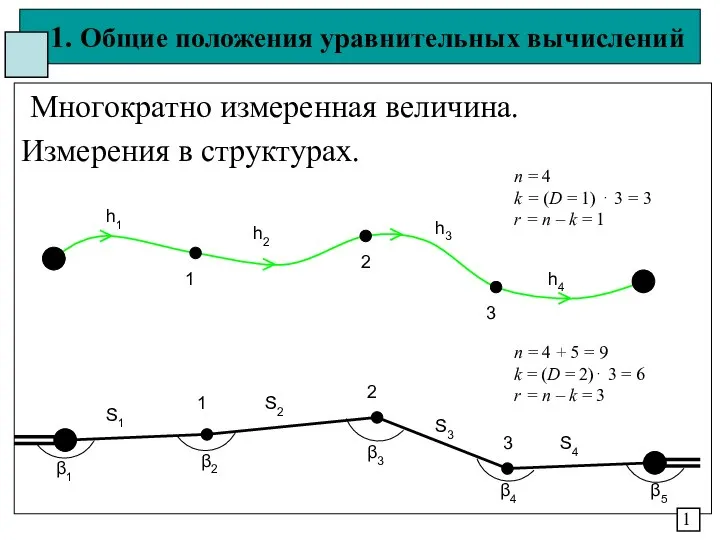 Общие положения уравнительных вычислений. Многократно измеренная величина. Измерения в структурах
Общие положения уравнительных вычислений. Многократно измеренная величина. Измерения в структурах Урок математики. (Часть 1. 1 класс)
Урок математики. (Часть 1. 1 класс) Combinational logic design
Combinational logic design Параллельные прямые
Параллельные прямые Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой Иррациональные уравнения
Иррациональные уравнения Введение и история появления бустинга
Введение и история появления бустинга