Содержание
- 2. Цели урока: познакомить учащихся с новым видом уравнения с одной переменной; изучить и закрепить способ решения
- 3. Методы решения целых уравнений: Р(х)=0, где Р(х) – многочлен стандартного вида. 1. Разложение левой части на
- 4. Уравнения, степень которых выше двух, иногда удается решить, введя новую переменную. Повторим примеры решения уравнений этим
- 5. Ответы: Куб. Дискриминант. Корень. Равносильное. Уравнение. Приведённое. Трёхчлен. Формула. Виет. Коэффициент. Неполное. Решение.
- 6. Биквадратные уравнения
- 7. Алгоритм решения биквадратного уравнения: Ввести замену переменной: пусть х2=t; Составить квадратное уравнение с новой переменной аt2+вt+с=0;
- 8. Метод введения новой переменной позволяет легко решать уравнения четвёртой степени, имеющие вид ах4+вх2+с=0. Уравнения вида ах4+вх2+с=0,
- 9. Ответы к самостоятельной работе. В-1: Не имеет корней. х1=1; х2=-1. х=0. В-2: Не имеет корней. х1=1;
- 10. Домашнее задание: Стр. 64, пункт 11, выучить правило, разноуровневые карточки.
- 12. Скачать презентацию









 Обратные функции. 10 класс
Обратные функции. 10 класс Аттестационная работа. Обучение математике на основе моделей вариативных образовательных маршрутов
Аттестационная работа. Обучение математике на основе моделей вариативных образовательных маршрутов Иррациональные уравнения Урок 81
Иррациональные уравнения Урок 81 Многогранники, описанные около сферы
Многогранники, описанные около сферы Простые числа. Леонард Эйлер
Простые числа. Леонард Эйлер Численные методы алгебры
Численные методы алгебры Зарождение алгебры
Зарождение алгебры Тождества. Тождественные преобразования выражений
Тождества. Тождественные преобразования выражений Математика в сказках
Математика в сказках Кто хочет стать отличником
Кто хочет стать отличником Умножение и деление дробей
Умножение и деление дробей Десятичные дроби
Десятичные дроби Эволюция, или как превратить линейную модель в искусство
Эволюция, или как превратить линейную модель в искусство Многоугольники в жизни
Многоугольники в жизни Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Презентация на тему Медицина и математика
Презентация на тему Медицина и математика 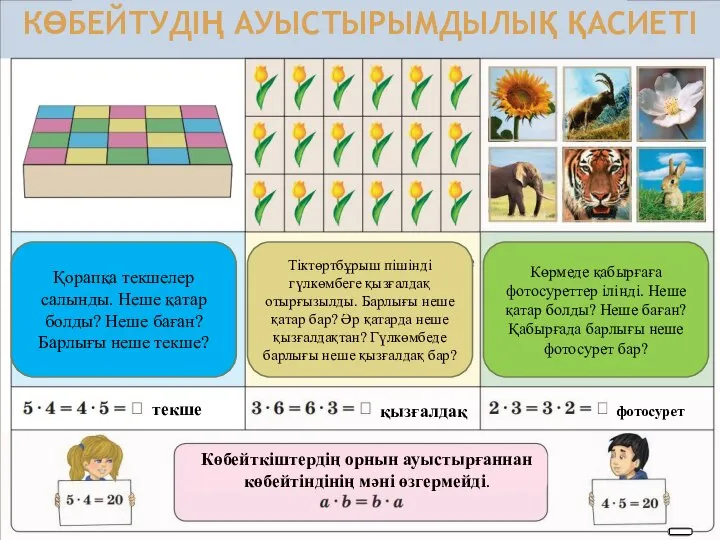 Көбейтудің ауыстырымдылық қасиеті
Көбейтудің ауыстырымдылық қасиеті Умножение десятичных дробей
Умножение десятичных дробей Кеңістіктегі параллель түзулер
Кеңістіктегі параллель түзулер Умножение дробей. 6 класс
Умножение дробей. 6 класс Упрощение выражений
Упрощение выражений Объемы и площади. Куб
Объемы и площади. Куб Неделя математики. Открытая неделя - 2020
Неделя математики. Открытая неделя - 2020 Гомотетия. Гомотетичные фигуры
Гомотетия. Гомотетичные фигуры Математика – білім негізі
Математика – білім негізі Математический кроссворд
Математический кроссворд Решение задач. Теорема Пифагора
Решение задач. Теорема Пифагора Умножение десятичных дробей на натуральное число
Умножение десятичных дробей на натуральное число