Содержание
- 2. Два уравнения f₁(x)= g₁(x) и f₂(x)= g₂(x) называются равносильными, если множества их корней совпадают. Уравнения f₂(x)=
- 3. Процесс преобразования любого уравнения можно записать так: (1)→(2)→(3)→(4)→… Это значит, что заданное уравнение (1) преобразуют в
- 4. Решения уравнения осуществляется по следующему плану: 1)Техническая часть, т.е. осуществление цепочки превращений по схеме: (1)→(2)→(3)→(4)→… и
- 5. При осуществлении данного плана возникают 4 вопроса: 1) Как узнать, является ли переход от одного уравнения
- 6. Начнем с 1 вопроса. Есть 3 теоремы – назовём их «спокойные», которые всегда «работают» и не
- 7. И есть 3 «беспокойные» теоремы, которые выполняются только в определенных условиях, и поэтому требуют внимания от
- 8. Теперь мы можем ответить на 2 вопроса: если в процессе решения уравнения применялась одна из теорем-4
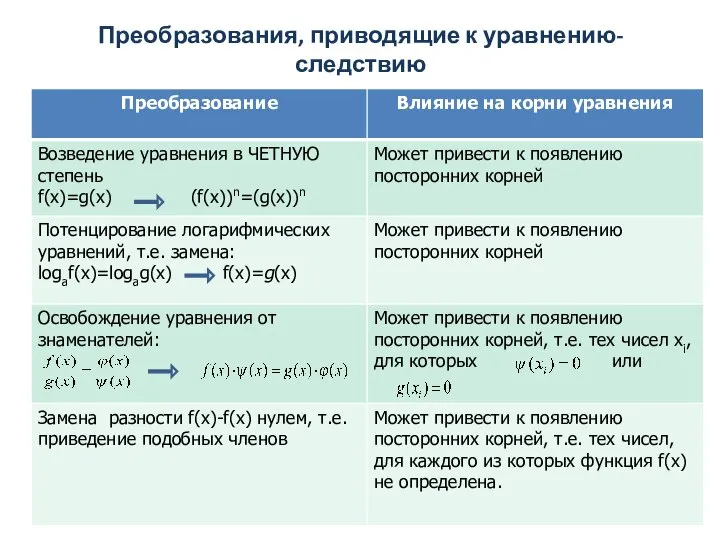
- 9. Преобразования, приводящие к уравнению-следствию
- 10. Если при решении данного уравнения совершен переход к уравнению-следствию, то необходимо проверить, все ли корни уравнения
- 11. №8.22 (а) Решите уравнение: 1) 2) № 8.23(а)
- 12. №8.24 (а,в) Решите уравнение: 1) 2)
- 13. №8.25 (а,в) Решите уравнение: 1) 2)
- 14. №8.28 (а,в) Решите уравнение: 1) 2)
- 16. Скачать презентацию












 Работа учителя математики Сиверской гимназии Скрылёвой Татьяны Леонидовны _
Работа учителя математики Сиверской гимназии Скрылёвой Татьяны Леонидовны _ Умножение и деление степеней. Закономерности
Умножение и деление степеней. Закономерности Метод растянутых координат. (Лекция 9)
Метод растянутых координат. (Лекция 9) Презентация по математике "ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015" - скачать бесплатно
Презентация по математике "ТРЕНАЖЕРЫ ПО МАТЕМАТИКЕ ДЛЯ ПОДГОТОВКИ К ЕГЭ 2015" - скачать бесплатно Функция y=x^n
Функция y=x^n Окружность и ее элементы. Замечательные линии окружности
Окружность и ее элементы. Замечательные линии окружности Степень числа. Квадрат и куб числа
Степень числа. Квадрат и куб числа Теория кривых. Сопровождающий трехранник
Теория кривых. Сопровождающий трехранник Метод координат
Метод координат Смешанные дроби. 5 класс
Смешанные дроби. 5 класс Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Формирование обобщенных многокритериальных оценок
Формирование обобщенных многокритериальных оценок Длина ломаной
Длина ломаной Арифметические диктанты
Арифметические диктанты Вычисления буквенных выражений. Алгебра 7 класс
Вычисления буквенных выражений. Алгебра 7 класс Статистика. Необходимость возникновения статистики-науки
Статистика. Необходимость возникновения статистики-науки Динамика полета. Характерные скорости горизонтального полета самолета. (Лекция 6)
Динамика полета. Характерные скорости горизонтального полета самолета. (Лекция 6) Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Техника расчёта квадратов целых чисел
Техника расчёта квадратов целых чисел Краткие теоретические сведения. Планиметрия
Краткие теоретические сведения. Планиметрия Таблицы, часть 2, 9-11 классы
Таблицы, часть 2, 9-11 классы Числа от 1 до 100. Сложение и вычитание
Числа от 1 до 100. Сложение и вычитание Многогранники, описанные около сферы
Многогранники, описанные около сферы Единицы времени
Единицы времени Аrcsin
Аrcsin Компьютерное моделирование как метод научного познания
Компьютерное моделирование как метод научного познания Математика – это сила!
Математика – это сила!