Содержание
- 2. Понятие вектора Многие физические величины,например,сила,перемещение материальной точки,скорость,характеризуется не только своим числовым значением,но и направлением в пространстве.Такие
- 3. Вектор в геометрии В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано,
- 4. Рассмотрим произвольный отрезок.Его концы также граничными точками отрезка. На отрезке можно указать 2 направления: от одной
- 5. Любая точка плоскости также является вектором.В этом случае вектор называется нулевым.Начало нулевого вектора совпадает с его
- 6. Равенство векторов Векторы называются равными,если они сонаправлены и их длины равны.
- 7. Коллинеарность векторов. Ненулевые векторы называются коллинеарными, если они лежат оба на одной прямой,либо на параллельных прямых;
- 8. Противоположно направленные и сонаправленные векторы. Если 2 нулевых вектора a и b коллинеарны, то они могут
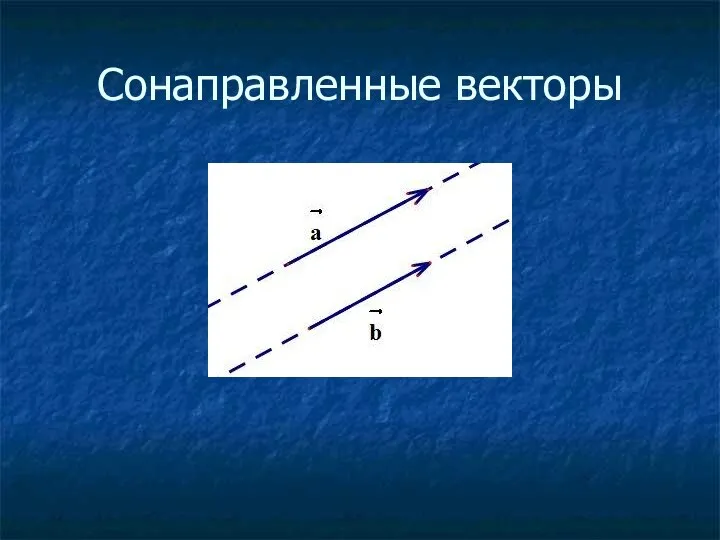
- 9. Сонаправленные векторы
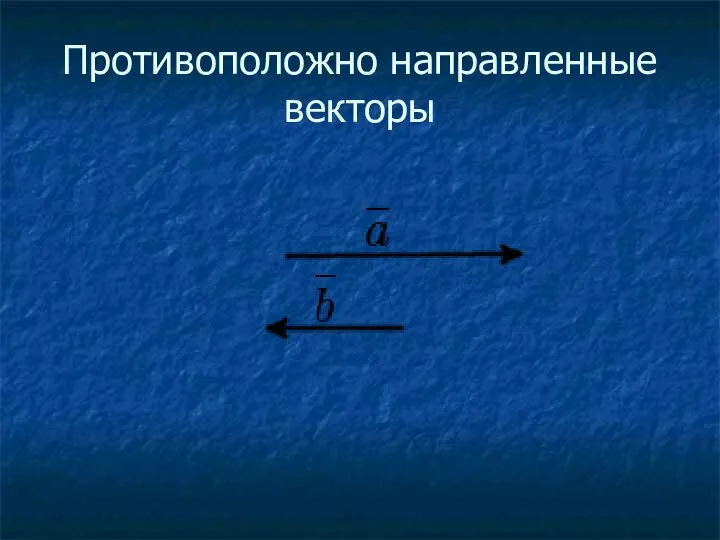
- 10. Противоположно направленные векторы
- 11. Сложение векторов Чтобы сложить 2 вектора- надо сложить их соответвующие координаты.
- 12. Разность векторов Чтобы вычеть один вектор из другого- надо вычесть соответствующие координаты первого вектора из второго
- 13. Модуль суммы векторов Модуль суммы двух векторов можно вычислить, используя теорему косинусов: Где cos {a},{b} —
- 14. Модуль разности векторов
- 15. Умножение вектора на число Умножение вектора a на число alpha >0, даёт сонаправленный вектор с длиной
- 16. Скалярное произведение вектора
- 17. Для геометрических векторов скалярное произведение определяется через их геометрические характеристики и вводится следующим образом: Здесь для
- 19. Скачать презентацию














 Нахождение дроби от числа и числа по его дроби
Нахождение дроби от числа и числа по его дроби Умножение вектора на число
Умножение вектора на число Перпендикуляр к прямой
Перпендикуляр к прямой Степенная функция. 10 класс
Степенная функция. 10 класс Чотирикутники
Чотирикутники Теория оптимизации
Теория оптимизации Алгебра высказываний при решении логических задач. Дизъюнктивные нормальные формы Лекция 3
Алгебра высказываний при решении логических задач. Дизъюнктивные нормальные формы Лекция 3 Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве
Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве Юбилейный ЕГЭ по математике «Вперед! Только вперед!»
Юбилейный ЕГЭ по математике «Вперед! Только вперед!» «Преданья старины далёкой» (Решение старинных задач) Южакова Елизавета 8 класс МОУ Новолялинская СОШ №4
«Преданья старины далёкой» (Решение старинных задач) Южакова Елизавета 8 класс МОУ Новолялинская СОШ №4 Қалдықпен бөлу
Қалдықпен бөлу Устная и письменная нумерация чисел в пределах 1000
Устная и письменная нумерация чисел в пределах 1000 Математическая викторина
Математическая викторина Сбор и группировка статистических данных
Сбор и группировка статистических данных МАТЕМАТИЧЕСКОЕ СТИХОТВОРЕНИЕ Сочинила: ученица 5 а класса ТЕТЮШЕВА АЛЕКСАНДРА МОУ СОШ с. Верхний Ломов Нижнеломовского района
МАТЕМАТИЧЕСКОЕ СТИХОТВОРЕНИЕ Сочинила: ученица 5 а класса ТЕТЮШЕВА АЛЕКСАНДРА МОУ СОШ с. Верхний Ломов Нижнеломовского района  ДЗ Математика 28.01.2021
ДЗ Математика 28.01.2021 Таблица умножения и деления на 5
Таблица умножения и деления на 5 Презентация по математике "Сложение и вычитание чисел." - скачать бесплатно_
Презентация по математике "Сложение и вычитание чисел." - скачать бесплатно_ Б Р Е Й Н – Р И Н Г
Б Р Е Й Н – Р И Н Г Умножение и деление дробных чисел 6 класс МАОУ СОШ №10 г.Краснокамска Минина Т.А.
Умножение и деление дробных чисел 6 класс МАОУ СОШ №10 г.Краснокамска Минина Т.А.  Пирамида – это многогранник, составленный из n-угольника
Пирамида – это многогранник, составленный из n-угольника Равновеликие многоугольники
Равновеликие многоугольники Своя игра. Действия с десятичными дробями
Своя игра. Действия с десятичными дробями Застосування похідної в різних областях науки
Застосування похідної в різних областях науки Квадрат суммы и разности
Квадрат суммы и разности Угол поворота. Радианная мера угла
Угол поворота. Радианная мера угла Интересные факты из математики
Интересные факты из математики Координатная плоскость
Координатная плоскость