Содержание
- 2. План занятия: Введение в теорию множеств Описание множеств Операции над множествами Примеры множеств Введение в математическую
- 3. Любая научная дисциплина требует теории для её изучения. Для математического анализа и для любой другой математической
- 4. Свойства любой научной теории Теорию невозможно доказать или опровергнуть: это набор аксиом, инструмент Любая теория, состоящая
- 5. То есть рано или поздно любая теория приводит к противоречиям внутри себя, что требует развития новой
- 6. Теория множеств
- 7. Теория множеств Топливом для развития теории множеств послужила необходимость исследования бесконечности, главным образом, исследование простых чисел
- 8. Понятие множества принадлежит к числу простейших математических понятий и не имеет точного определения. Любое множество задается
- 9. Описание множеств Теория множеств Множество обозначают заглавными латинскими буквами (A) Его элементы строчными латинскими буквами (a)
- 10. Описание множеств Теория множеств Множество обозначают заглавными латинскими буквами (A) Его элементы строчными латинскими буквами (a)
- 11. Множество натуральных чисел можно задать так: Множество целых чисел можно задать так: Множество рациональных чисел можно
- 12. Можно ли описать множество четных и нечетных чисел? Теория множеств
- 13. Можно ли описать множество четных и нечетных чисел? Теория множеств {2n | n∈Z}={...,-4,-2,0,2,4,6,...} {2n+1 | n∈Z}={...,-3,-1,1,3,5,...}
- 14. Можно ли описать множество простых чисел? Теория множеств
- 15. Можно ли описать множество простых чисел? Теория множеств Нет
- 16. Примеры множеств Примеры множеств
- 17. Множество вещественных чисел: R – числовая ось. (помимо рациональных чисел включает числа, которые нельзя представить в
- 18. где — мнимая единица. Примеры множеств Комплексные числа:
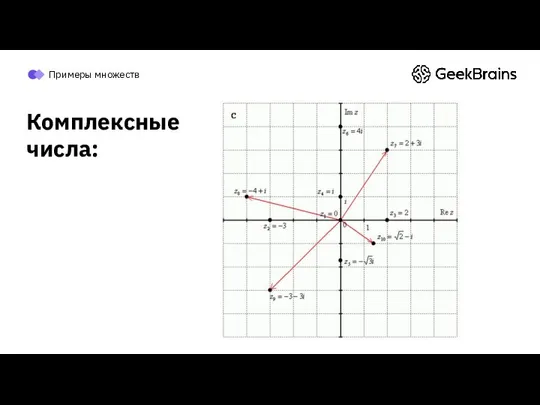
- 19. где — мнимая единица. Примеры множеств Re - real Im - imaginary Re Im Комплексные числа:
- 20. Примеры множеств Комплексные числа:
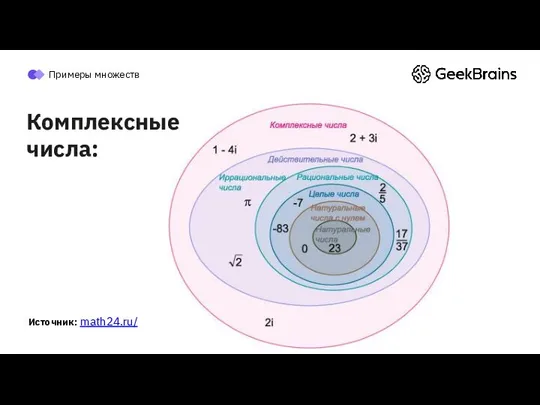
- 21. Источник: math24.ru/ Примеры множеств Комплексные числа:
- 22. Два множества равны тогда и только тогда, когда состоят из одних и тех же элементов. Если
- 23. В рамках рассматриваемой математической теории вводят два исключительных множества: Пустое множество (∅) , не содержащее элементов
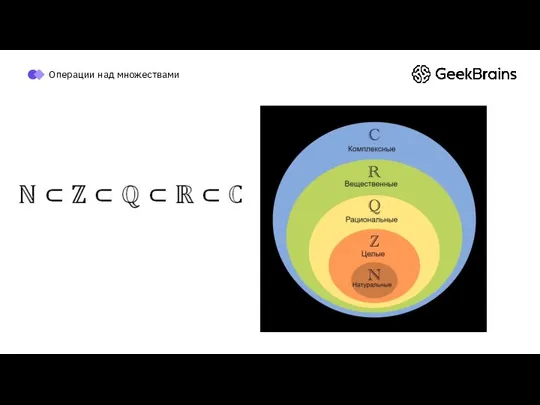
- 24. Операции над множествами Операции над множествами
- 25. Дополнение. Для любого множества ?⊂? определим дополнение Например, в множестве вещественных чисел дополнением к множеству ℚ
- 26. Объединение. Для любых двух множеств ?,?⊂? определим объединение Значок ∨ внутри фигурной скобки называется "дизъюнкция" ,
- 27. Пересечение. Для любых двух множеств ?,?⊂? определим пересечение Значок ∧ внутри фигурной скобки называется "конъюнкция", по
- 28. Разность. Для любых двух множеств ?,?⊂? определим разность Например, разность отрезков [1,3] и [2,7] является отрезок
- 29. Симметрическая разность. Для любых двух множеств ?,?⊂? определим симметрическую разность Значок ⊕ внутри фигурной скобки имеет
- 30. Реализация на Python Операции над множествами
- 31. Операции над множествами Реализация на Python
- 32. Операции над множествами
- 33. Множества. Рациональные числа Множества. Рациональные числа
- 34. Множества. Рациональные числа
- 35. Множества. Рациональные числа
- 36. Множества. Рациональные числа
- 37. Множества. Рациональные числа
- 38. Множества. Рациональные числа
- 39. Множества. Рациональные числа
- 40. Математическая логика Математическая логика
- 41. Математическая логика Логика высказываний рассматривает и решает вопрос об истинности или ложности высказываний на основе изучения
- 42. Высказыванием называется повествовательное предложение, про которое всегда определенно можно сказать, является оно истинным (1) или ложным
- 43. Математическая логика Пример 1. Предложение «Сдать зачет по математике можно, зная блестяще теорию или решив все
- 44. Способы работы с выражениями С помощью таблицы истинности. С помощью основных законов логики высказываний. Математическая логика
- 45. Логические операции и таблицы истинности Теория множеств
- 46. Логические операции и таблицы истинности Таблица истинности для конъюнкции (логическое умножение) A⋂B и
- 47. Логические операции и таблицы истинности Таблица истинности для дизъюнкции A⋃B или
- 48. Логические операции и таблицы истинности Логическое отрицание или инверсия: Ā К исходному логическому выражению добавляется частица
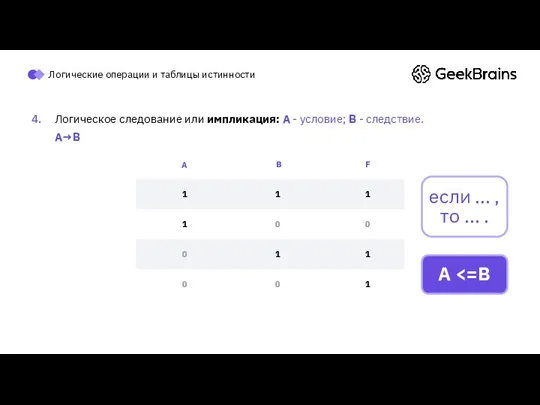
- 49. Логические операции и таблицы истинности Логическое следование или импликация: A - условие; B - следствие. A→B
- 50. Логические операции и таблицы истинности Логическое следование или импликация: A - условие; B - следствие. A→B
- 51. Логические операции и таблицы истинности Логическая равнозначность или эквивалентность: A↔B тогда и только тогда
- 52. Логические операции и таблицы истинности Логическая равнозначность или эквивалентность: A↔B A = B тогда и только
- 53. Логические операции и таблицы истинности Исключающее или: A ⊕ B
- 54. Логические операции и таблицы истинности Исключающее или: A ⊕ B A != B
- 55. Пример 2. Предложение «Если Сувар или Таиф проиграют, а Феникс выиграет тендер, то Альбатрос упрочит свое
- 56. Если истинное значение простых переменных P, Q, R, D, C соответственно равны “И”, “Л”, “Л”, “И”,
- 57. Таблица истинности Логические операции и таблицы истинности Пример 3. Доказать, что при любых значениях P и
- 58. Свойства и признаки Свойства и признаки
- 59. Свойства и признаки Когда учительница ругала Дениса за плохой почерк, он сказал: "У всех великих людей
- 60. Свойства и признаки Когда учительница ругала Дениса за плохой почерк, он сказал: "У всех великих людей
- 61. Свойства и признаки Предпосылка Дениса: «У всех великих людей был плохой почерк» (этому пока верим; разбираемся,
- 62. Свойства и признаки Если человек великий (А) У него плохой почерк (B) Согласно утверждению Дениса, плохой
- 63. Свойства и признаки Можно привести много верных математических утверждений, обратные к которым неверны. Например: если два
- 64. Законы логики высказываний Коммутативность конъюнкции: A ⋂ B = B ⋂ A Коммутативность дизъюнкции: A ⋃
- 65. Закон де Моргана относительно конъюнкции: (A ⋂ B) = Ā ⋃ B Закон де Моргана относительно
- 66. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 67. Законы логики высказываний Дистрибутивность дизъюнкции относительно конъюнкции: A ⋃ (B ⋂ C) = (A ⋃ B)
- 68. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 69. Законы логики высказываний Закон де Моргана относительно конъюнкции: (A ⋂ B) = Ā ⋃ B Закон
- 70. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 71. Законы логики высказываний Закон поглощения конъюнкции: A ⋂ (A ⋃ B) = A A ⋂ “Л”
- 72. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 73. Законы логики высказываний Ассоциативность дизъюнкции: A ⋃ (B ⋃ C) = (A ⋃ B) ⋃ C
- 74. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 75. Законы логики высказываний Закон исключения третьего: A ⋃ Ā = “И”
- 76. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 77. Законы логики высказываний A ⋃ “Л” = A, A ⋃ “И” = “И”
- 78. Законы логики высказываний Пример 4. Упростить высказывание: (A ⋃ (A ⋂ B)) ⋃ (A ⋃ (C
- 79. Кванторы Высказывания с кванторами Всеобщности (∀) (читается «для любого») Существования (∃) (читается «существует»)
- 80. Отрицания высказываний Высказывания с кванторами
- 81. Пример построения отрицания Высказывания с кванторами
- 82. Квантор меняется на противоположный (∀↔∃). Принадлежность множеству сохраняется. Перед логическим сказуемым ставится «не». Пример построения отрицания
- 83. Пара интересных примеров на логику Пример 1 За книгу заплатили 100р. и еще половину своей стоимости.
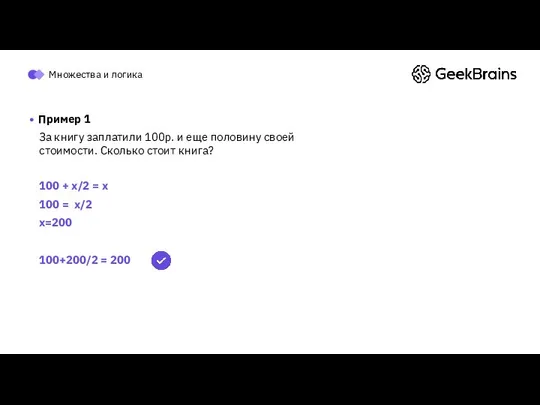
- 84. Пример 1 За книгу заплатили 100р. и еще половину своей стоимости. Сколько стоит книга? 100 +
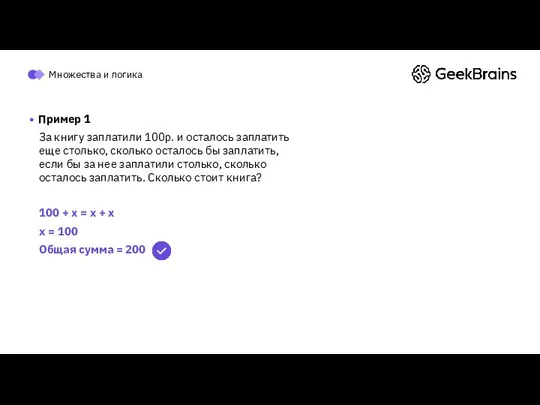
- 85. Пример 2 За книгу заплатили 100р. и осталось заплатить еще столько, сколько осталось бы заплатить, если
- 86. Пример 1 За книгу заплатили 100р. и осталось заплатить еще столько, сколько осталось бы заплатить, если
- 87. И еще пример! Рыцари всегда говорят правду, а лжецы всегда лгут. Представьте, что все лжецы острова
- 88. И еще пример! Рыцари всегда говорят правду, а лжецы всегда лгут. Представьте, что все лжецы острова
- 89. Спасибо Множества и логика
- 90. Про домашнее задание Как надо: Множества и логика
- 92. Скачать презентацию



















































































 Проценты. 9 класс (для учащихся школ VIII вида)
Проценты. 9 класс (для учащихся школ VIII вида) Сonstructive problems on divisibility, prime and composite numbers
Сonstructive problems on divisibility, prime and composite numbers Алгоритм вычисления площадей
Алгоритм вычисления площадей Нелинейная регрессия
Нелинейная регрессия Звездчатые многогранники
Звездчатые многогранники Презентация по математике "Сравнение чисел. Графы" - скачать бесплатно
Презентация по математике "Сравнение чисел. Графы" - скачать бесплатно Практическое применение теоремы Пифагора
Практическое применение теоремы Пифагора Готовимся к ВПР. Математика. 1-4 класс
Готовимся к ВПР. Математика. 1-4 класс Первообразная
Первообразная Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации
Преподавание элементов теории вероятности и статистики в 5-9 классах. Система подготовки учащихся к итоговой аттестации Thanksgiving
Thanksgiving Гоночная трасса, как пример мультиграфа
Гоночная трасса, как пример мультиграфа Презентация по математике "Интеллектуальная игра Что? Где? Когда?" - скачать
Презентация по математике "Интеллектуальная игра Что? Где? Когда?" - скачать  Формулы сокращённого умножения (часть 1)
Формулы сокращённого умножения (часть 1) Задачи на движение
Задачи на движение Лабораторная работа
Лабораторная работа Геометрический смысл производной
Геометрический смысл производной Екіфакторлы дисперсиялық талдау
Екіфакторлы дисперсиялық талдау Проецирование прямой
Проецирование прямой Конструктивные описания графов и их приложения
Конструктивные описания графов и их приложения Цена набора товаров
Цена набора товаров Раскрытие скобок
Раскрытие скобок Численное решение систем линейных алгебраических уравнений (СЛАУ)
Численное решение систем линейных алгебраических уравнений (СЛАУ) Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Основное свойство дроби
Основное свойство дроби Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Презентация по математике "Среднее арифметическое" - скачать бесплатно
Презентация по математике "Среднее арифметическое" - скачать бесплатно Презентация на тему Состав чисел от 1 до 10
Презентация на тему Состав чисел от 1 до 10