Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 1 семестр
Содержание
- 2. Литература Дымков М.П., Конюх А.В., Майоровская С.В., Петрович В.Д., Рабцевич В.А. Высшая математика (1 семестр): Учебно-методическое
- 6. Тема 1: Элементы линейной алгебры §1. Матрицы
- 7. Понятие матрицы и основанный на нем раздел математики – матричная алгебра имеют важное значение для экономистов,
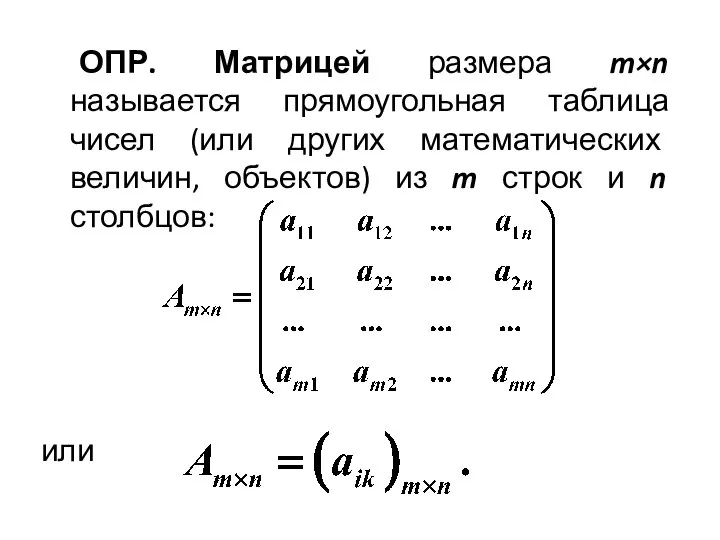
- 8. ОПР. Матрицей размера m×n называется прямоугольная таблица чисел (или других математических величин, объектов) из m строк
- 9. Числа, образующие матрицу, называются элементами матрицы: – элемент, принадлежащий i-й строке и k-му столбцу матрицы, числа
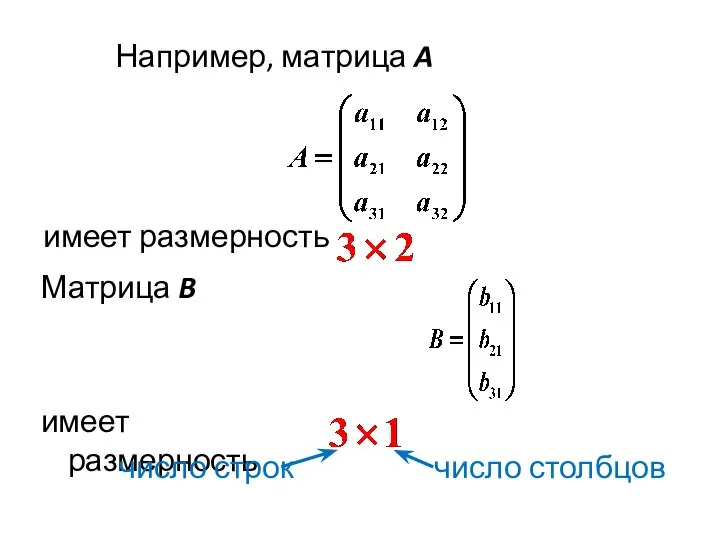
- 10. Например, матрица A имеет размерность Матрица B имеет размерность число строк число столбцов
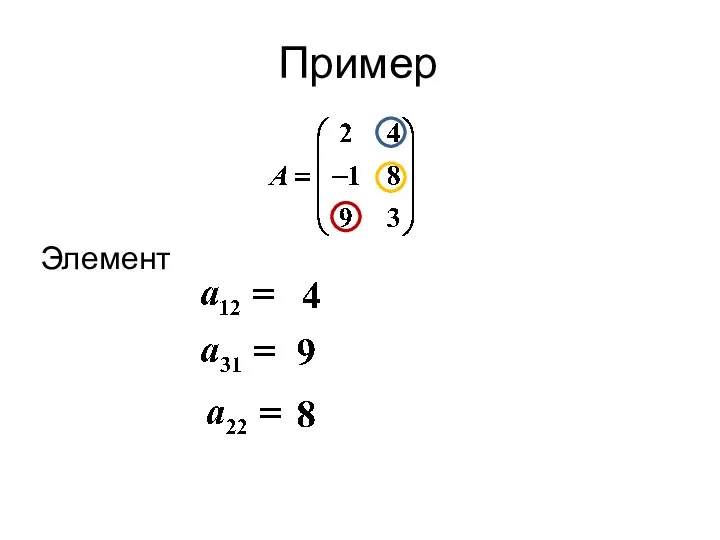
- 11. Пример Элемент
- 12. ОПР. Матрицы A и B одинаковых размеров называются равными, если равны их соответствующие элементы: ОПР. Матрица,
- 13. Пример Дано: Указать размерность данных матриц. Имеются ли среди данных матриц равные?
- 14. ОПР. Квадратной матрицей n-го порядка называется матрица размера n×n. Обозначается В квадратной матрице элементы образуют главную
- 15. Матрица размерности m×1 называется матрицей-столбцом. Матрица размерности 1×n называется матрицей-строкой. Пример.
- 16. ОПР. Квадратная матрица называется диагональной, если ее элементы на главной диагонали не все равны нулю, а
- 17. 1.2. Операции над матрицами К линейным операциям над матрицами относятся сложение и вычитание матриц, умножение матрицы
- 18. ОПР. Суммой (разностью) двух матриц и называется такая матрица что т. е. матрица, элементы которой равны
- 19. Пример Найти A+B, A+C, B+C, если это возможно. Существует сумма B+C:
- 20. ОПР. Произведением матрицы на число (или числа на матрицу A) называется матрица , для которой т.
- 21. Пример
- 22. ОПР. Произведением матриц и называется матрица C размера такая, что т. е. элемент i-й строки и
- 23. Операция умножения двух матриц определяется только для случая, когда число столбцов первой матрицы равно числу строк
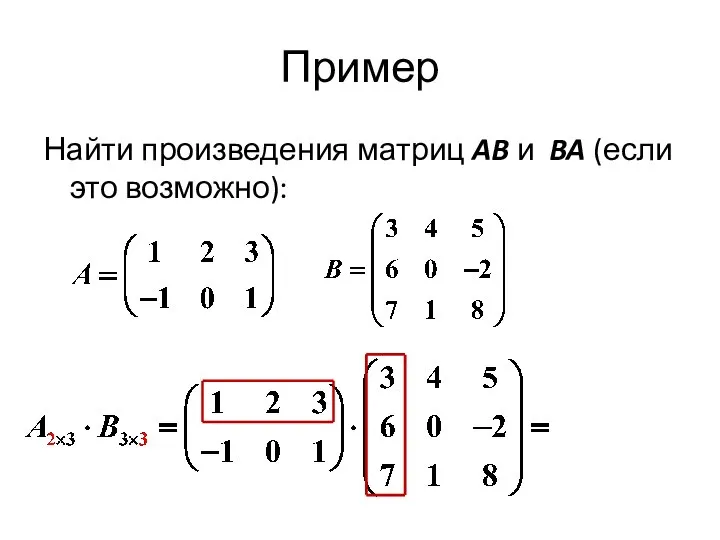
- 24. Пример Найти произведения матриц AB и BA (если это возможно):
- 25. Пример Найти произведения матриц AB и BA (если это возможно):
- 26. Произведение не существует, так как число столбцов матрицы B не совпадает с числом строк матрицы A
- 27. ОПР. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей,
- 28. Свойства
- 29. Элементарные преобразования матриц Перестановка местами двух рядов матрицы; Умножение всех элементов ряда матрицы на число, отличное
- 30. ОПР. Две матрицы A и B называются эквивалентными, если одна из них получается из другой с
- 31. §2. Определители Любой квадратной матрице n-го порядка A можно поставить в соответствие число, которое называется определителем
- 32. Определителем квадратной матрицы 2-го порядка называется число, равное обозначаемое символом
- 33. Пример Вычислить определитель 1. 2.
- 34. Определителем квадратной матрицы 3-го порядка называется число
- 35. Пример Вычислить определитель: Решение.
- 36. ОПР. Минором элемента квадратной матрицы A n-го порядка называется определитель (n-1)-го порядка, полученный из исходного путем
- 37. Пример В матрице минором элемента является минором элемента является Алгебраическое дополнение элемента
- 38. §3. Обратная матрица Пусть A — квадратная матрица n-го порядка. ОПР. Квадратная матрица A называется невырожденной,
- 39. ОПР. Матрицей, присоединенной к матрице называется матрица где — алгебраическое дополнение элемента данной матрицы A. Матрица
- 40. Матрица имеет те же размеры, что и матрица A. Теорема 1. Всякая невырожденная матрица имеет обратную
- 41. Алгоритм вычисления обратной матрицы 1. Находим определитель исходной матрицы. Если , то матрица A вырожденная и
- 42. 3. Находим алгебраические дополнения элементов транспонированной матрицы и из них составляем присоединенную матрицу 4. Вычисляем обратную
- 43. Пример Вычислить обратную матрицу для матрицы Решение. Найдем определитель: Обратная матрица существует.
- 44. Присоединенная матрица имеет вид: Тогда обратная матрица:
- 45. Проверка:
- 46. §4. Матричные уравнения Матричные уравнения простейшего вида с неизвестной матрицей X записываются следующим образом В этих
- 47. Если в уравнениях матрица A невырожденная, то их решения записываются следующим образом Если то Если то
- 48. Пример Решить матричное уравнение: Решение. Запишем данное матричное уравнение в виде . Его решением является матрица
- 49. Значит, обратная матрица существует, и исходное уравнение имеет единственное решение. Запишем решение уравнения:
- 50. Ранг матрицы Рассмотрим матрицу размера m×n. Выделим в ней k строк и k столбцов, Из элементов,
- 52. Скачать презентацию






















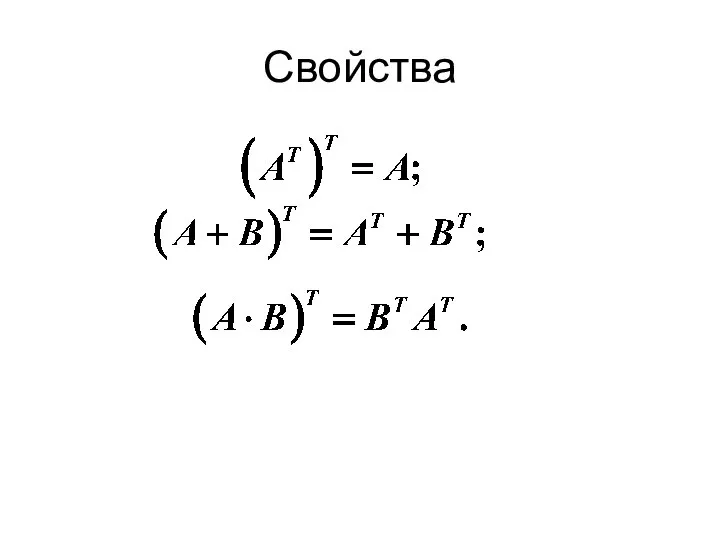
















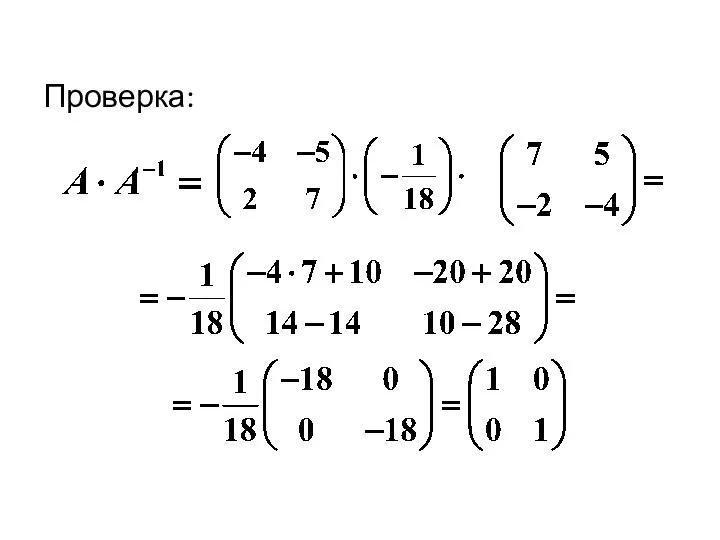





 Математическая задача. Сказка о драконе
Математическая задача. Сказка о драконе Противоположные числа. Устный счет
Противоположные числа. Устный счет Основные тригонометрические формулы
Основные тригонометрические формулы Двугранный угол
Двугранный угол Геометрические места точек. 9 класс
Геометрические места точек. 9 класс Теория графов
Теория графов Теорія двоїстості та аналіз лінійних оптимізаційних задач
Теорія двоїстості та аналіз лінійних оптимізаційних задач Задачи на смеси и сплавы
Задачи на смеси и сплавы Аликвота. Действия с аликвотами
Аликвота. Действия с аликвотами Логарифмы. Показательные и логарифмические уравнения и неравенства (обобщающий урок)
Логарифмы. Показательные и логарифмические уравнения и неравенства (обобщающий урок) Комбинаторные задачи
Комбинаторные задачи Комплексные числа
Комплексные числа Подобие треугольников
Подобие треугольников Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Уравнение и его корни 7 класс. Учитель Козлова Нина Анатольевна, МОУ гимназия №6 г. Красноармейска
Уравнение и его корни 7 класс. Учитель Козлова Нина Анатольевна, МОУ гимназия №6 г. Красноармейска  Обыкновенные дроби. Правила сравнения дробей
Обыкновенные дроби. Правила сравнения дробей Презентация по математике ВЕЛИКИЕ МАТЕМАТИКИ
Презентация по математике ВЕЛИКИЕ МАТЕМАТИКИ  Случайные величины и функции распределения (лекция 1)
Случайные величины и функции распределения (лекция 1) Золотое сечение в архитектуре, скульптуре и живописи
Золотое сечение в архитектуре, скульптуре и живописи Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (3)
Урок систематизации и обобщения знаний, умений и навыков за курс математики 5 – 9 классов (3) Типичные законы распределения вероятностей. Нормальное распределение. Показательное распределение. Равномерное распределение
Типичные законы распределения вероятностей. Нормальное распределение. Показательное распределение. Равномерное распределение Устный счет
Устный счет Своя игра. Готовимся к ОГЭ
Своя игра. Готовимся к ОГЭ Математика вокруг нас
Математика вокруг нас Задачи на чертежах по теме трапеция
Задачи на чертежах по теме трапеция Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно. Теорема. (Семинар 8)
Производная сложной функции. Производная обратной функции. Производная функции, заданной неявно. Теорема. (Семинар 8) Теорема Дезарга
Теорема Дезарга Тренажёр. Табличное умножение и деление. Сложение и вычитание. Поиграем, посчитаем. 2-3 классы
Тренажёр. Табличное умножение и деление. Сложение и вычитание. Поиграем, посчитаем. 2-3 классы