Основные тригонометрические формулы

Август 6, 2022

Главная
Математика
Основные тригонометрические формулы

Содержание

2. Знаки синуса, косинуса и тангенса 1. Знаки синуса и косинуса. Пусть точка (1;0) движется по единичной
3. Зависимость между синусом, косинусом и тангенсом одного и того же угла - основное тригонометрическое тождество. Из
4. Синус, косинус и тангенс углов и Пусть точки М1 и М2 единичной окружности получены поворотом точки
5. Формулы сложения Теорема. Для любых и справедливо равенство
6. Синус, косинус и тангенс двойного угла Выведем формулы синуса и косинуса двойного угла, используя формулы сложения.
7. Синус, косинус и тангенс половинного угла По известным значениям и можно найти значения и , если
9. Скачать презентацию

Слайд 2

Знаки синуса, косинуса и тангенса
1. Знаки синуса и косинуса. Пусть точка

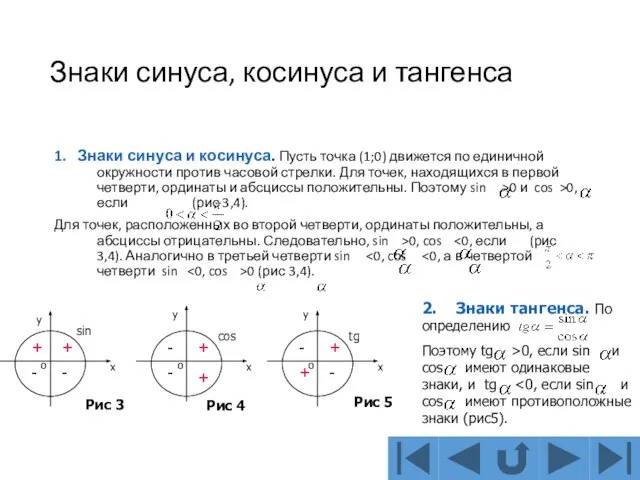
(1;0) движется по единичной окружности против часовой стрелки. Для точек, находящихся в первой четверти, ординаты и абсциссы положительны. Поэтому sin >0 и cos >0, если (рис 3,4).
Для точек, расположенных во второй четверти, ординаты положительны, а абсциссы отрицательны. Следовательно, sin >0, cos <0, если (рис 3,4). Аналогично в третьей четверти sin <0, cos <0, а в четвертой четверти sin <0, cos >0 (рис 3,4).

2. Знаки тангенса. По определению
Поэтому tg >0, если sin и cos имеют одинаковые знаки, и tg <0, если sin и cos имеют противоположные знаки (рис5).

Слайд 3

Зависимость между синусом, косинусом и тангенсом одного и того же угла

- основное тригонометрическое тождество.
Из него можно выразить sin через cos и cos через sin :
В этих формулах знак перед корнем определяется знаком выражения, стоящего в левой части формулы.
Выясним теперь зависимость между тангенсом и котангенсом. По
определению тангенса и котангенса
Перемножая эти равенства, получаем .
Из этого равенства можно выразить tg через ctg и наоборот:

Слайд 4

Синус, косинус и тангенс углов и
Пусть точки М1 и М2 единичной

окружности получены поворотом точки Р(1;0) на углы и соответственно (рис 6). Тогда ось 0х делит угол М10М2 пополам, и поэтому точки М1 и М2 симметричны относительно оси 0х.
Абсциссы этих точек совпадают, а ординаты отличаются только знаками. Точка М1 имеет координаты ( ), точка М2 имеет координаты .
Следовательно,
Используя определение тангенса, получаем .
Таким образом,

Слайд 5

Формулы сложения
Теорема. Для любых и справедливо равенство

Слайд 6

Синус, косинус и тангенс двойного угла
Выведем формулы синуса и косинуса двойного

угла, используя формулы сложения.

1.
Итак,

2.
Итак,

Полагая в формуле получаем

Слайд 7

Синус, косинус и тангенс половинного угла
По известным значениям и можно найти

значения и , если известно, в какой четверти лежит угол .
Из формулы при получаем (1)
Запишем основное тригонометрическое тождество в виде (2)
Складывая равенства (1) и (2) и вычитая из равенства (2) равенство (1), получаем (3)
(4)
Формулы (3) и (4) можно записать так: (5)
(6)
Разделив равенство (6) на равенство (5), получим формулу тангенса половинного угла