Содержание
- 2. Основные задачи и темы курса Цели и задачи курса «Математические методы обработки гидрологической информации» Случайные величины
- 3. Случайные величины Большое число факторов, влияющих на гидрологические характеристики – одно из обоснований для обработки гидрологических
- 4. Закон распределения случайной величины Закон распределения СВ задан, если: указано множество возможных значений СВ указан способ
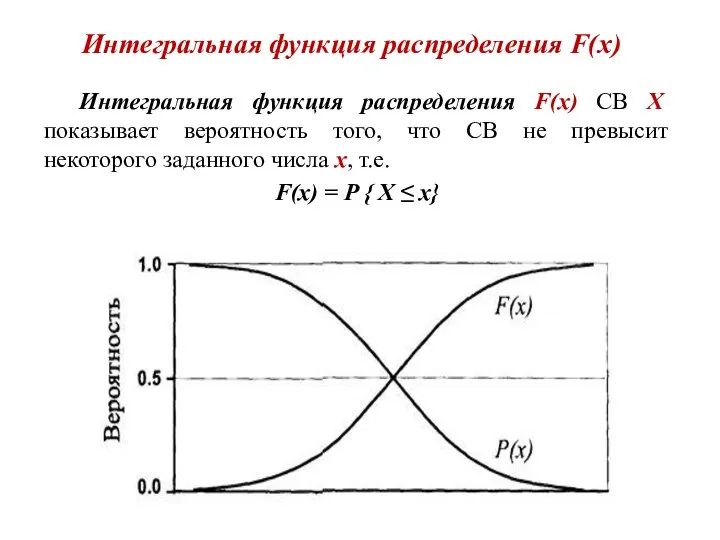
- 5. Интегральная функция распределения F(x) Интегральная функция распределения F(x) СВ X показывает вероятность того, что СВ не
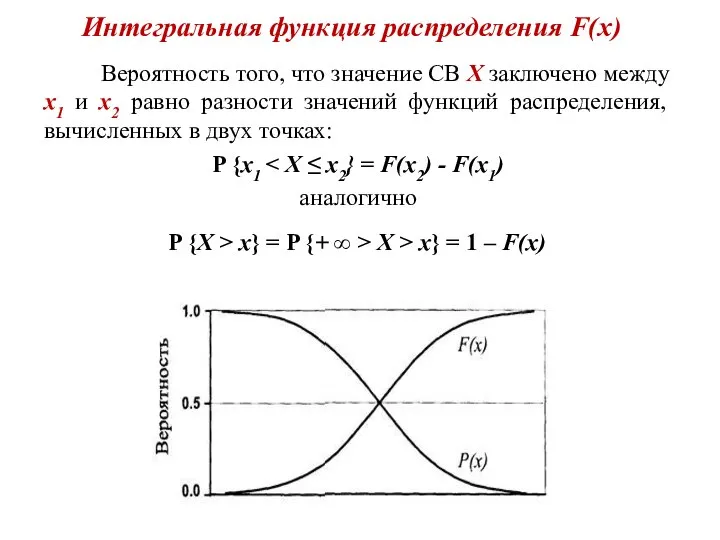
- 6. Интегральная функция распределения F(x) Вероятность того, что значение СВ Х заключено между х1 и х2 равно
- 7. Функция обеспеченности P(х) В гидрологической практике вместо функции F(x) часто используется функция обеспеченности P(х), но с
- 8. Свойства интегральной функции распределения F(x) и функция обеспеченности P(х)
- 9. Дифференциальная функция распределения вероятностей Если функция распределения F(x) дифференцируема для всех значений СВ Х, то закон
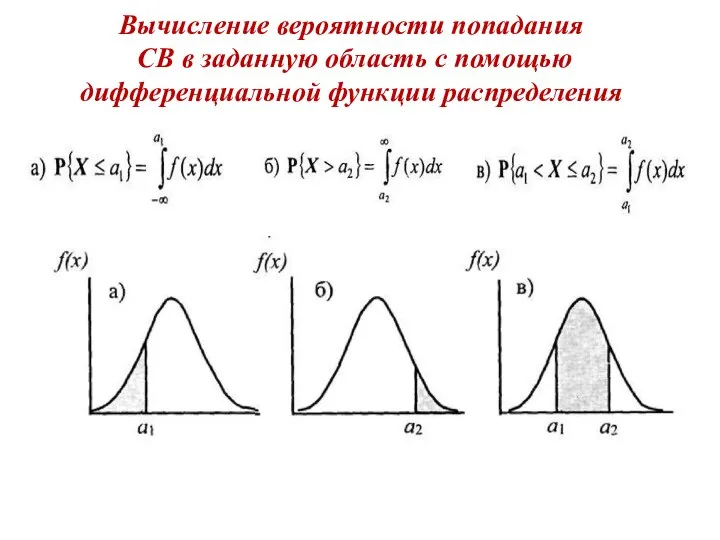
- 10. Свойства функции плотности вероятности f(x) С помощью дифференциальной функции распределения можно вычислить вероятность попадания СВ с
- 11. Вычисление вероятности попадания СВ в заданную область с помощью дифференциальной функции распределения
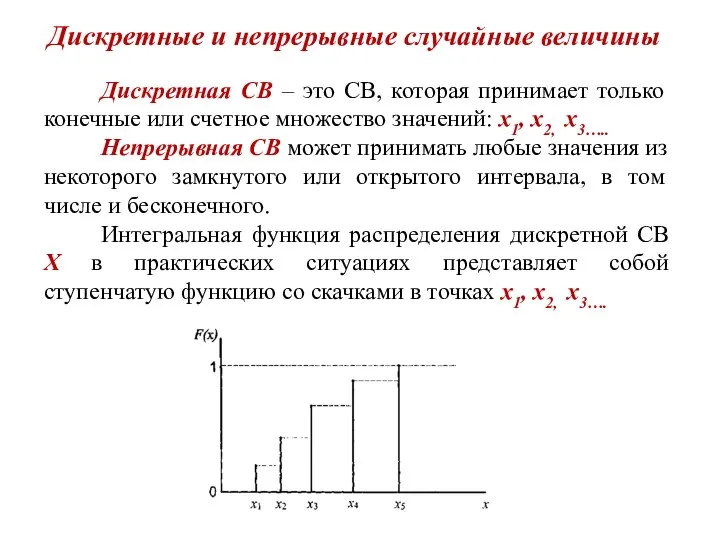
- 12. Дискретные и непрерывные случайные величины Дискретная СВ – это СВ, которая принимает только конечные или счетное
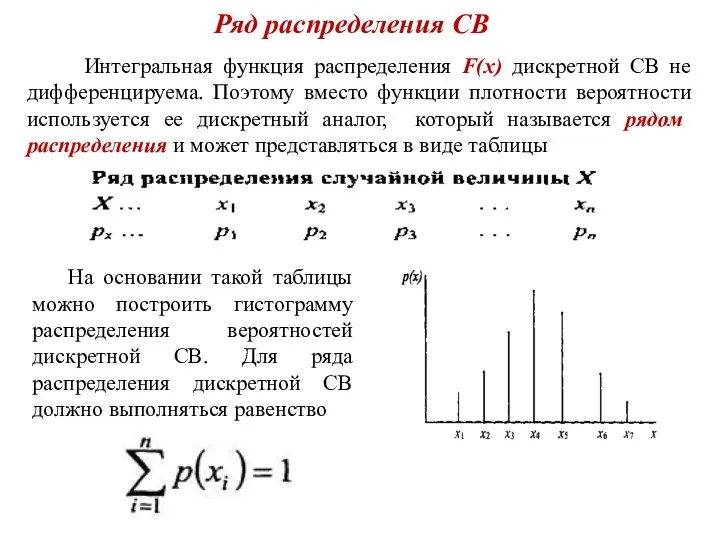
- 13. Ряд распределения СВ Интегральная функция распределения F(x) дискретной СВ не дифференцируема. Поэтому вместо функции плотности вероятности
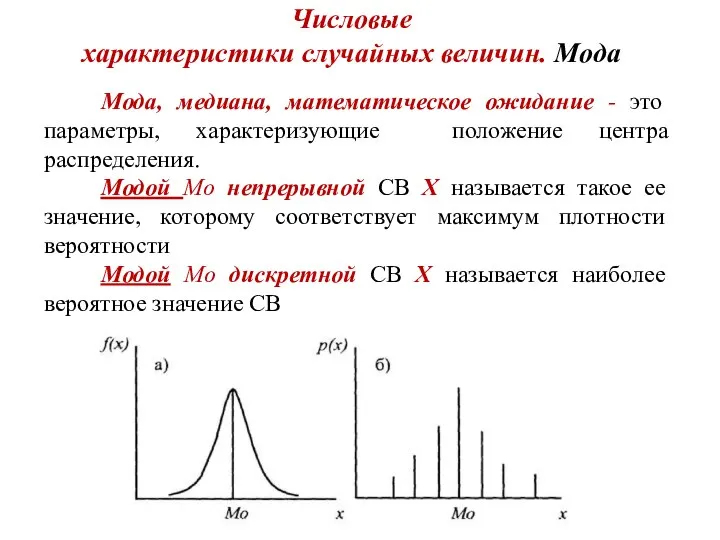
- 14. Числовые характеристики случайных величин. Мода Мода, медиана, математическое ожидание - это параметры, характеризующие положение центра распределения.
- 15. Медиана Медианой Ме непрерывной СВ Х называется такое ее значение, при котором Можно сказать, что Ме
- 16. Математическое ожидание (МО) Математическое ожидание (МО) СВ определяется следующими формулами МО можно трактовать как центр тяжести
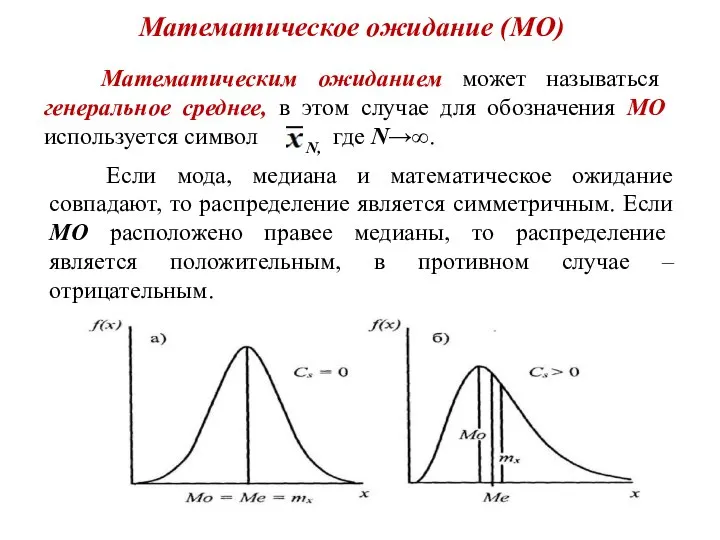
- 17. Математическое ожидание (МО) Математическим ожиданием может называться генеральное среднее, в этом случае для обозначения МО используется
- 18. Моменты случайной величины Различают начальные и центральные моменты СВ Начальный момент S – го порядка СВ
- 19. Дисперсия Вторую группу наиболее часто используемых на практике параметров составляют параметры, характеризующие степень рассеяния СВ относительно
- 20. Среднеквадратичное отклонение Коэффициент вариации Среднеквадратичное отклонение (СКО) СВ Х (стандарт) это квадратный корень из дисперсии. Для
- 21. Асимметрия Коэффициент асимметрии С является безразмерным параметром и характеризует степень симметричности рассеяния относительно математического ожидания. Коэффициент
- 22. Эксцесс Эксцесс Ех также является безразмерным параметром и определяется формулой Эксцесс позволяет оценить островершинность, или наоборот
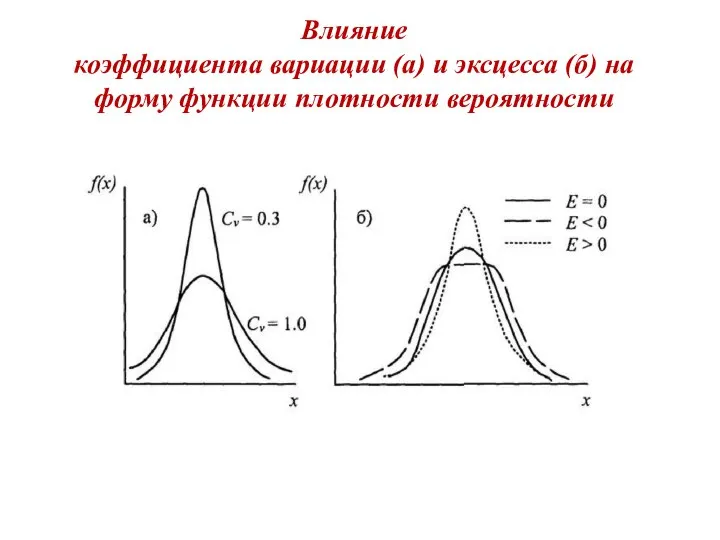
- 23. Влияние коэффициента вариации (а) и эксцесса (б) на форму функции плотности вероятности
- 24. Свойства математического ожидания 1. МО постоянной величины равно самой этой величине: М[c] = c, где с
- 25. Свойства дисперсии Дисперсия постоянной величины равно нулю D[c] = 0, где с = const. 2. Постоянную
- 26. Стандартные преобразования случайных величин. В гидрологической практике наиболее часто используется замена СВ Х модульными коэффициентами и
- 27. Квантили распределения Во многих практических случаях необходимо по заданной вероятности не превышения F(x) = p’ определить
- 29. Скачать презентацию















![Свойства дисперсии Дисперсия постоянной величины равно нулю D[c] = 0, где](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1467598/slide-24.jpg)


 Таблица умножения и деления на 4
Таблица умножения и деления на 4 Работа ученицы 7 класса Г МОУ «СОШ № 24»г. Северодвинска Лысковской Татьяны Учитель математики Паршева В.В.
Работа ученицы 7 класса Г МОУ «СОШ № 24»г. Северодвинска Лысковской Татьяны Учитель математики Паршева В.В. Финансовая математика в задачах ЕГЭ и практической деятельности человека
Финансовая математика в задачах ЕГЭ и практической деятельности человека Классическая линейная модель множественной регрессии. Лекция 2
Классическая линейная модель множественной регрессии. Лекция 2 Метод координат. Решение задач
Метод координат. Решение задач Презентация по математике "Рациональные числа" - скачать бесплатно
Презентация по математике "Рациональные числа" - скачать бесплатно Вводное повторение. 7 класс
Вводное повторение. 7 класс Решение квадратных неравенств
Решение квадратных неравенств Решение логарифмических уравнений и неравенств
Решение логарифмических уравнений и неравенств Параллельный перенос
Параллельный перенос Презентация по математике "Решаем задачи и примеры. 2класс" - скачать
Презентация по математике "Решаем задачи и примеры. 2класс" - скачать  Умножение натуральных чисел и их свойства
Умножение натуральных чисел и их свойства Буйство красок, звуков, рифм смиряет циркуль, логарифм
Буйство красок, звуков, рифм смиряет циркуль, логарифм Измерения. Прямое измерение. Косвенное измерение
Измерения. Прямое измерение. Косвенное измерение Parallelepiped rectangular solid cube. Some special prisms
Parallelepiped rectangular solid cube. Some special prisms Метод Монте-Карло
Метод Монте-Карло Разложение на множители. Суммы и разности кубов
Разложение на множители. Суммы и разности кубов Аттестационная работа. Рабочая программа внеурочной деятельности «За страницами учебника математики». (5 класс)
Аттестационная работа. Рабочая программа внеурочной деятельности «За страницами учебника математики». (5 класс) Части графа. Операции над частями графа
Части графа. Операции над частями графа Презентация по математике "Переместительное свойство сложения" - скачать бесплатно
Презентация по математике "Переместительное свойство сложения" - скачать бесплатно Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Прямоугольный параллелепипед
Прямоугольный параллелепипед Урок 3. Случайное событие. Классическое, статистическое и геометрическое определение вероятности
Урок 3. Случайное событие. Классическое, статистическое и геометрическое определение вероятности Презентация на тему Решение задач 1 класс
Презентация на тему Решение задач 1 класс  Правило вычисления значения алгебраической суммы двух чисел
Правило вычисления значения алгебраической суммы двух чисел Смежные и вертикальные углы
Смежные и вертикальные углы Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат
Четырехугольники: параллелограмм, трапеция, прямоугольник, ромб, квадрат Теорема Чевы
Теорема Чевы