Содержание
- 2. Однією з центральних задач логіки є аналіз міркувань. Міркування являє собою ланцюг тверджень, кожне з яких
- 3. На практиці відношення логічного слідування часто застосовують не до формул, а до висловлень, сформульованих в природній
- 4. Теорема. Формула В логічно слідує з посилок А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ...,
- 5. Доведення “тільки тоді”. Дано: А1, А2, ..., Аm╞ В. (1) Довести: А1∧А2∧... ∧Аm⇒В ≡ 1. (2)
- 6. Властивості логічного слідування (випливають з означення і доведеної теореми): якщо А1, А2, ..., Аm╞ В1, В1╞
- 7. Схеми логічного слідування: А⇒В, А ╞ В – modus ponens (МР). (ponens – що стверджує) Для
- 8. Теорема. А≡В тоді і тільки тоді, коли ╞А⇔В. Користуючись поняттям дкнф можна розв’язати задачу знаходження всіх
- 9. З питанням про логічне слідування тісно пов’язане питання про сумісність чи несумісність (суперечливість) множини висловлень. Означення.
- 11. Скачать презентацию
Слайд 2
Однією з центральних задач логіки є аналіз міркувань. Міркування являє собою
Однією з центральних задач логіки є аналіз міркувань. Міркування являє собою
ланцюг тверджень, кожне з яких є або вихідним, або слідує із встановлених раніше тверджень.
Нехай задані формули алгебри висловлень А і В, з яких хоча б одна містить пропозиційні букви р1, р2, ..., рn.
Означення. Говорять, що формула В слідує логічно з формули А (на базі алгебри висловлень), якщо В набуває значення 1 при кожному розподілі істиннісних значень р1, р2, ..., рn, при якому А має значення 1. При цьому А називається посилкою, припущенням або гіпотезою, а В – логічним висновком.
Означення. Говорять, що формула В слідує логічно з формул А1, А2, ..., Аm, якщо В набуває значення 1 при кожному такому розподілі істинісних значень р1, р2, ..., рn, при якому всі посилки А1, А2, ..., Аm, мають значення 1. Позначають: А1, А2, ..., Аm╞ В.
Нехай задані формули алгебри висловлень А і В, з яких хоча б одна містить пропозиційні букви р1, р2, ..., рn.
Означення. Говорять, що формула В слідує логічно з формули А (на базі алгебри висловлень), якщо В набуває значення 1 при кожному розподілі істиннісних значень р1, р2, ..., рn, при якому А має значення 1. При цьому А називається посилкою, припущенням або гіпотезою, а В – логічним висновком.
Означення. Говорять, що формула В слідує логічно з формул А1, А2, ..., Аm, якщо В набуває значення 1 при кожному такому розподілі істинісних значень р1, р2, ..., рn, при якому всі посилки А1, А2, ..., Аm, мають значення 1. Позначають: А1, А2, ..., Аm╞ В.
Слайд 3
На практиці відношення логічного слідування часто застосовують не до формул, а
На практиці відношення логічного слідування часто застосовують не до формул, а
до висловлень, сформульованих в природній мові.
Означення. Нехай Х1, Х2, ..., Хm, У – висловлення, А1, А2, ..., Аm, В – відповідно їх логічні структури. Говорять, що висловлення У логічно слідує з висловлень Х1, Х2, ..., Хm, (на базі логіки висловлень) тоді і тільки тоді, коли формула алгебри висловлень В логічно слідує з формул А1, А2, ..., Аm (на базі алгебри висловлень).
Дані означення дають алгоритм перевірки логічного слідування даної формули з формул-посилок тільки у випадку, коли для цих формул задано їх таблиці істинності. Тому значно зменшується можливість безпосереднього практичного застосування цих означень.
Означення. Нехай Х1, Х2, ..., Хm, У – висловлення, А1, А2, ..., Аm, В – відповідно їх логічні структури. Говорять, що висловлення У логічно слідує з висловлень Х1, Х2, ..., Хm, (на базі логіки висловлень) тоді і тільки тоді, коли формула алгебри висловлень В логічно слідує з формул А1, А2, ..., Аm (на базі алгебри висловлень).
Дані означення дають алгоритм перевірки логічного слідування даної формули з формул-посилок тільки у випадку, коли для цих формул задано їх таблиці істинності. Тому значно зменшується можливість безпосереднього практичного застосування цих означень.
Слайд 4
Теорема. Формула В логічно слідує з посилок А1(р1, р2, ..., рn),
Теорема. Формула В логічно слідує з посилок А1(р1, р2, ..., рn),
А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn) (на базі алгебри висловлень) тоді і тільки тоді, коли формула
А1(р1, р2, ..., рn)∧А2(р1, р2, ..., рn)∧... ∧Аm(р1, р2, ..., рn)⇒В є тавтологією.
Доведення “тоді”.
Дано: А1∧А2∧... ∧Аm⇒В ≡ 1.
Довести: А1, А2, ..., Аm╞ В.
Розглянемо довільний розподіл істинісних значень р1, р2, ..., рn, при якому всі Аі (і=1, ..., m) набувають значення 1. Тоді │А1∧А2∧...∧Аm│=1 на розглядуваному наборі значень р1, р2, ..., рn. Значення В на цьому наборі не може бути нулем, бо за означенням імплікації ми б мали:
│А1∧А2∧... ∧Аm⇒В│= 0 на розглядуваному наборі.
А це суперечить умові. Отже, на довільному наборі р1, р2, ..., рn, де всі посилки Аі (і=1, ..., m) набувають значення 1, │В│= 1. Отже, за означенням В логічно слідує з посилок А1, А2, ..., Аm.
А1(р1, р2, ..., рn)∧А2(р1, р2, ..., рn)∧... ∧Аm(р1, р2, ..., рn)⇒В є тавтологією.
Доведення “тоді”.
Дано: А1∧А2∧... ∧Аm⇒В ≡ 1.
Довести: А1, А2, ..., Аm╞ В.
Розглянемо довільний розподіл істинісних значень р1, р2, ..., рn, при якому всі Аі (і=1, ..., m) набувають значення 1. Тоді │А1∧А2∧...∧Аm│=1 на розглядуваному наборі значень р1, р2, ..., рn. Значення В на цьому наборі не може бути нулем, бо за означенням імплікації ми б мали:
│А1∧А2∧... ∧Аm⇒В│= 0 на розглядуваному наборі.
А це суперечить умові. Отже, на довільному наборі р1, р2, ..., рn, де всі посилки Аі (і=1, ..., m) набувають значення 1, │В│= 1. Отже, за означенням В логічно слідує з посилок А1, А2, ..., Аm.
Слайд 5
Доведення “тільки тоді”.
Дано: А1, А2, ..., Аm╞ В. (1)
Довести: А1∧А2∧... ∧Аm⇒В ≡
Доведення “тільки тоді”.
Дано: А1, А2, ..., Аm╞ В. (1)
Довести: А1∧А2∧... ∧Аm⇒В ≡
1. (2)
Припустимо, що (2) не є тавтологією. Тоді знайдеться хоча б один такий набір значень р1, р2, ..., рn, на якому:
│А1∧А2∧... ∧Аm⇒В│= 0.
На цьому наборі за означенням імплікації маємо:
│А1∧А2∧...∧Аm│=1, (3)
│В│= 0. (4)
З рівності (3) слідує, що всі Аі (і=1, ..., m) на цьому наборі мають значення 1. Враховуючи це і рівність (4) маємо, що В не слідує логічно з А1, А2, ..., Аm.
Отже, ми отримали суперечність з (1). Наше припущення неправильне. Т.д.
Припустимо, що (2) не є тавтологією. Тоді знайдеться хоча б один такий набір значень р1, р2, ..., рn, на якому:
│А1∧А2∧... ∧Аm⇒В│= 0.
На цьому наборі за означенням імплікації маємо:
│А1∧А2∧...∧Аm│=1, (3)
│В│= 0. (4)
З рівності (3) слідує, що всі Аі (і=1, ..., m) на цьому наборі мають значення 1. Враховуючи це і рівність (4) маємо, що В не слідує логічно з А1, А2, ..., Аm.
Отже, ми отримали суперечність з (1). Наше припущення неправильне. Т.д.
Слайд 6
Властивості логічного слідування (випливають з означення і доведеної теореми):
якщо А1, А2,
Властивості логічного слідування (випливають з означення і доведеної теореми):
якщо А1, А2,
..., Аm╞ В1, В1╞ В2,
то А1, А2, ..., Аm╞ В2 (транзитивність);
якщо А1, А2, ..., Аm╞ В, А – довільна формула алгебри висловлень, то
А1, А2, ..., Аm, А╞ В
(приєднання довільної формули алгебри висловлень до числа посилок не порушує даного логічного слідування);
якщо А1, А2, ..., Аі-1, Аі, Аі+1, ..., Аm╞ В і ╞Аі,
то А1, А2, ..., Аі-1, Аі+1, ..., Аm╞ В
(вилучення з числа посилок формули, яка є тавтологією, не порушує даного логічного слідування).
то А1, А2, ..., Аm╞ В2 (транзитивність);
якщо А1, А2, ..., Аm╞ В, А – довільна формула алгебри висловлень, то
А1, А2, ..., Аm, А╞ В
(приєднання довільної формули алгебри висловлень до числа посилок не порушує даного логічного слідування);
якщо А1, А2, ..., Аі-1, Аі, Аі+1, ..., Аm╞ В і ╞Аі,
то А1, А2, ..., Аі-1, Аі+1, ..., Аm╞ В
(вилучення з числа посилок формули, яка є тавтологією, не порушує даного логічного слідування).
Слайд 7
Схеми логічного слідування:
А⇒В, А ╞ В – modus ponens (МР). (ponens
Схеми логічного слідування:
А⇒В, А ╞ В – modus ponens (МР). (ponens
– що стверджує)
Для доведення потрібно показати, що (А⇒В )∧ А ⇒ В – тавтологія.
А⇒В, ⎤В╞ ⎤А – modus tollens (МT). (tollens – заперечувальний)
А∧В╞А, А∧В╞В – правило вилучення кон’юнкції, ОК (опускання кон’юнкції)
А╞А∨В, В╞А∨В – правило введення диз’юнкції, ВД
А1⇒А2, А2⇒А3 ╞ А1⇒А3 – правило силогізму
А, В╞ А∧В – правило введення кон’юнкції, ВК
А1⇒А3, А2⇒А3 ╞ А1∨А2⇒А3 – правило вилучення диз’юнкції, ОД
Для доведення потрібно показати, що (А⇒В )∧ А ⇒ В – тавтологія.
А⇒В, ⎤В╞ ⎤А – modus tollens (МT). (tollens – заперечувальний)
А∧В╞А, А∧В╞В – правило вилучення кон’юнкції, ОК (опускання кон’юнкції)
А╞А∨В, В╞А∨В – правило введення диз’юнкції, ВД
А1⇒А2, А2⇒А3 ╞ А1⇒А3 – правило силогізму
А, В╞ А∧В – правило введення кон’юнкції, ВК
А1⇒А3, А2⇒А3 ╞ А1∨А2⇒А3 – правило вилучення диз’юнкції, ОД
Слайд 8
Теорема. А≡В тоді і тільки тоді, коли ╞А⇔В.
Користуючись поняттям дкнф можна
Теорема. А≡В тоді і тільки тоді, коли ╞А⇔В.
Користуючись поняттям дкнф можна
розв’язати задачу знаходження всіх можливих логічних висновків, які можна зробити з даних посилань.
Нехай формули А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn)– посилання. З’єднаємо ці посилання знаком ∧ і формулу, що при цьому одержиться, зведемо до Дкнф. Якщо тепер вибрати довільні кон’юнктивні члени по одному і по два тощо і з’єднати їх знаком ∧, то всі вирази, що при цьому одержаться, і тільки вони будуть логічними висновками з даних посилань.
Обернена задача: знайти посилання, для яких дана формула є логічним висновком. Для цього дану формулу зводимо до дкнф знаходимо ті конституенти одиниці, які відсутні в даній формулі, і беремо різні кон’юнкції даної формули і цих конституент.
Нехай формули А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn)– посилання. З’єднаємо ці посилання знаком ∧ і формулу, що при цьому одержиться, зведемо до Дкнф. Якщо тепер вибрати довільні кон’юнктивні члени по одному і по два тощо і з’єднати їх знаком ∧, то всі вирази, що при цьому одержаться, і тільки вони будуть логічними висновками з даних посилань.
Обернена задача: знайти посилання, для яких дана формула є логічним висновком. Для цього дану формулу зводимо до дкнф знаходимо ті конституенти одиниці, які відсутні в даній формулі, і беремо різні кон’юнкції даної формули і цих конституент.
Слайд 9
З питанням про логічне слідування тісно пов’язане питання про сумісність чи
З питанням про логічне слідування тісно пов’язане питання про сумісність чи
несумісність (суперечливість) множини висловлень.
Означення. Множина формул Г = {А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn)} називається сумісною (несуперечною), якщо існує такий розподіл істинісних значень р1, р2, ..., рn, при якому:
│А1(р1, р2, ..., рn)∧А2(р1, р2, ..., рn) ∧ ... ∧ Аm(р1, р2, ..., рn)│=1.
Множина формул, яка не є сумісною, називається суперечною.
Твердження. Множина формул алгебри висловлень Г = {А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn)} є сумісною (суперечною) тоді і тільки тоді, коли хоча б на одному наборі (на всіх наборах) значень р1, р2, ..., рn всі формули (хоча б одна з формул) Аі (і=1, 2, ..., m) набувають (набуває) значення 1 (0).
Дослідження сумісності чи суперечності даної множини формул алгебри висловлень можна проводити методом відшукання контрприкладу.
Означення. Множина формул Г = {А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn)} називається сумісною (несуперечною), якщо існує такий розподіл істинісних значень р1, р2, ..., рn, при якому:
│А1(р1, р2, ..., рn)∧А2(р1, р2, ..., рn) ∧ ... ∧ Аm(р1, р2, ..., рn)│=1.
Множина формул, яка не є сумісною, називається суперечною.
Твердження. Множина формул алгебри висловлень Г = {А1(р1, р2, ..., рn), А2(р1, р2, ..., рn), ..., Аm(р1, р2, ..., рn)} є сумісною (суперечною) тоді і тільки тоді, коли хоча б на одному наборі (на всіх наборах) значень р1, р2, ..., рn всі формули (хоча б одна з формул) Аі (і=1, 2, ..., m) набувають (набуває) значення 1 (0).
Дослідження сумісності чи суперечності даної множини формул алгебри висловлень можна проводити методом відшукання контрприкладу.
- Предыдущая
Кетчуп и ПельмениСледующая -
Физические упражнения для детей с ОНР







 тема_реклама_правила_разимещения_и_взаимодействие_реклама+фотографновая
тема_реклама_правила_разимещения_и_взаимодействие_реклама+фотографновая Шаблон к совещанию. Обзор бизнеса по картингу за календарную неделю
Шаблон к совещанию. Обзор бизнеса по картингу за календарную неделю Металлургические базы России
Металлургические базы России Моя семья
Моя семья Әлеуметтік желілердің қазіргі жастардың дүниетанымына тигізетін әсері
Әлеуметтік желілердің қазіргі жастардың дүниетанымына тигізетін әсері Веселые ребята Космическое путешествие
Веселые ребята Космическое путешествие Токарные станки
Токарные станки Электронные замки
Электронные замки Украшающие швы
Украшающие швы Открытка для мамы
Открытка для мамы Др. Восток
Др. Восток 1 Лiтературна норма
1 Лiтературна норма Современная библиотека от идеи до создания бренда
Современная библиотека от идеи до создания бренда Инструменты для обработки отверстий. Часть 1
Инструменты для обработки отверстий. Часть 1 КАК СШИТЬ МАСКУ
КАК СШИТЬ МАСКУ Гигиена певческого голоса
Гигиена певческого голоса Железнодорожный транспорт и перевозка грузов
Железнодорожный транспорт и перевозка грузов FORWARD 5. UNIT 4. ON THE OIL RIG
FORWARD 5. UNIT 4. ON THE OIL RIG Спортивный калейдоскоп
Спортивный калейдоскоп 20141211_prezentatsiya_metod_proektov_v_prepodavanii
20141211_prezentatsiya_metod_proektov_v_prepodavanii The XV International Forum-Contest of Students and Young Researchers
The XV International Forum-Contest of Students and Young Researchers Строение древесины, ее свойства, пороки. Раскрой хлыстов на сортименты, их сортировка и окорка
Строение древесины, ее свойства, пороки. Раскрой хлыстов на сортименты, их сортировка и окорка Идеология терроризма
Идеология терроризма Технологии искусственного интеллекта
Технологии искусственного интеллекта Бакулева Достижения химии
Бакулева Достижения химии Accelerated aging diseases and their genetic causes Complex pattern of aging markers in primary human fibroblasts
Accelerated aging diseases and their genetic causes Complex pattern of aging markers in primary human fibroblasts Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint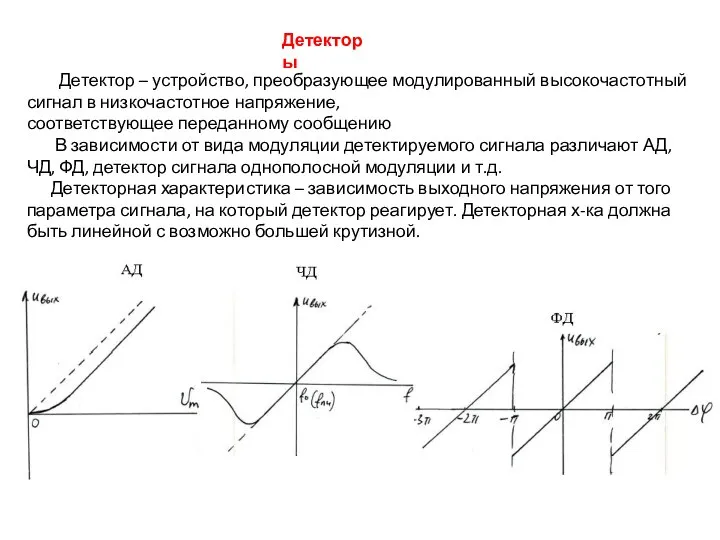 Детекторы. Детекторная характеристика
Детекторы. Детекторная характеристика