Модели каналов передачи информации при наличии помех. Математическое описание канала передачи информации

Модели каналов передачи информации при наличии помех

Учебные вопросы
Математическое описание канала связи.
Взаимная

Литература

 1.Вернер М. Основы кодирования − М.: Техносфера, 2004. – 288 с.

Цели передачи по каналу с шумом

1. Быстрое кодирование информации.
2. Простой способ

Статистические (стохастические) каналы

Переходная вероятность
p(y(t)|x(t)),
показывает, с какой вероятностью фиксированный входной

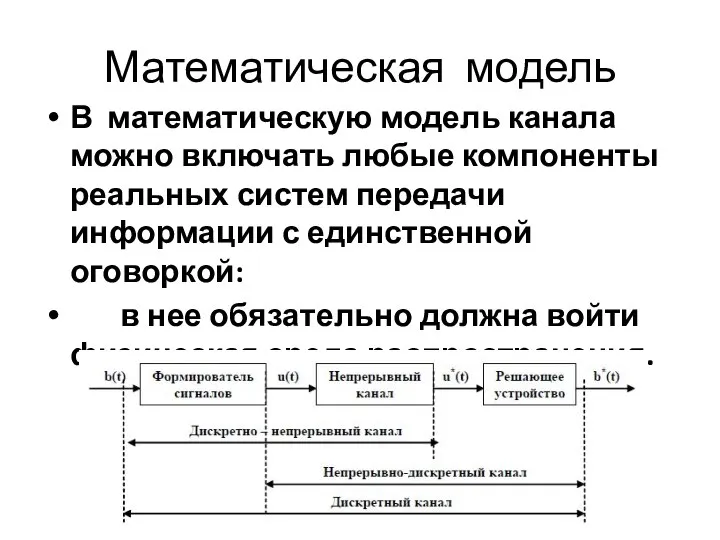
Математическая модель

В математическую модель канала можно включать любые компоненты реальных

Классификация каналов:

Дискретные и непрерывные как по времени, так и по

Классификация каналов:

Канал называется дискретным по состоянию, если входное и выходное

Канал без памяти
Отклик на входное воздействие не зависит от значения

Дискретный канал без памяти (ДКБП)

Пусть x(i), y(i) – входные и выходные

ДКБП

ДКБП полностью описывается своей символьной или мгновенной переходной вероятностью p(y(i)|x(i)), которая

Пример. Двоичный симметричный канал (ДСК):

p – вероятность ошибки на символ.

Симметричный q-ичный канал:

Канал по которому передается q-ичное слово с независимыми

Канал со стираниями (стирающий)

Переходная матрица

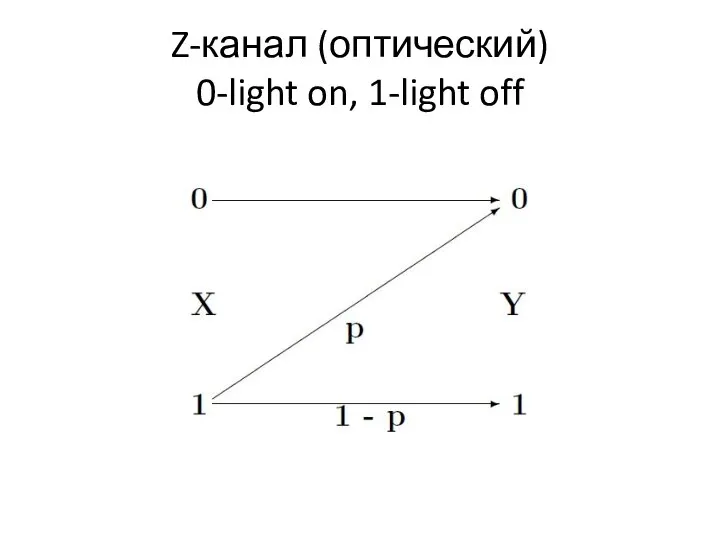
Z-канал (оптический) 0-light on, 1-light off

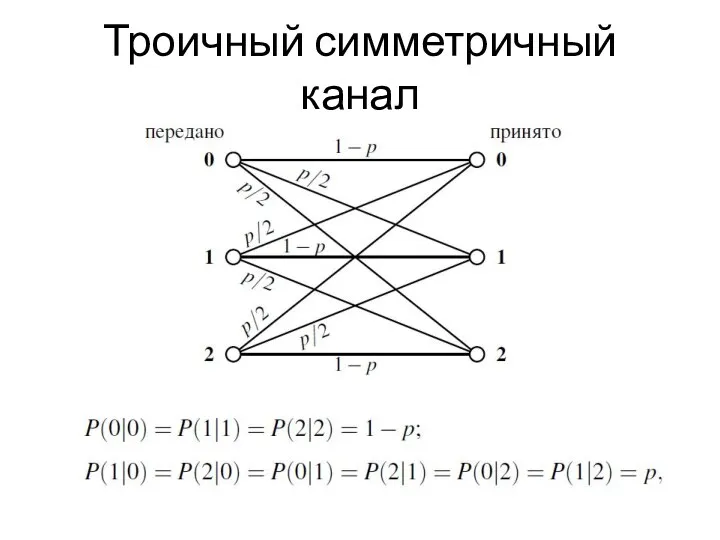
Троичный симметричный канал

Двоичные каналы связи

Модели
Гильберта,
Эллиота-Гильберта,
Смита-Боуэна-Джойса и
Фричмана-Свободы.
Первые три модели используют

А. А. Марков

Математик,
академик,
внёсший большой
вклад в
теорию вероятностей
математический анализ
теорию чисел

Цепи Маркова

A. Марков (1856-1922)

Пример. Цепи Маркова

Пример. Цепи Маркова

Вычислим P(W через 2 дня)?

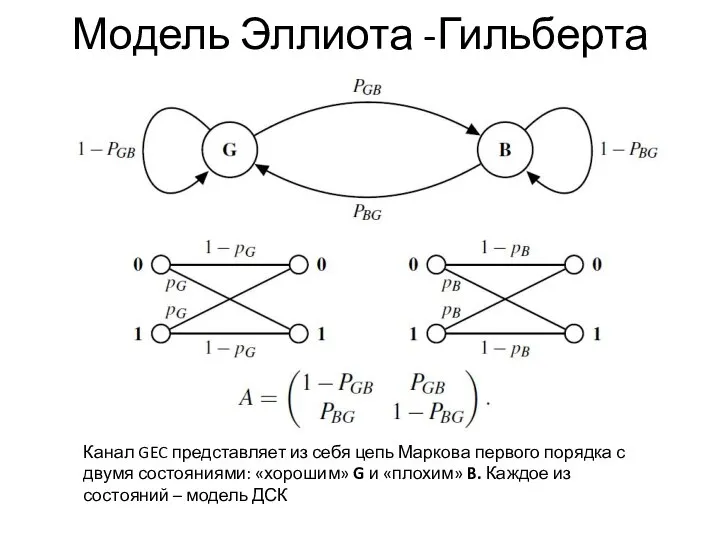
Модель Эллиота -Гильберта

Канал GEC представляет из себя цепь Маркова первого порядка

Апостериорная вероятность

Полная информация, которую можно извлечь из y об x,

Условная энтропия H(X|y)

Неопределенность множества возможных значений входа x, вычисленной при фиксированном

Остаточная энтропия

Усреднение H(X|y) по всем возможным y, дает численную меру

Средняя взаимная информация

Полагая p(y)p(x|y)=p(x,y), получим
Снижение неопределенности после наблюдения y выразится в

Средняя взаимная информация

I(X;Y) показывает число битов информации о входе канала извлекаемое

Взаимная информация

Взаимная информация между x и y.
Здесь первое слагаемое правой

Пропускная способность

Максимальное количество информации, которое можно в принципе передать по

Пропускная способность

Пропускная способность – фундаментальный параметр канала, определяющий его потенциальные

Р. Фано

Неравенство Фано (лемма),
связывающего среднюю потерю информации в канале передачи

Ошибка декодирования (ошибочное решение). Неравенство Фано

Вероятность ошибки декодирования Pe
Вероятность правильного решения

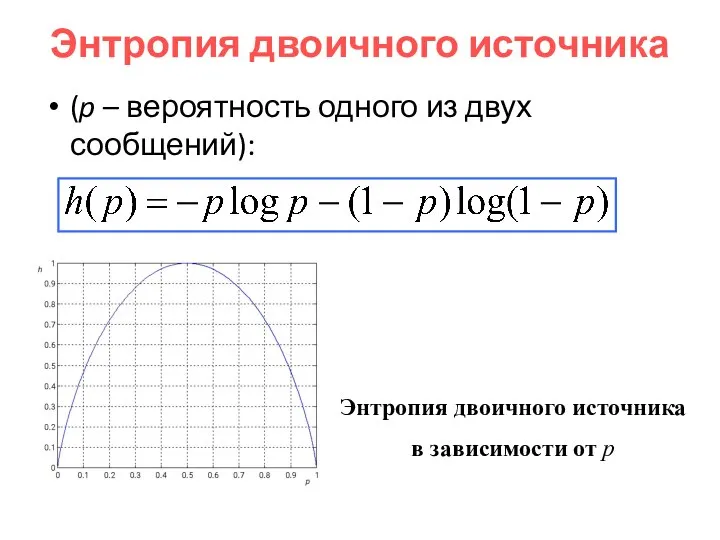
Неравенство Фано

Остаточная энтропия и вероятность ошибки декодирования
где h(·) – энтропия

Энтропия двоичного источника

(p – вероятность одного из двух сообщений):

Энтропия двоичного

Скорость передачи или скорость кода R
Пусть одно из M равновероятных сообщений,

Теоремы Шеннона

Обратная теорема кодирования

При скорости, превышающей пропускную способность канала, R>C, не существует

Прямая теорема кодирования

При скорости, меньшей пропускной способности канала, R

Случайное кодирование

В среднем по всем возможным кодам вероятность ошибочного декодирования ограничена

Случайное кодирование

Верхняя граница для Pe (экспонента случайного кодирования) является экспоненциально точной,

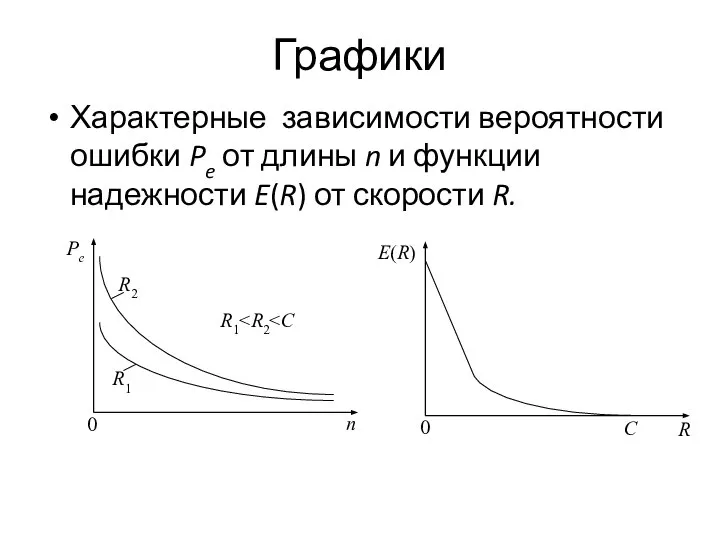
Графики

Характерные зависимости вероятности ошибки Pe от длины n и функции надежности

Задача ТК

Прямая теорема Шеннона является типичной математической теоремой существования, не давая

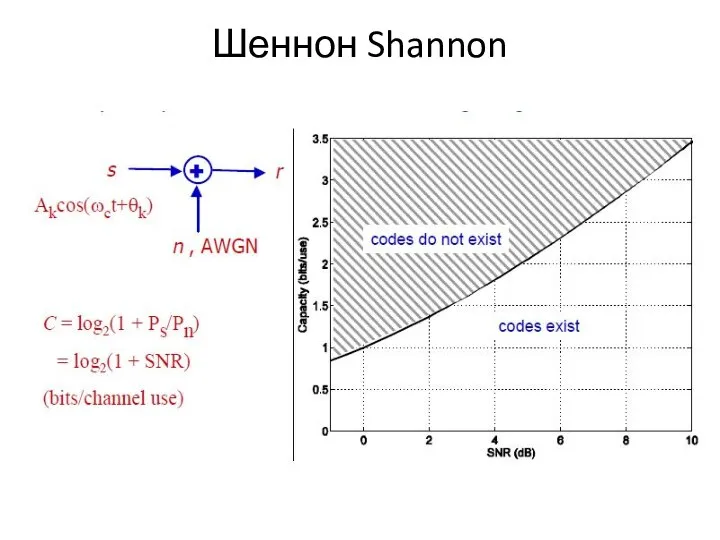
Шеннон. Гауссовский канал с аддитивным шумом

Шеннон Shannon

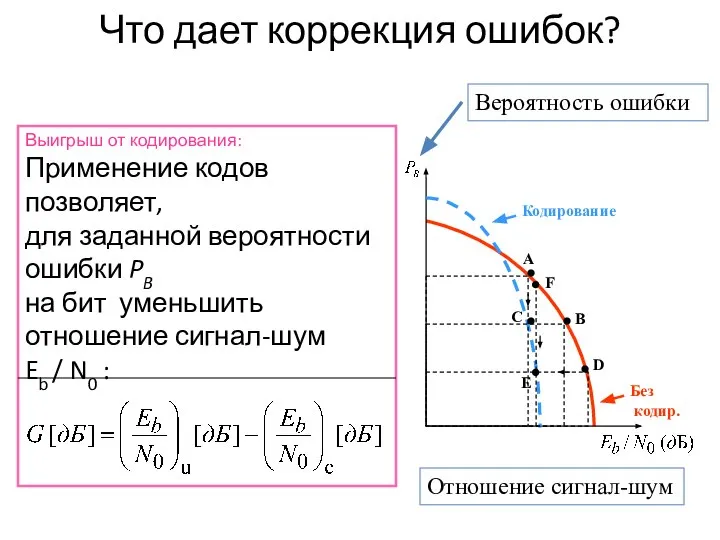
Что дает коррекция ошибок?

Выигрыш от кодирования:
Применение кодов позволяет,
для заданной вероятности